《剑指offer》(7)动态规划、回溯
class Solution:
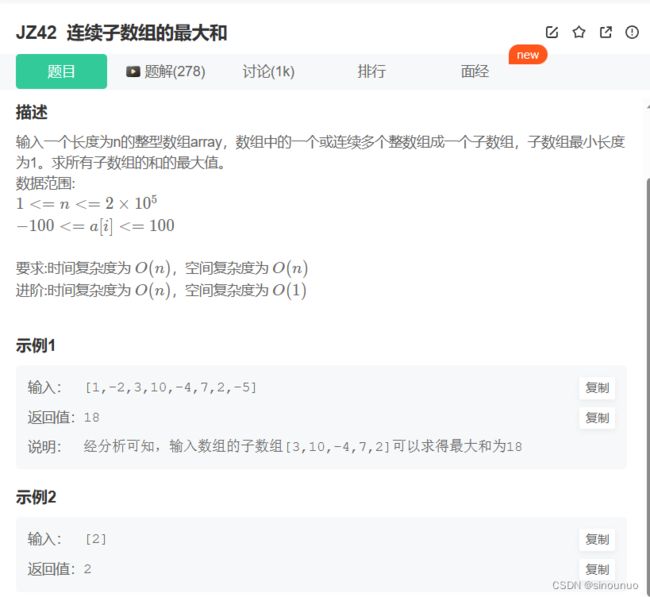
def FindGreatestSumOfSubArray(self , array: List[int]) -> int:
if len(array) <= 1:
return array[0]
n = len(array)
dp = [0]*n
dp[0] = array[0]
for i in range(1,n):
dp[i] = max(array[i],dp[i-1]+array[i])
return max(dp)
class Solution:
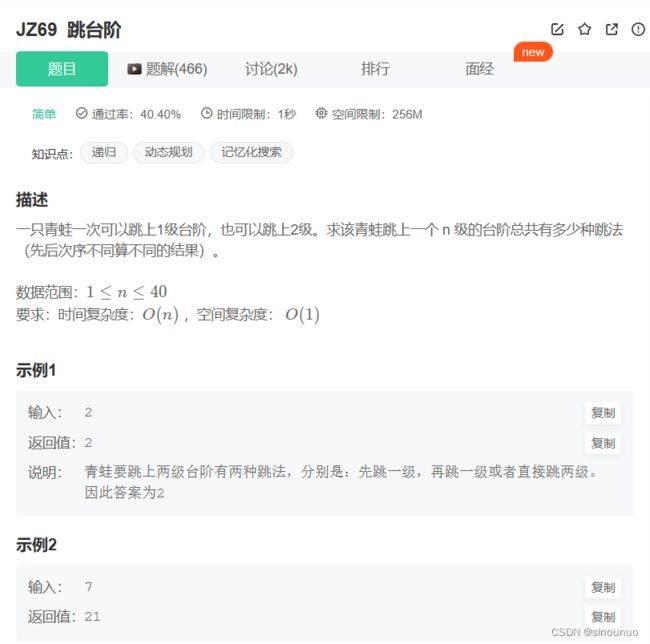
def jumpFloor(self , number: int) -> int:
#f[n] = f[n-1] + f[n-2] ,要么从倒数第二级跳上来,要么从倒数第一个跳上来
f0,f1 = 1,1
for i in range(2,number+1):
f1,f0 = f1+f0,f1
return f1
class Solution:
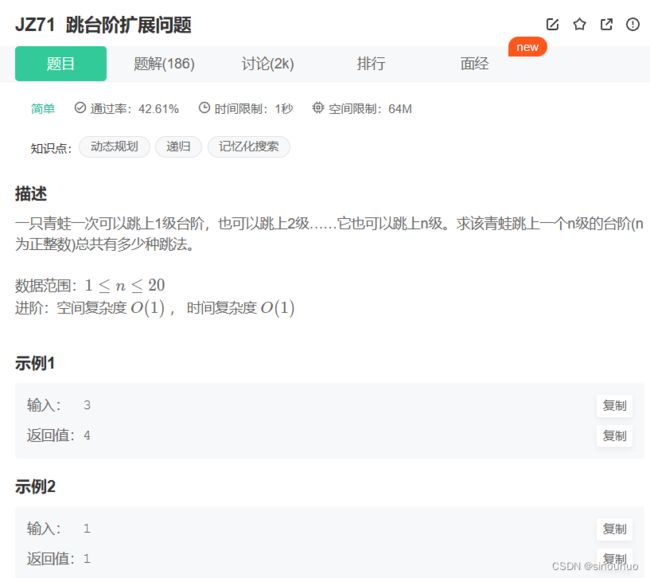
def jumpFloorII(self , number: int) -> int:
#f[n] = f[n-1]+f[n-2]+f[n-3]+...+f[0]
if number <= 1:
return number
f = [1]
for i in range(1,number+1):
a = sum(f)
f.append(a)
return f[-1]
class Solution:
def Fibonacci(self , n: int) -> int:
if n <= 2:
return 1
f0,f1 = 1,1
for i in range(3,n+1):
f1,f0 = f1+f0,f1
return f1
class Solution:
def maxProfit(self , prices: List[int]) -> int:
#dp[i][0] 今天不持股,是昨天持股的最大值+卖出股票的prices[i] or 昨天也不持股的值
#dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
#dp[i][1] 今天持股,昨天持股的值dp[i-1][1], or 昨天不持股今天持股 -prices[i]
#dp[i][1] = max(dp[i - 1][1], -prices[i]);
#只能买卖一次
n = len(prices)
if n <= 1:
return 0
dp = []
dp.append([0,-prices[0]]) #dp[0][0] = 0,dp[0][1]=-prices[0]
for i in range(1,n):
dp.append([max(dp[i-1][0],dp[i-1][1]+prices[i]),max(dp[i-1][1],-prices[i])])
#返回最后一天不持股的情况
return dp[n-1][0]
思路:使用左右指针同向移动,并且使用dp数组 记录当前的最大和,如果出现了新的最大和,或者区间增加,就修改start,end指针,最后输出start到end+1的范围即可。
class Solution:
def FindGreatestSumOfSubArray(self , array: List[int]) -> List[int]:
if len(array) <= 1:
return array
n = len(array)
dp = [0]*n
dp[0] = array[0]
maxsum = dp[0]
left,right = 0,1
start,end = 0,0
while right < n:
dp[right] = max(dp[right-1]+array[right],array[right]) #计算当前的dp最大和
if dp[right-1]+array[right] < array[right]: #如果和小于当前值,那移动左指针
left = right
if maxsum < dp[right] or maxsum == dp[right] and (right-left) > (end-start): #出现新的最大值或者区间,更新区间和最大和。
maxsum = dp[right]
start = left
end = right
right += 1
return array[start:end+1]
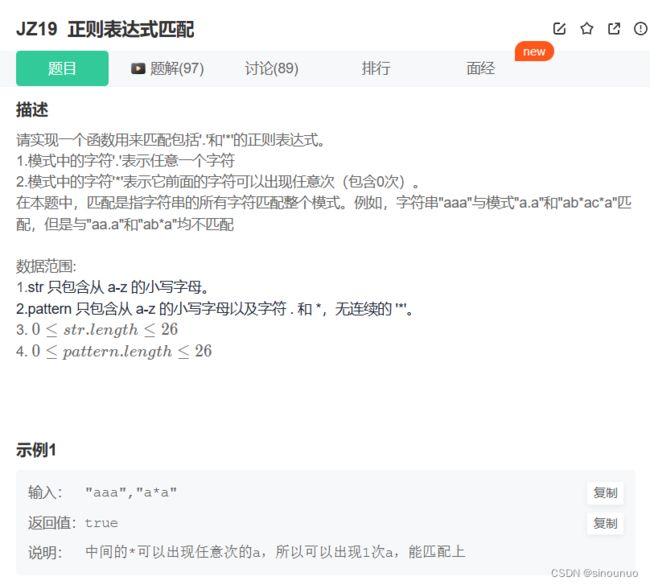
思路:递归
class Solution:
def match(self , s: str, pattern: str) -> bool:
if not pattern: return not s #特殊情况,不存在匹配模式,递归出口
first_match = s and pattern[0] in {s[0],'.'} #首位匹配
if len(pattern) >= 2 and pattern[1] == '*':
return (self.match(s,pattern[2:]) or first_match and self.match(s[1:],pattern)) #两种情况,要么首位匹配并且s[1:]之后和pattern匹配,要么s和pattern[2:]匹配
else:
return first_match and self.match(s[1:],pattern[1:]) #否则依次匹配之后的情况
class Solution:
def rectCover(self, number):
#递归,n=1,结果是1,n=2,结果是2,n=3,结果是3,n=4,结果是5
#f(n) = f(n-1)+f(n-2)
if number <= 1:
return number
f0,f1 = 1,1
for i in range(2,number+1):
f0,f1 = f1,f0+f1
return f1
思路:当前格子的最大值一定是max(左边最大值+当前值,右边最大值+当前值)
class Solution:
def maxValue(self , grid: List[List[int]]) -> int:
n = len(grid)
if n <= 0:
return 0
m = len(grid[0])
if m <= 0:
return 0
dp = [[0]*(m+1) for _ in range(n+1)]
maxsum = 0
for i in range(1,n+1):
for j in range(1,m+1):
dp[i][j] = max(dp[i-1][j]+grid[i-1][j-1],dp[i][j-1]+grid[i-1][j-1])
if maxsum < dp[i][j]:
maxsum = dp[i][j]
return maxsum
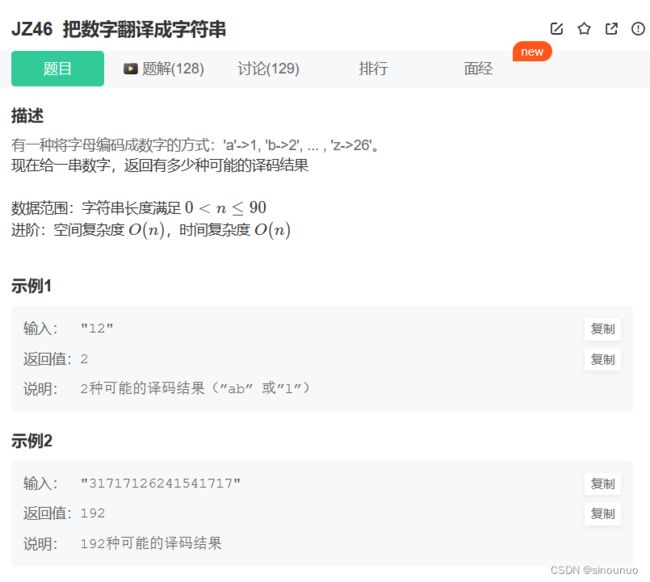
class Solution:
def solve(self , nums: str) -> int:
f = [1]*(len(nums)+1)
if int(nums) == 0: #处理所有的特殊情况,nums不能是0
return 0
elif int(nums) == 10 or int(nums) == 20: #如果nums是10或者20
return 1
else:
for i in range(1,len(nums)):
if nums[i] == '0'and (nums[i-1] != '1' and nums[i-1] !='2'):
return 0 #如果有一个数是0,前面既不是2也不是1,那就无法转换
for i in range(len(nums)): #其余正常情况
if i < 1 :
f[i+1] = f[i] *1
else:
if 10 < int(nums[i-1:i+1]) < 20 or 20 < int(nums[i-1:i+1]) < 27:#不要10和20
f[i+1] = f[i-1] + f[i]
else:
f[i+1] = f[i] * 1
return f[-1]
思路:双指针,每次不出现重复,就更新长度,出现了重复就缩小左边的窗口。
class Solution:
def lengthOfLongestSubstring(self , s: str) -> int:
left,right = 0,1
maxlen = 0
if len(s) <= 1:
return len(s)
while right < len(s):
if s[right] not in s[left:right]:
maxlen = max(right-left+1,maxlen)
right += 1
else:
left += 1
return maxlen
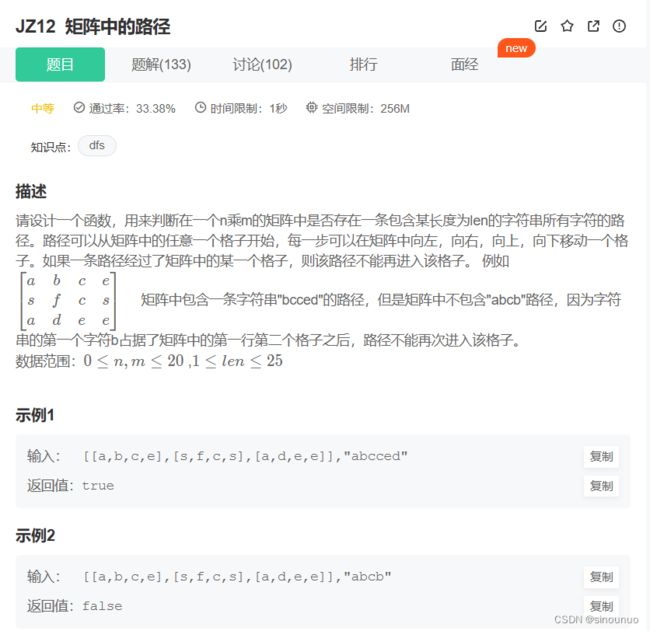
思路:回溯就是一条一条的去找路,首先是大框架一定会遍历二维数组,然后遍历到每一个节点都去找路径,如果找到了,就返回True,在最后返回Falsr(因为之前肯定没找到)。主要是招路径的dfs方法,想象成一颗4叉树,如果当前i,j越界或者不匹配路径,返回false,如果走到了路径尾就返回ture,然后递归找上下左右的路。!!!为了保证走过的不能再走,所以走之前我们要修改当前值为'.',等递归之后再改回来。
class Solution:
def dfs(self,matrix,word,i,j,index):
#如果越界或者不等于当前路径
if i >= len(matrix) or i < 0 or j >= len(matrix[0]) or j < 0 or matrix[i][j] != word[index]:
return False
#到达路径最后
if index == len(word) - 1:
return True
#保存当前值,为了不重复要修改当前值
temp = matrix[i][j]
matrix[i][j] = '.'
#上下左右找路
res = self.dfs(matrix,word,i-1,j,index+1) or self.dfs(matrix,word,i+1,j,index+1) or self.dfs(matrix,word,i,j-1,index+1) or self.dfs(matrix,word,i,j+1,index+1)
#恢复当前值
matrix[i][j] = temp
return res
def hasPath(self , matrix: List[List[str]], word: str) -> bool:
n = len(matrix)
m = len(matrix[0])
if m > 0 and n > 0:
for i in range(n):
for j in range(m):
if self.dfs(matrix,word,i,j,0):
return True
return False
思路:从(0,0)开始找上下左右可以去的格子,如果越界或者这个格子来过或者格子不满足条件,都返回0,否则就标注格子可达(将对应位置置位1),然后返回1+上下左右的和。
class Solution:
def movingCount(self , threshold: int, rows: int, cols: int) -> int:
#异常值判断
if rows <=0 or cols <= 0 or threshold < 0:
return 0
#存储该位置是否可达
dp = [[0]*cols for _ in range(rows)]
#各位数之和
def cal(i):
s = 0
while i :
s += i % 10
i //= 10
return s
#找路的递归函数
def dfs(threshold,rows,cols,i,j,dp):
#越界或者已经到过了或者不满足条件
if i < 0 or i >= rows or j < 0 or j >= cols or dp[i][j] or cal(i)+cal(j) > threshold:
return 0
#可达
dp[i][j] = 1
return 1 + dfs(threshold,rows,cols,i+1,j,dp) + dfs(threshold,rows,cols,i-1,j,dp) + dfs(threshold,rows,cols,i,j+1,dp) + dfs(threshold,rows,cols,i,j-1,dp)
res = dfs(threshold,rows,cols,0,0,dp)
return res