数学建模:BP神经网络模型及其优化
文章首发于我的个人博客:欢迎大佬们来逛逛
文章目录
- BP神经网络
-
- 算法流程
- 代码实现
- 神经网络的超参数优化
-
- 代码实现
- 神经网络的分类
BP神经网络
算法流程
设 x 1 , x 2 , . . . , x i x_1,x_2,...,x_i x1,x2,...,xi 为输入变量, y y y 为输出变量, u j u_j uj 为隐藏层神经元的输出, f 为激活函数的映射关系。
设 v i j v_{ij} vij 为第 i i i 个输入变量与第 j j j 个隐藏层神经元的权重。
设 w j w_{j} wj 为第 j j j 个隐藏层神经元与 最终输出结果 y y y 的权重。
- 建立激活函数:常见的有 s i g m o d sigmod sigmod 激活函数,当然还有其他的激活函数,例如 t a n h tanh tanh 函数 与 R e L U ReLU ReLU 函数
s i g m o d 激活函数: f ( x ) = 1 1 + e − x sigmod激活函数:f(x)=\frac1{1+e^{-x}} sigmod激活函数:f(x)=1+e−x1
R e L U 激活函数: f ( x ) = { x i f x > 0 0 i f x < 0 ReLU 激活函数: \begin{aligned}f(x)=&\begin{cases}\mathrm{x}&\mathrm{~if~}x>0\\0&\mathrm{~if~}x<0&\end{cases}{}&\end{aligned} ReLU激活函数:f(x)={x0 if x>0 if x<0
- 进行正向传播,正向传播的公式如下
u j = f ( ∑ i = 1 n ν i j x i + θ j u ) j = 1 , 2 , … , m y = f ( ∑ j = 1 m w j u j + θ y ) \begin{aligned}u_j&=f\big(\sum_{i=1}^n\nu_{ij}x_i+\theta_j^u\big)j=1,2,\ldots,m\\y&=f(\sum_{j=1}^mw_ju_j+\theta^y)\end{aligned} ujy=f(i=1∑nνijxi+θju)j=1,2,…,m=f(j=1∑mwjuj+θy)
- 我们最终想要得到的目标为真实值与通过网络预测值之间误差尽可能小,目标函数设定为:
- 其中真实输出值是 y ^ \hat y y^ ,预测输出值是: y y y,我们希望他们的差值平方求和尽可能小。
J = ∑ k ( y ( k ) − y ^ ( k ) ) 2 J=\sum_k{(y^{(k)}-\hat y^{(k)})^2} J=k∑(y(k)−y^(k))2
b. 改变一下形式,拿出第 k k k 个对象做目标,再把所有对象总和作为最终目标, x i k x_i^{k} xik 代表第i个特征的输入:
J ( k ) = ( y ( k ) − y ^ ( k ) ) 2 J^{(k)}=(y^{(k)}-\hat y^{(k)})^2 J(k)=(y(k)−y^(k))2
- 进行梯度下降法的反向传播,运用链式求导法则。
- 参数的优化:
v i j ′ = v i j − μ ∂ J ∂ v i j w j ′ = w j − μ ∂ J ∂ w j \begin{aligned}v_{ij}^{\prime}&=v_{ij}-\mu\frac{\partial J}{\partial v_{ij}}\\\\w_j^{\prime}&=w_j-\mu\frac{\partial J}{\partial w_j}\end{aligned} vij′wj′=vij−μ∂vij∂J=wj−μ∂wj∂J
- 得到最优参数 v v v 和 w w w 以后,就可以获取模型,然后预测输出。
代码实现
function [ret_y_test_data,ret_BP_predict_data] = mfunc_BPnetwork(data,hiddenLayers,gradientDescentMethods)
% BP神经网络算法
% params:
% data:原始数据,Shape:(m,n) 需要从m行中抽取一部分作为test,剩下的作为train。第n列为预测结果
% hiddenLayers: newff函数所需要做的神经网络模型的隐藏层个数及每层数量,例如:[6,6,6] 三个隐藏层,每层6个数据
% gradientDescentMethods:每个隐藏层所需要的梯度下降算法,需要与hiddenLayers的数量一致,例如:{'logsig','tansig','logsig'};必须使用花括号
% returns:
% ret_y_test_data:实际测试数据
% ret_BP_predict_data:预测数据
[m,n]=size(data);
% 划分训练集与测试集
train_num=round(0.8*m); % 划分数量
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n); % 第n列表表示预测结果
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
% 标准化 mapminmax对行操作,需要转置
x_train_data=x_train_data';
y_train_data=y_train_data';
x_test_data=x_test_data';
% x_train_maxmin与y_train_maxmin用于以后复原
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data,0,1);
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data,0,1);
% 创建网络
t1=clock;
net=newff(x_train_regular,y_train_regular,hiddenLayers,gradientDescentMethods);
% net=newff(x_train_regular,y_train_regular,[6,3,3],{'logsig','tansig','logsig','purelin'});
% net=newff(x_train_regular,y_train_regular,6,{'logsig','logsig'});
% net=newff(x_train_regular,y_train_regular,6,{'logsig','purelin'});
% net=newff(x_train_regular,y_train_regular,6,{'logsig','tansig'});
% %设置训练次数
% net.trainParam.epochs = 50000;
% %设置收敛误差
% net.trainParam.goal=0.000001;
% newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF) takes optional inputs,
% TF- Transfer function of ith layer. Default is 'tansig' for
% hidden layers, and 'purelin' for output layer.
%%激活函数的设置
% compet - Competitive transfer function.
% elliotsig - Elliot sigmoid transfer function.
% hardlim - Positive hard limit transfer function.
% hardlims - Symmetric hard limit transfer function.
% logsig - Logarithmic sigmoid transfer function.
% netinv - Inverse transfer function.
% poslin - Positive linear transfer function.
% purelin - Linear transfer function.
% radbas - Radial basis transfer function.
% radbasn - Radial basis normalized transfer function.
% satlin - Positive saturating linear transfer function.
% satlins - Symmetric saturating linear transfer function.
% softmax - Soft max transfer function.
% tansig - Symmetric sigmoid transfer function.
% tribas - Triangular basis transfer function.
%训练网络
[net,~]=train(net,x_train_regular,y_train_regular);
%%
%将输入数据归一化
% 利用x_train_maxmin来对x_test_data进行标准化
x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
%放入到网络输出数据
y_test_regular=sim(net,x_test_regular);
%将得到的数据反归一化得到预测数据
BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
%%
BP_predict=BP_predict';
errors_nn=sum(abs(BP_predict-y_test_data)./(y_test_data))/length(y_test_data);
t2=clock;
Time_all=etime(t2,t1);
disp(['运行时间:',num2str(Time_all)])
figure;
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
ret_y_test_data = y_test_data;
hold on
plot(BP_predict,'*','Color',color(1,:))
ret_BP_predict_data = BP_predict;
hold on
titlestr=['MATLAB自带newff神经网络',' 误差为:',num2str(errors_nn)];
title(titlestr)
disp(titlestr)
end
神经网络的超参数优化
使用 fitrnet 可以进行神经网络的超参数优化。
具体步骤如下:使用贝叶斯方法进行超参数优化
- OptimizeHyperparameters:auto
- HyperparameterOptimizationOptions:struct(“AcquisitionFunctionName”,“expected-improvement-plus”,‘MaxObjectiveEvaluations’,optimize_num)
- optimize_num:设置一个优化次数
Mdl = fitrnet(x_train_regular,y_train_regular,"OptimizeHyperparameters","auto", ...
"HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus",'MaxObjectiveEvaluations',optimize_num))
其他与上面完全一样
代码实现
function mfunc_BP_OptimizedNetwork(data,optimize_num)
% 神经网络的超参数优化
%
[m,n]=size(data);
train_num=round(0.8*m);
% 获取训练集与测试集
x_train_data=data(1:train_num,1:n-1);
y_train_data=data(1:train_num,n);
x_test_data=data(train_num+1:end,1:n-1);
y_test_data=data(train_num+1:end,n);
% 需要一次转置,mapminmax对行操作,并且返回的是转置后的
[x_train_regular,x_train_maxmin] = mapminmax(x_train_data');
[y_train_regular,y_train_maxmin] = mapminmax(y_train_data');
% 将标准化后的训练集转置回来
x_train_regular=x_train_regular';
y_train_regular=y_train_regular';
% 自定义优化次数
% optimize_num = 5;
% fitrnet 使用贝叶斯方法进行优化
Mdl = fitrnet(x_train_regular,y_train_regular,"OptimizeHyperparameters","auto", ...
"HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus",'MaxObjectiveEvaluations',optimize_num));
% 导入测试集,进行测试集的标准化,同样x_test_data需要转置,并且我们指定它进行与训练集x执行相同的标准化
x_test_regular = mapminmax('apply',x_test_data',x_train_maxmin);
x_test_regular=x_test_regular';
% 数据预测predict:放入到网络输出数据,得到 经过标准化后的预测结果
y_test_regular=predict(Mdl,x_test_regular);
% 将得到的数据反标准化得到真正的预测数据
BP_predict=mapminmax('reverse',y_test_regular,y_train_maxmin);
% 可视化与输出
errors_nn=sum(abs(BP_predict-y_test_data)./(y_test_data))/length(y_test_data);
figure;
color=[111,168,86;128,199,252;112,138,248;184,84,246]/255;
plot(y_test_data,'Color',color(2,:),'LineWidth',1)
hold on
plot(BP_predict,'*','Color',color(1,:))
hold on
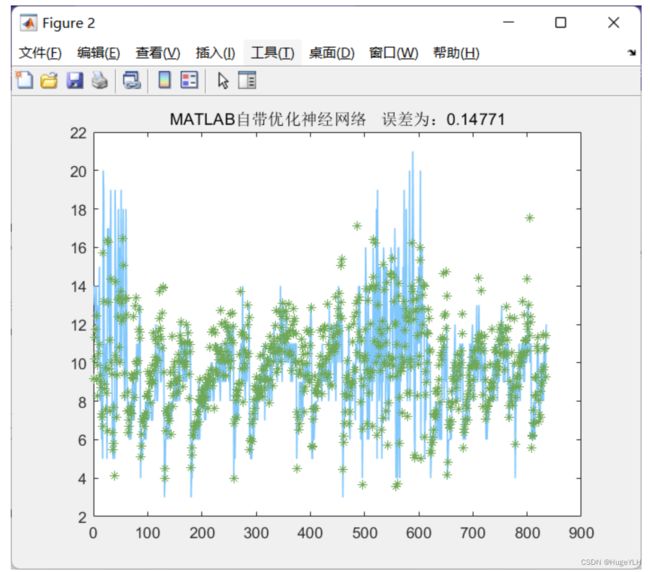
titlestr=['MATLAB自带优化神经网络',' 误差为:',num2str(errors_nn)];
title(titlestr)
disp(titlestr)
end
神经网络的分类
分类问题:输出结果固定为 1,2,3等某一类。
最后可以得到准确率
clc;clear;close all;
load('iri_data.mat')
data=(iri_data);
%% 看数据分布
train_num=round(0.8*size(data,1));%取整个数据0.8的比例训练,其余作为测试数据
choose=randperm(size(data,1));
train_data=data(choose(1:train_num),:);
test_data=data(choose(train_num+1:end),:);
n=size(data,2);
y=train_data(:,n);
x=train_data(:,1:n-1);
optimize_num=5;
% 使用贝叶斯网络进行优化
Mdl = fitcnet(x,y,"OptimizeHyperparameters","auto", ...
"HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus",'MaxObjectiveEvaluations',optimize_num));
%% 测试一下效果
% x_test_regular = mapminmax('apply',x_test_data,x_train_maxmin);
% x_test_regular=x_test_regular';
%放入到网络输出数据
y_test_regular=predict(Mdl,test_data(:,1:end-1));
y_test_ture=test_data(:,end);
%%
accuracy=length(find(y_test_regular==y_test_ture))/length(y_test_ture);
disp('准确率为:')
disp(accuracy)
|============================================================================================================================================|
| Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | Activations | Standardize | Lambda | LayerSizes |
| | result | | runtime | (observed) | (estim.) | | | | |
|============================================================================================================================================|
| 1 | Best | 0.17241 | 1.5495 | 0.17241 | 0.17241 | relu | false | 1.1049e-05 | 1 |
| 2 | Best | 0.068966 | 8.2032 | 0.068966 | 0.073079 | sigmoid | true | 1.7483e-06 | [236 45 2] |
| 3 | Accept | 0.63793 | 0.18258 | 0.068966 | 0.08784 | relu | true | 82.744 | [295 41] |
| 4 | Accept | 0.63793 | 0.097396 | 0.068966 | 0.092718 | none | true | 193.49 | 11 |
| 5 | Best | 0.060345 | 6.157 | 0.060345 | 0.062326 | sigmoid | true | 3.6739e-06 | [211 51 5] |
__________________________________________________________
优化完成。
达到 MaxObjectiveEvaluations 5。
函数计算总次数: 5
总历时: 19.1325 秒
总目标函数计算时间: 16.1897
观测到的最佳可行点:
Activations Standardize Lambda LayerSizes
___________ ___________ __________ _________________
sigmoid true 3.6739e-06 211 51 5
观测到的目标函数值 = 0.060345
估计的目标函数值 = 0.062326
函数计算时间 = 6.157
估计的最佳可行点(根据模型):
Activations Standardize Lambda LayerSizes
___________ ___________ __________ _________________
sigmoid true 3.6739e-06 211 51 5
估计的目标函数值 = 0.062326
估计的函数计算时间 = 6.2702
准确率为:
0.8966