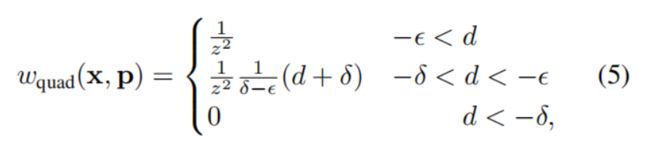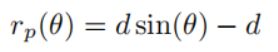voxblox论文翻译以及部分代码解析
【地图构建】voxblox地图:用于MAV路径规划的增量式3D欧几里得符号距离场(ESDFs) - 知乎 (zhihu.com)
应用于三维重建的TSDF(一)原理与代码解析 - 简书 (jianshu.com)
应用于三维重建的TSDF(二)voxblox 代码解析 - 古月居 (guyuehome.com)
应用于三维重建的TSDF(三)voxblox代码解析 - 古月居 (guyuehome.com)
(24条消息) 机器人建图算法2.1从栅格占据地图到ESDF地图_RuiH.AI的博客-CSDN博客
Voxblox 论文笔记 – 风林轩 (krmzyc.com)
Voxblox
主要贡献:
1)第一个能在地图动态增长的情况下,从TSDFs中增量式的构建ESDFs的方法
2)为了最大化在大体素(large voxel sizes)的情况的TSDFs的重建速度和表面准确度,分析了不同的构建TSDFs的方法。
3)提供了定量的和实验上的关于ESDFs误差的分析,并且提出了安全的克服这些误差的补丁
4)通过在无人机上使用这些地图以及在线再规划来验证整个系统。
本程序的实现用到了哈希表:
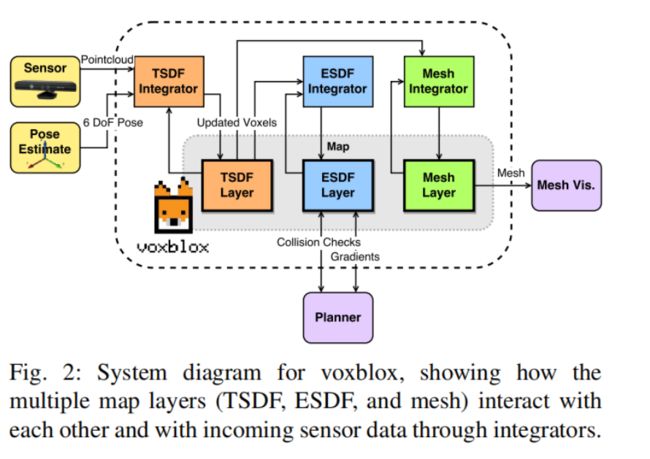
为了使得这个地图更适合用于探索和建图应用,我们使用一个利用了体素哈希方法的有动态大小的地图。每一种体素(voxel)(不论是TSDF还是ESDF)都有属于它的层(layer),并且每个层都有独立的块(block),其中这些块是通过它们在地图中的位置来建立索引的。块位置和它们在内存中的位置之间的映射是储存在哈希表中的,这个允许o(1)的插入和查找操作。这样就使得数据结构能够更加灵活的用来建立地图,并且可以获得比八叉树地图更快的查询速度。
这是整个地图的流程,ESDFs用来给无人机规划路径,TSDFs用来生成网格,以便给人类观看
TSDF构建过程:
A:加权(weighting)
Kinectfusion 讨论说使用基于 θ \theta θ 的权重, θ \theta θ 是从原点出发的光线到表面法线之间的角度,然而却说常量权重1已经足够在毫米级的体素上得到一个好结果。
我们建议使用一个复杂的权重与上面显示的权重进行对比,bylow等人比较了在等表面边界之后进行权重下降的结果,然后发现一个线性的权重下降通常会得到更好的结果。
控制整合过程的广泛方程是基于现有距离、体素的权重,D 和W,以及新的更新值是来自于在传感器中的特定点的观测,d和w,其中d是从表面边界过来的距离。考虑x是现有体素的中心位置,p是不断来到的3D数据点的位置,s是传感器原点,并且 x , p , s ∈ R 3 x,p,s \in R^3 x,p,s∈R3 ,在x处的更新过的D距离和W由下式得到:
nguyen等人根据经验确定了一个RGBD模型,发现单一射线测量值的 σ \sigma σ的变换主要与 z 2 z^2 z2 有关系,我们把一个近似简化后的RGBD模型与behind-surface下降模型结合起来,如下
B:合并
当我们专注于使用更大的体素大小来加速计算的时候,一个重要的需要考虑的就是如何使得新的扫描数据被整合到现有的体素网格中(voxel grid),对于大的体素(大约几十厘米)来自同一次扫描产生的数千个射线也许会映射到同一个voxel,我们利用这一点通过设计一个对每一个end voxel只执行一次光线投射的策略来显著提高速度。
这两有两种主要的可以把传感器数据整合到TSDF里面的方法:【光线投射】,【投影映射】
【光线投射】:光线投射从相机光心出发,到观测到的每一个点的中心,更新从中心到截断距离 δ \delta δ之间的所有体素。
【投影映射】:把在可视区域内的体素投影到深度图里面,同时计算它的距离:在深度图中的值与体素中心的距离,这样做非常的快,但是在大的体素上会导致很严重的混叠效应
我们提出的新方法**【分组光线投射】(grouped raycasting):显著的加速了光线投射速度,但是又不会损失太多的准确度。**对于在传感器数据中的每一个点,我们把它的位置给投影到体素里面,然后把它和所有的被映射到同一个体素的点分成一组,然后我们计算在体素内的所有点和颜色的加权平均值,然后只做一次光线投射在这个平均的位置上。因为所有的观测值都被考虑到了,并且他们的权重和距离是像往常一样被组合,这样就得到了一个非常相似的重建效果但是却比普通的光线投射方法要快了20倍。
(一次性投影多个点到一个大的体素当中,这样就不需要每个点都更新路过的体素了,只需要将体素内加权平均出来一个位置,更新传感器到这个点的位置之间的体素即可)
从TSDF构建ESDF(不清晰)
How Does ESDF Generation Work? — voxblox documentation
A.构建
我们的方法基于Lau等人的工作,他提出了一种从占用地图[4]动态更新 E S D F s ESDF_s ESDFs的快速算法。我们扩展了他们的方法,以利用 T S D F s TSDF_s TSDFs作为输入数据,并允许ESDF地图动态地改变大小。完整的方法如算法1所示,其中 v T v_T vT表示原始TSDF地图中的一个体素, v E v_E vEESDF地图中的共定位体素。
我们所做的一个关键改进是使用存储在TSDF映射中的距离,而不是计算到最近被占用体素的距离。在最初的实现中,每个体素都有一个被占用或空闲的状态,算法不能改变。相反,我们将这个概念替换为一个固定带和表面:**ESDF体素,它从它们位于同一位置的TSDF体素中获取它们的值,并且可能不会被修改。**固定带的大小由TSDF体素定义,其距离满足 ∣ v T . d ∣ < γ |v_T.d | < γ ∣vT.d∣<γ,,其中 γ \gamma γ是带的半径,在V-B节中进一步分析。
一般算法基于波阵面——波从一个起始体素传播到它的邻居(使用26连通性),更新它们的距离,并将更新的体素放入波前队列中,进一步传播到它们的邻居。我们使用两个波阵面:上升波阵面和下降波阵面。当一个体素与TSDF之间的新距离值大于存储在ESDF体素中的前一个值时,该体素将被添加到上升队列。这意味着体素及其所有子元素都需要失效。波阵面一直传播,直到没有体素留下已失效的父体素为止。
不像Lau et al.[4],他们分散,我们首先提高所有体素,然后降低所有体素,以减少记录。此外,当它们将未知体素视为已占用时,我们不会更新未知体素。对于每个体素,我们存储指向父元素的方向,而不是父元素的完整索引。对于准欧几里得距离(在算法中显示),这个父方向是指向相邻体素的,而对于欧几里得距离,它包含到父的完整距离。关于欧几里得距离与准欧几里得距离的完整讨论将在下一节中提供。
最后,由于新的体素可以在任何时候进入地图,每个ESDF体素都会跟踪它是否已经被观察到。然后,我们在算法1的第20行中使用它来为新体素做簿记的关键部分:将它们的所有邻居添加到较低的队列中,这样新的体素将被更新为有效值。
我们的方法合并了一个桶形优先级队列来跟踪哪些体素需要更新,优先级为 ∣ d ∣ |d| ∣d∣。在结果中,我们比较了两种不同的变体:FIFO队列和优先级队列(其中具有最小绝对距离的体素首先更新)。
B.ESDF的误差来源S
在使用地图进行规划时,必须了解该方法对最终距离计算误差的影响。在本节中,我们的目标是量化我们的近似的效果,并推荐一个安全边缘,通过它来增加用于规划的包围框。
我们考虑了最终ESDF误差的两个关键因素:第一,TSDF投影距离计算,第二,距离计算中的准欧几里得近似。
投影距离(沿相机射线到表面的距离)将总是匹配或高估实际到最近曲面的欧几里得距离。因此,为了使用与TSDF的投影距离,我们需要量化这将引入的误差。误差取决于d,体素的测量距离,和θ,相机光线和物体表面之间的入射角。我们假设局部平面物体。投影误差残差 r p ( θ ) r_p(\theta ) rp(θ)可表示为:
为了分析的目的,我们假设入射角θ可以在π/20和π/2之间,并且在这个范围内均匀分布。π/20的下界来自于观察到,由于相机的物理尺寸,相机光线不能平行于曲面边界,相机也不能无限小地靠近曲面。π/20对应的MAV距离表面至少1米,传感器射线的最大长度为5米。假设f(O)是π/20和π/2之间的均匀分布,因为这是对称的,那么单个体素观测的预期误差将是:
注意d有截断距离$\delta $的上界。
然而,这并不考虑对同一体素的多次观察,这将降低这个误差。为了量化这一点,我们执行了合并同一体素的多个独立测量的蒙特卡洛模拟,如图3所示。结果表明,即使只有3个观测值,误差的上界为0.5δ, p = 0.95,并且随着观测数的增加,该概率下的误差减小到0.25$\delta $以下。
这取决于固定带的大小如何决定这是对这个错误的很大补偿。如果只使用表面边界的单个体素,那么将安全距离增加一个体素的一半是安全的。
考虑的第二个误差来源是ESDF计算中的准欧几里得距离假设。拟欧氏距离沿网格中的水平线、垂直线和对角线测量,当曲面法线与曲面到体素的射线夹角为45°的倍数时无误差,最大误差为φ = 22.5°[20]。如果φ在0和π/4之间均匀分布,则此误差的残差r(Φ),其最大值和期望值为:

由于本例中的d在最大ESDF计算距离中只有一个上界,我们建议将机器人的包围框膨胀8.25%。部分VI-B对这种假设对ESDF计算中的总体误差有什么影响有经验结果,并表明在实践中它足够小,足以证明全欧几里得距离和准欧几里得距离之间的加速。
代码阅读:
TSDF Integrator
void MergedTsdfIntegrator::integratePointCloud()
void FastTsdfIntegrator::integratePointCloud()
void SimpleTsdfIntegrator::integratePointCloud()
分别对应着我们前面简要提到的voxblox提供的三种tsdf的积分方法。如果我们一开始在launch文件里选择的是merged方法,那么就会进入第一个点云积分方法。 在第一讲里面我们也提到过tsdf的获取方法分为两种。这儿的"三"和"两"不能搞混。
两种获取tsdf的方法讲的是如何把传感器的信息融合到tsdf里面去。第一种方法我们在第一讲已经讲到过,是通过把所有voxel投影到当前相机的坐标系下,比较图像3d点的z和深度voxel的z的差距获得tsdf。而第二种方法,是voxblox采用的方法,它会从相机的中心(optical center)投射一条射线(cast a ray)到所有图像2d点投影的3d点,从相机中心到这些点之后的(距离相机更远的),距离小于截断距离 δ \delta δ的voxel都会被更新。
针对第二种融合方法,voxblox再提出了两种加速的方法即。其一就是Fast其二就是Merged。普通方法对每一个图像点都投影射线,计算太慢,Merged方法先计算哪些3d点投影到了相同的voxel里,**然后取这些点的坐标平均数,视为一个点,**只从那个平均点投影射线,利用上面的方法二更新。可以想象,如果voxel_size设置得大,会更容易有更多点投影到一个voxel里被平均,那么它的速度提升会更明显。
进入bundleRays()函数
while (index_getter->getNextIndex(&point_idx)) { ... //获得世界坐标系下的点
const Point point_G = T_G_C * point_C;
//getGridIndexFromPoint会计算世界坐标系下的点在哪个voxel里,其实原理很简单,假设第voxel_size=0.06,那么从原点开始的第一个voxel就包含了0.06X0.06X0.06这么大的空间。
//如果我们有一个点坐标是(0.01,0.01,0.01),那么我们可以肯定它在这个voxel之内。
//数学表达为
//voxel_id_x = p.x / voxel_size = p.x * voxel_size_inv
//voxel_id_y = p.y / voxel_size = p.y * voxel_size_inv
//voxel_id_z = p.z / voxel_size = p.z * voxel_size_inv
GlobalIndex voxel_index = getGridIndexFromPoint<GlobalIndex>(point_G, voxel_size_inv_);
//有些不valid的点是需要清除的(距离相机太近或太远之类,见IsValid函数)除此之外,那些投影到一个voxel_index下的不同poin_idx都会被push到voxel_map里。
if (is_clearing) { (*clear_map)[voxel_index].push_back(point_idx); }
else { (*voxel_map)[voxel_index].push_back(point_idx); } }
回到MergedTsdfIntegrator::integratePointCloud函数
...bundleRays(T_G_C, points_C, freespace_points, index_getter.get(), &voxel_map,&clear_map);
//在我们确定了哪些poins属于相同的voxel_idx之后,就可以把那些points作为同一个点去更新voxel的tsdf了。
integrateRays(T_G_C, points_C, colors, config_.enable_anti_grazing, false,voxel_map, clear_map);
进入integrateRays函数
//多线程并行调用integrateVoxels函数
integration_threads.emplace_back(&MergedTsdfIntegrator::integrateVoxels, this, T_G_C, points_C, colors,enable_anti_grazing, clearing_ray, voxel_map, clear_map, i);
进入到integrateVoxels函数
//这个迭代器it会挨个迭代每个voxel_map里的元素,记住我们的voxel_map[i]本身也是一个vector,它储存了属于同一个voxel的点
LongIndexHashMapType<AlignedVector<size_t>>::type::const_iterator it;...
//*it代表属于同一个voxel的点合成的向量,integrateVoxel会把*it里的点的位置/颜色求平均。
integrateVoxel(T_G_C, points_C, colors, enable_anti_grazing, clearing_ray, *it, voxel_map)...it++
进入integrateVoxel函数
//求得属于一个voxel内的点的平均点和颜色
for (const size_t pt_idx : kv.second) {...
merged_point_C = (merged_point_C * merged_weight + point_C * point_weight) / (merged_weight + point_weight);
merged_color = Color::blendTwoColors(merged_color, merged_weight, color, point_weight);
merged_weight += point_weight;... }...
//利用平均点投影射线
RayCaster ray_caster(origin, merged_point_G, clearing_ray,config_.voxel_carving_enabled, config_.max_ray_length_m, voxel_size_inv_, config_.default_truncation_distance);
进入位于integrator_utils.cc的RayCaster构造函数
//计算单位射线的长度,就是简单的求点到原点的差值,求得他们的norm(均方值)再每一个维度除以norm归一化。
const Ray unit_ray = (point_G - origin).normalized();...
//射线的开始点为原点(voxel_carving_enabled==true),终止点为平均点后unit_ray * truncation_distance的位置。
//正如我们在前面讲算法时提到的,要计算从原点到当前被观察到的点后距离为truncation_distance的所有voxel
ray_end = point_G + unit_ray * truncation_distance;
ray_start = voxel_carving_enabled? origin:(point_G - unit_ray * truncation_distance);...//cast_from_origin == false
setupRayCaster(end_scaled, start_scaled);
进入setupRayCaster函数
//首先获取射线开始位置和结束位置对应的voxel的三个方向的index的坐标以及差值
curr_index_ = getGridIndexFromPoint<GlobalIndex>(start_scaled);
const GlobalIndex end_index = getGridIndexFromPoint<GlobalIndex>(end_scaled);
const GlobalIndex diff_index = end_index - curr_index_;
//ray_step_signs_很有意思,这个值的每个维度(x,y,z)只可能为3个值, 1,-1或者0. 我们会在后面看到它的用处
ray_step_signs_ = AnyIndex(signum(ray_scaled.x()), signum(ray_scaled.y()),signum(ray_scaled.z()));//后面处理一些边界问题,暂时不讲...
一直返回到tsdf_integrator.cc的MergedTsdfIntegrator::integrateVoxel
...//上面RayCast构造函数设置了射线的一些性质,比如它的长度等
RayCaster ray_caster(origin, merged_point_G, clearing_ray,config_.voxel_carving_enabled, config_.max_ray_length_m, voxel_size_inv_, config_.default_truncation_distance);
//进入while循环,循环里会遍历射线上从原点开始到平均点之后的`unit_ray * truncation_distance`距离内的所有voxelGlobalIndex global_voxel_idx;
while (ray_caster.nextRayIndex(&global_voxel_idx)){}
进入nextRayIndex函数
if (current_step_++ > ray_length_in_steps_)
{ return false; }
//最关键是下面这行,我们之前说过ray_step_signs_只为0,-1或者1。所以curr_index其实就会加减1或者不动,那其实每调用一次这个函数,voxel三个维度的坐标就会加减1或者不动。一直到遍历的step>ray_length_in_steps_为止。这就是遍历射线上所有体素的方法...
curr_index_[t_min_idx] += ray_step_signs_[t_min_idx];...
回到MergedTsdfIntegrator::integrateVoxel的while循环
GlobalIndex global_voxel_idx;
while (ray_caster.nextRayIndex(&global_voxel_idx)){...Block<TsdfVoxel>::Ptr block = nullptr;
BlockIndex block_idx;
//文章最开始有介绍,我们是有8X8X8的voxel组成一个block。只有在block里的voxel才会被分配空间真正储存起来(有tsdf值,rgb值等)。下面这行函数就是检测该voxel是否已经属于某个block还是并不属于任何一个block,如果不,则新建一个block分配空间。返回在这个block里的对应index的voxel
TsdfVoxel* voxel = allocateStorageAndGetVoxelPtr(global_voxel_idx,&block,&block_idx);
//终于,做了那么多准备,更新tsdf
updateTsdfVoxel(origin, merged_point_G, global_voxel_idx, merged_color, merged_weight, voxel);...}
进入updateTsdfVoxel函数(逐帧)
//计算voxel中心的x,y,z坐标
const Point voxel_center = getCenterPointFromGridIndex(global_voxel_idx, voxel_size_);
//计算voxel中心到原点的直线距离,计算观察到的平均点到原点的直线距离。原点到voxel的射线和平均点到原点的射线一般不会完全共线,因此在这个函数里会voxel的射线投影到平均点的射线上,再做个减法获得sdf。
//voxblox论文公式1
const float sdf = computeDistance(origin, point_G, voxel_center);
//更新voxel的权重,在线面这行代码之前,其实有一定的计算过程。我们在第一讲里有说到每一帧的每个voxel的权重更新都是简单的加1.voxblox提出了根据截断距离的大小来动态改变权重的方法,可参见论文公式
//2. updated_weight不再只是1,不过最后的更新的方法不变,加到原本的tsdf_voxel->weight上去...
const float new_weight = tsdf_voxel->weight + updated_weight;
//论文公式3,更新sdf
const float new_sdf = (sdf * updated_weight + tsdf_voxel->distance * tsdf_voxel->weight) / new_weight;
//接下来更新rgb颜色(如果有的话),并对sdf进行截断得到tsdf
// color blending is expensive only do it close to the surface
if (std::abs(sdf) < config_.default_truncation_distance) { tsdf_voxel->color = Color::blendTwoColors( tsdf_voxel->color, tsdf_voxel->weight, color, updated_weight); }
//截断
tsdf_voxel->distance = (new_sdf > 0.0) ? std::min(config_.default_truncation_distance, new_sdf) : std::max(-config_.default_truncation_distance, new_sdf);
//论文公式4. tsdf_voxel->weight = std::min(config_.max_weight, new_weight);
Mesh Integrator
在TsdfServer::TsdfServer构造函数里设置好mesh更新频率之后,updateMeshEvent函数会按照这个频率运行。
if (update_mesh_every_n_sec > 0.0) {
update_mesh_timer_ = nh_private_.createTimer(ros::Duration(update_mesh_every_n_sec),
&TsdfServer::updateMeshEvent, this);
}
double publish_map_every_n_sec = 1.0;
nh_private_.param("publish_map_every_n_sec", publish_map_every_n_sec, publish_map_every_n_sec);
进入updateMeshEvent
void TsdfServer::updateMeshEvent(const ros::TimerEvent& /*event*/) {
updateMesh();
}
进入updateMesh
...
constexpr bool only_mesh_updated_blocks = true;
constexpr bool clear_updated_flag = true;
mesh_integrator_->generateMesh(only_mesh_updated_blocks, clear_updated_flag);
进入mesh_integrator.h的generateMesh函数
//返回所有voxel有更新的block的index
if (only_mesh_updated_blocks) {
sdf_layer_const_->getAllUpdatedBlocks(Update::kMesh, &all_tsdf_blocks);
}
//mesh和block有对应关系,如果有新建的block而没有对应的mesh,则为mesh分配新的空间。
// Allocate all the mesh memory
for (const BlockIndex& block_index : all_tsdf_blocks) {
mesh_layer_->allocateMeshPtrByIndex(block_index);
}
...
//多线程运行generateMeshBlocksFunction函数
std::list<std::thread> integration_threads;
for (size_t i = 0; i < config_.integrator_threads; ++i) {
integration_threads.emplace_back(
&MeshIntegrator::generateMeshBlocksFunction, this, all_tsdf_blocks,
clear_updated_flag, index_getter.get());
}
进入generateMeshBlocksFunction函数
//每个线程要遍历`all_tsdf_blocks`里的部分block
while (index_getter->getNextIndex(&list_idx)){
const BlockIndex& block_idx = all_tsdf_blocks[list_idx];
updateMeshForBlock(block_idx);
}
进入updateMeshForBlock函数,针对某个的block_id更新mesh
//根据已建立的mesh和block的对应关系,找到各自的指针
Mesh::Ptr mesh = mesh_layer_->getMeshPtrByIndex(block_index);
mesh->clear();
typename Block<VoxelType>::ConstPtr block =
sdf_layer_const_->getBlockPtrByIndex(block_index);
extractBlockMesh(block, mesh);
进入extractBlockMesh
//对block里的每一个voxel进行操作。
IndexElement vps = block->voxels_per_side();
VertexIndex next_mesh_index = 0;
VoxelIndex voxel_index;
for (voxel_index.x() = 0; voxel_index.x() < vps - 1; ++voxel_index.x()) {
for (voxel_index.y() = 0; voxel_index.y() < vps - 1; ++voxel_index.y()) {
for (voxel_index.z() = 0; voxel_index.z() < vps - 1; ++voxel_index.z()) {
//获取block里每一个voxel的x,y,z坐标
Point coords = block->computeCoordinatesFromVoxelIndex(voxel_index);
extractMeshInsideBlock(*block, voxel_index, coords, &next_mesh_index,mesh.get());
}
}
}
进入extractMeshInsideBlock函数
//这里开始涉及到我们上一讲的marching cubes了。设立了一个立方体8个顶点,每个顶点有x,y,z坐标值,所以有//根据8个顶点的sdf,获得一个8位的int常量index,该量上的每一位代表tsdf的正负,如果为正则那一位为1,否则为0
const int index = calculateVertexConfiguration(vertex_sdf);
...
//对12条边进行插值。有符号变化的两个相连的顶点之间就会被插值
Eigen::Matrix<FloatingPoint, 3, 12> edge_vertex_coordinates;
interpolateEdgeVertices(vertex_coords, vertex_sdf,
&edge_vertex_coordinates);
//根据每个顶点的tsdf的正负获得的index,传入kTriangleTable里,这样我们就知道需要在哪些边上插值。
//打开kTriangleTable你会看到他是256*16的变量。正如我们上一讲讲到的256个cube里插值的可能性
const int* table_row = kTriangleTable[index];
接着浏览meshCube里的代码
const int* table_row = kTriangleTable[index];
//while循环结束的条件就是遇到table_row[table_col] == -1
int table_col = 0;
while (table_row[table_col] != -1) {
//前面interpolateEdgeVertices已经计算好了哪些边有插值点哪些边没有.
//这里我们只需要根据table_row[table_col]选出是哪几条边插值了顶点. push到mesh里。我们就可以根据那几个点建立一个tsdf为0的面了。
mesh->vertices.emplace_back(edge_vertex_coordinates.col(table_row[table_col + 2]));
mesh->vertices.emplace_back(edge_vertex_coordinates.col(table_row[table_col + 1]));
mesh->vertices.emplace_back(edge_vertex_coordinates.col(table_row[table_col]));
mesh->indices.push_back(*next_index);
mesh->indices.push_back((*next_index) + 1);
mesh->indices.push_back((*next_index) + 2);
const Point& p0 = mesh->vertices[*next_index];
const Point& p1 = mesh->vertices[*next_index + 1];
const Point& p2 = mesh->vertices[*next_index + 2];
...
可以退回到updateMesh函数。
//完成这一行后,我们上面的marching_cube就建立完毕
mesh_integrator_->generateMesh(only_mesh_updated_blocks, clear_updated_flag);
...
voxblox_msgs::Mesh mesh_msg;
//把我们得到的marching cube插值得到的表面转化为ros message,发布,可视化
generateVoxbloxMeshMsg(mesh_layer_, color_mode_, &mesh_msg);
mesh_msg.header.frame_id = world_frame_;
mesh_pub_.publish(mesh_msg);
复制
在voxblox_mesh_visual.cc的setMessage函数里,定义了接收到的消息要如何可视化。其中比较重要的部分
// connect mesh把所有mesh连起来
voxblox::Mesh connected_mesh;
voxblox::createConnectedMesh(mesh, &connected_mesh);
// create ogre object 。rviz会根据ogre object的设置来决定如何可视化
Ogre::ManualObject* ogre_object;
...
//定义ogre要绘制的是一系列三角形面`OT_TRIANGLE_LIST`. `BaseWhiteNoLighting`为三角形可选择的表面打光的方式
//可以选择的方式请自行去ogre官网查看
ogre_object->begin("BaseWhiteNoLighting", Ogre::RenderOperation::OT_TRIANGLE_LIST);
//在选择了要绘制以三角形为基础的面片之后,就进入for循环,往ogre_object里push数据
for (size_t i = 0; i < connected_mesh.vertices.size(); ++i) {
// note calling position changes what vertex the color and normal calls
// point to
// 由于设置的是绘制三角形,所以这个循环每走三次,push进去三个点,ogre就会自动连接这三个点
ogre_object->position(connected_mesh.vertices[i].x(),
connected_mesh.vertices[i].y(),
connected_mesh.vertices[i].z());
...
//之后还需要push每个点的颜色,normal等,ogre会自动插值来决定三角面片的颜色