Diffusion Model
文章目录
- Diffusion Model如何运作(DDPM)?
-
- Reversed Process
- 监督信号
- 添加文本
- 关键算法
- 目前的Diffusion Model的结构
-
- 目前DM的基本结构
- Text Encoder
-
- FID
- CLIP Score
- Decoder
- Generation Model
- 一些疑问
- Diffusion Model背后的数学原理
-
- 关键算法解析
-
- 训练Noise Predictor
- 产生图的过程
- 影像生成模型本质上的共同目标
-
- 如何保证目标分布和真实分布一致呢?
- 最大化似然函数
-
- VAE是如何计算的?
- DDPM是如何计算的?
- 如何最大化DDPM的下界?
- 如何最小化第三部分中的KL散度?
-
- 怎么计算 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)(为什么生成训练数据是一步到位的)?
- Stable Diffusion
-
- Motivation
- Method
Diffusion Model如何运作(DDPM)?
Reversed Process
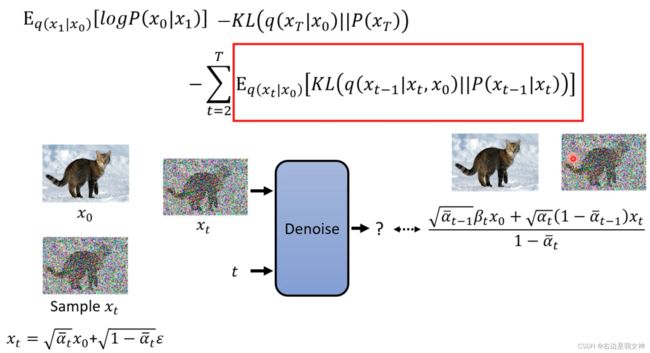
第一步是生成一个和目标图片一模一样的噪声图像. 之后, 不断通过Denoise的模块(编号逐渐变小, 同一个Denoise model重复)去噪, 以得到图像.
上述过程称为Reversed Process, 类似雕塑的过程.
为了重复使用Denoise Model解决不同程度的去噪, 额外输入一些数据(严重程度,步骤代号).
监督信号
那么如何训练Noise Predictor? 即如何创建监督信号?
对原图不断加噪声得到噪声图像.
添加文本
关键算法
目前的Diffusion Model的结构
目前DM的基本结构
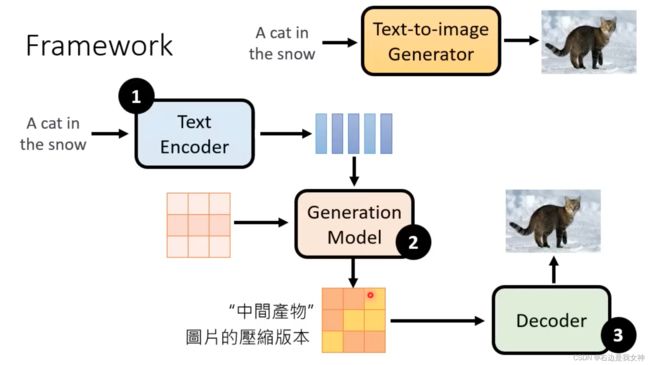
中间产物是小图或者Latent Representation.
目前常用的有DALL-E, Stable Diffusion, Imagen.
Text Encoder
对于文本编码器, 规模越大, 效果越好. Diffusion Model的规模对生成图像效果的影响不大.
FID
生成 生成图像和真实图像 的两组表征, 假设它们都符合高斯分布, 计算它们之间的Frechet Distance.
CLIP Score
计算 输入文本和生成图像的相似度.
Decoder
Decoder的训练不需要文本资料.
训练一个AutoEncoder.
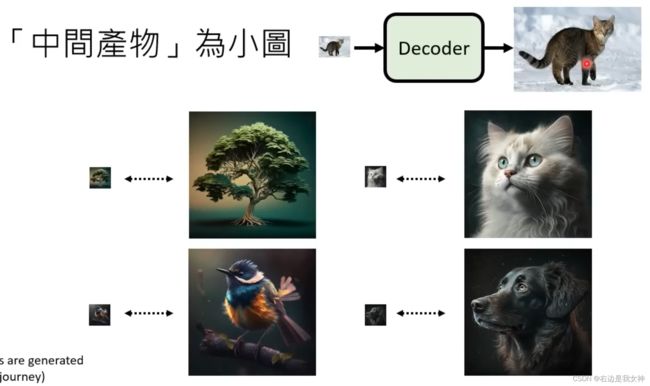
做下采样, 得到训练数据.
DALL-E, Stable Diffusion是前者, Imagen是后者.
Generation Model
原本的DDPM中, Generation Model生成的是一张图像, 所以可以对图像加噪声制作训练数据. 但此时其生成的是中间产物, 那么又该作何处理?
自然而然的想法是把噪声加载中间产物上. 中间产物通过下采样或者Encoder得到.
之后和一般的Diffusion Model是完全一样的.
推理过程为:
Midjourney的生成过程是由模糊到清晰, 这是因为每一个Denoise的输出都被Decoder解码呈现.
一些疑问
- 为什么之前的Diffusion Model没有解码器?
- 之前的文本是以何种形式输入给Noise Predictor的?
- 去噪的Mask是如何得到的?
Diffusion Model背后的数学原理
关键算法解析
训练Noise Predictor
t越大, a ˉ t \bar{a}_t aˉt越小, 即增加的噪声越大, 这些数据是预定义的.
根据有噪声的图预测混入的噪声是什么样(这边噪声符号写错了).
实际上是直接混入噪声, 噪声大小有区分, 并不是一点一点加入噪声的.
关键问题:为什么是一步到位生成训练数据而不是逐步的?
产生图的过程
关键问题: 为什么还要在降噪的图像上增加噪声?
影像生成模型本质上的共同目标
原始分布通过生成模型得到目标分布, 目标分布应该与真实分布类似.
目前的生成模型往往要求文字的影响:
加上文字的condition本质上没有改变什么, 所以后续的推导不包括文本.
如何保证目标分布和真实分布一致呢?
- 从真实分布采样一些样本;
- 计算这些样本在目标分布中的概率;
- 训练目标是找到一组参数, 让这一概率大.
最大化似然等价于最小化KL散度.
最大化似然函数
VAE是如何计算的?
VAE实际上算出的是 P ( x ) P(x) P(x)的下界.
DDPM是如何计算的?
对每一个变量做积分.
q q q的分布在VAE中时Encoder的输出的分布, 在Diffusion Model中是Forward Process, 即由原图生成噪声图像的分布.
如何最大化DDPM的下界?
通过上述的计算, 得到我们真正要优化的目标.
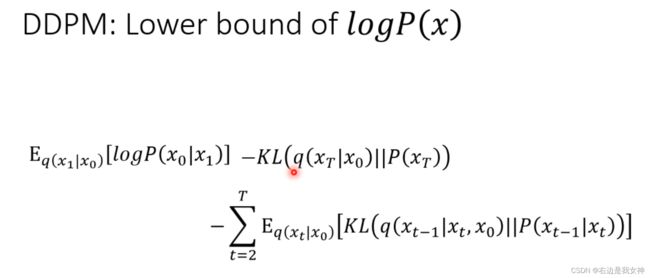
中间项和模型的参数无关, 可以直接无视. 因此, 我们只考虑第一项和第三项.
如何最小化第三部分中的KL散度?
计算前者分布的均值和方差:
仍然是一个高斯分布, 均值和方差如上.
P P P的均值是可调整的, 方差是不可以的. 所以为了让这两个分布接近, 调整两个分布的均值即可.
我们对目标进行化简:
最大化似然函数 -> 最大化下界函数 - > 最小化KL散度 -> 最小化范数(每一时间步的输出和分布q的均值接近) -> 最小化范数(预测噪声和真实噪声接近)
在文本生成, 语言合成都需要加入一点noise才会得到比较好的效果.
怎么计算 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)(为什么生成训练数据是一步到位的)?
我们已经知道输出的计算公式, 其中噪声是通过denoise模块得到的, 那么我们如何训练denoise模块呢?
公式中 α \alpha α的产生也与该分布有关.
q ( x t ∣ x 0 ) q(x_t|x_0) q(xt∣x0)看似是渐进的过程, 实际上是可以直接算出来的.
上图中的 β t \beta_t βt是预定义的参数. 控制不同时间步的噪声和图像的加权. t t t的值越大, 噪声的权重会越大.
采样两次得到的分布等同于采样一次, 这是根据独立的正态分布的可加性.
此时, x 0 x_0 x0的系数已经确定, 为了控制噪声和输入图像的权重, 因此才得到如此的噪声系数.
如此一来, 采样一次即可.
Stable Diffusion
Motivation
扩散过程在像素空间上进行, 这会带来极大地计算开销. 本文的目的是将扩散过程带到隐空间进行, 在降低计算开销的同时维护模型的性能.
Method
Diffusion Models: L D M = E x , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( x t , t ) ∥ 2 2 ] L_{DM}=\mathbb{E}_{x,\epsilon\sim N(0,1),t}[\|\epsilon-\epsilon_\theta(x_t, t)\|^2_2] LDM=Ex,ϵ∼N(0,1),t[∥ϵ−ϵθ(xt,t)∥22]
Latent Diffusion Model: L L D M = E ε ( x ) , ϵ ∼ N ( 0 , 1 ) , t [ ∥ ϵ − ϵ θ ( z t , t ) ∥ 2 2 ] L_{LDM}=\mathbb{E}_{\varepsilon(x),\epsilon\sim N(0,1),t}[\|\epsilon-\epsilon_\theta(z_t, t)\|^2_2] LLDM=Eε(x),ϵ∼N(0,1),t[∥ϵ−ϵθ(zt,t)∥22]
