【C进阶】深度剖析数据在内存中的存储

目录

一、数据类型的介绍

1.类型的意义：

2.类型的基本分类

二、整形在内存中的存储

1.原码 反码 补码

2.大小端介绍

3.练习

三、浮点型在内存中的存储

1.一个例子

  2.浮点数存储规则

---

一、数据类型的介绍

前面我们已经学习了基本的内置类型以及他们所占存储空间的大小：

char          //字符数据类型

short         //短整型

int             //整形

long          //长整形

long long   //更长的整形

float           //单精度浮点型

double      //双精度浮点型

1.类型的意义：

1.使用这个类型开辟内存空间的大小（大小决定了使用的范围）

2.决定了如何看待内存空间的视角：

int 和float类型都是4个字节，但是一个是整形，一个是浮点型，看待内存空间的视角不一样

2.类型的基本分类

(1)整形家族：

char：

        unsigned char

        signed  char

short :

       unsigned short  [int]     //短整型，这个int整形可以省略

        signed  short   [int]

int :

      unsigned int

        signed  int

long :

       unsigned long [int]

        signed  long [int]

【温馨提示】：char类型也是整形家族的原因：

字符在内存中存储的是字符的ACSII码值（0-127），ASCII码值是整形，所以字符类型归类到整形家）族 

signed -有符号的：当第一位代表符号位的时候，就是有符号的

unsigned -无符号的：当每一位都是数值位，有效位的时候就是无符号的

【注意】：

当我们没有写signed和unsigned时，int，short和long类型默认就是signed有符号的

eg：当我们写出int a的默认的其实就是signed int类型

but ：C语言并没有规定char是否是signed char（这个取决于编译器，大部分是signed char）

---

(2)浮点数家族：都可以表示小数

 float     //精度小一些，单精度

double   //精度大一些，双精度

---

(3)构造类型（自定义类型）

>数组类型

>结构体类型 struct

>枚举类型 enum

>联合类型 union

---

(4)指针类型

int *pi

char *pc

float *pf

void * pv  (无具体类型的指针）

---

(5) 空类型

void 表示空类型（无类型）

通常应用于函数的返回类型，函数的参数，指针类型

eg：int main（void）就表示main函数不需要参数

但是实际上main函数是有三个参数的int main(int argc,char *argv[  ],char *envp[  ]),这三个参数需要用的时候才需要写，不需要括号直接写void即可

二、整形在内存中的存储

计算机能够处理的是二进制数据，整形和浮点型在内存中也都是以二进制的形式进行存储的

1.原码 反码 补码

整形的二进制表示有三种：原码，反码，补码

正的整数：原码，反码，补码相同

负的整数：原码，反码，补码要进行计算

整数在内存中存储的是补码的二进制序列

eg：

int a = -10;//int类型占4个字节-32bit位
    10000000 00000000 00000000 00001010  原码
    11111111 11111111 11111111 11110101  反码
    1 1111111 11111111 11111111 11110110  补码（最高一位表示符号位，其他31位表示数值位）

    unsigned int b = -10;
    1 1111111 11111111 11111111 11110110  补码（32位全都表示数值位）

---

对于整形来说，数据存放内存中其实存放的是补码

为什么呢？

使用补码，可以将符号位和数值域统一处理；同时，加减法也可以统一处理（cpu只有加法器），此外，补码和原码相互转换，其运算过程是相同的，不需要额外的硬件电路

eg：

    1-1
    电脑转化为1+(-1)
    00000000 00000000 00000000 00000001  1的原反补码
    10000000 00000000 00000000 00000001  -1的原码
    11111111 11111111 11111111 11111110  -1的补码
    11111111 11111111 11111111 11111111  -1的补码
    如果就是简单的原码相加得到的就是-2（还会犹豫要不要加符号位）
    但是如果是补码相加得到的就是正确的结果，每个位上不断进1，最后最前面多出来一位为1直接舍弃，其他位都为0

2.大小端介绍

int a=0x11223344（根据数据的存储44位于低字节处，11位于高字节处）

大端字节序存储：

把一个数据的低位字节处的数据存放在内存的高地址处，高位字节处的数据存放在内存的低地址处

小端字节序存储：

把一个数据的低位字节处的数据存放在内存的低地址处，高位字节处的数据存放在内存的高地址处

【注意】：数据存放的时候是以字节为单位存储讨论顺序的，所以叫做大小端字节序存储

char类型不需要考虑大小端，char类型就占一个字节，没有顺序可言

---

为什么存在大小端字节序存储呢？

这是因为在计算机系统中，我们是以字节为单位的，每个地址单元都对应着一个字节，一个字节为8 bit。但是在C语言中除了8 bit的char之外，还有16 bit的short型，32 bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式

---

百度笔试题:

请简述大端字节序和小端字节序的概念，设计一个程序来判断当前机器的字节序

思路：

给一个int类型的变量a：让其为1（这样十六进制简单0x 00 00 00 01），然后再通过char*一次访问一个字节，打印出来看是00还是01，从而判断大小端

代码实现：

#include
int main()
{
	int a = 1;
	char* p = (char*)&a;   //要将&a（int *）强制转化为char *
	if (*p == 1)
		printf("小端\n");
	else
		printf("大端\n");
	return 0;
}

【自定义函数进行判断】：

#include
int check_sys()
{
	int a = 1;
	return *(char*)&a;
}
int main()
{
	if(check_sys()==1)
		printf("小端\n");
	else
		printf("大端\n");
	return 0;
}

---

3.练习

<1>下面程序输出什么？

#include 
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;

printf("a=%d,b=%d,c=%d",a,b,c);

return 0;
}

答案：

-1 -1 255

解释：

首先-1是整数，原码：10000000 00000000 00000000 00000001

                         反码：111111111 111111111 111111111 111111110

                         补码：111111111 111111111 111111111 111111111

但是char类型只有8个比特位，所以补码存起来就是111111111，而且第一位为符号位（对于a和b）

%d是10进制的形式打印有符号的整数

那么就需要进行整形提升（无符号数高位补0，有符号数高位补符号位）（对原码整形提升）

对于a和b：整形提升后补码为111111111 111111111 111111111 111111111（也就是-1）

对于c：整形提升后补码为00000000 00000000 00000000 111111111（又因为是无符号的整形，补码和原码一样）（也就是255）

---

 <2>下面程序输出什么？

#include 
int main()
{
	char a = -128;
	printf("%u\n", a);
	return 0;
}

答案：

4294967168

解释：

-128的原码：10000000 00000000 00000000 10000000

           反码：111111111 111111111 111111111 011111111

           补码：111111111 111111111 111111111 10000000

存进a的补码：10000000（1为符号位）

对a进行整形提升：111111111 111111111 111111111 10000000（有符号位高位补符号位1）

%u是10进制的形式打印无符号的整数

那么打印就当a是无符号数打印，对于无符号数原反补码相同，直接算即可

---

 <3>下面程序输出什么？

#include 
int main()
{
	char a = 128;
	printf("%u\n", a);
	return 0;
}

答案：

4294967168

解释：

虽然signed char最大只能是127，但是还是可以赋值为128，可以自行截断

128的原码：00000000 00000000 00000000 10000000

存进a的补码：10000000（1为符号位）

对a进行整形提升：111111111 111111111 111111111 10000000（有符号位高位补符号位1）

10进制无符号形式打印

---

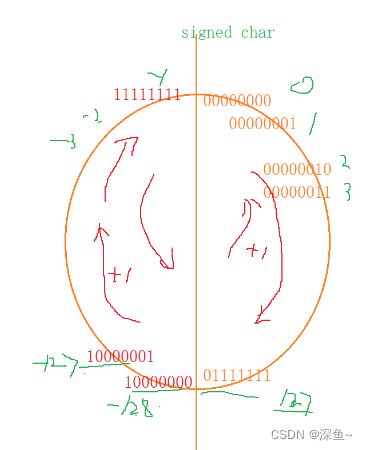
【总结】： 

signed char：-128~127

char-假设是有符号的char（1个字节=8bit） （第一位为符号位）第一列为原码

00000000   0

00000001   1

00000010   2

00000011   3

...                ...

011111111  127

10000000 -128  11111111（反） 110000000（补：多出来一位要删去）

10000001  -127  11111110           111111111

...

111111110  -2      10000001            10000010

111111111  -1      10000000            10000001

  

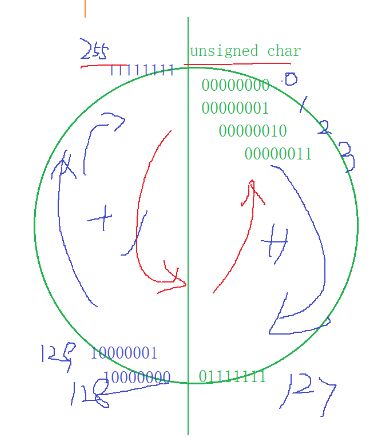
假设是unsigned char：0~255

 00000000

00000001   1

00000010   2

00000011   3

...                

011111111  127

10000000  128

...

111111110  254

111111111  255

---

  <4>下面程序输出什么？

int i= -20;
unsigned int j = 10;
printf("%d\n", i+j);

答案：

-10

解释：

-20：原码：10000000 00000000 00000000 00010100

         反码：111111111 111111111 111111111 11101011

         补码：111111111 111111111 111111111 11101100

10：原反补码：00000000 00000000 00000000 00001010（相加时最高位变为符号位）

补码进行相加：111111111 111111111 111111111 11110110（补码）

反码：10000000 00000000 00000000 00001001

原码：10000000 00000000 00000000 00001010（-10）

---

   <5>下面程序输出什么？

unsigned int i;
for(i = 9; i >= 0; i--)
{
printf("%u\n",i);
}

答案：

9到0再到4294967295，一直减小，死循环

解释：

unsigned int的范围就是>=0的，所以for循环的判断条件恒成立，类比unsigned char当0继续减小，就到了255，unsigned int也是这样的

---

    <6>下面程序输出什么？

int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));
return 0;
}

答案：

255

解释：

strlen是统计\0（也就是0）之前的字符个数

a[ i ]里面放的是-1，-2，-3...-128 127 ...6 5 4 3 2 1 0

一共就是128+127=255个数

---

     <7>下面程序输出什么？

#include 
unsigned char i = 0;
int main()
{
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0;
}

答案：

死循环

解释：

unsigned char的范围就是0-255，for循环的条件恒成立，进入死循环

---

三、浮点型在内存中的存储

常见的浮点数：

3.14159

1E10（也就是1.0*10^10)

浮点数家族包括：float，double，long double类型

浮点数表示的范围：float.h中定义

1.一个例子

int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为：%d\n",n);
printf("*pFloat的值为：%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为：%d\n",n);
printf("*pFloat的值为：%f\n",*pFloat);
return 0;
}

结果：

---

  2.浮点数存储规则

任意一个二进制浮点数V可以表示成下面的形式：

eg：10进制的5.5转化为二进制

101.1（小数点后面一位就是2的-1次方也就是0.5）

二进制浮点数表示也就是（-1）^0*1.011*2^2(小数点提前两位，也就是*2^2(二进制），如果是十进制就是2^10) 

得出：S=0，M=1.011，E=2

---

对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M
 

---

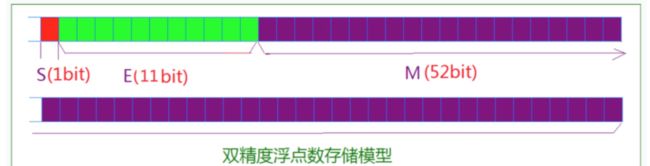
有效数字M的存储：

对于有效数字M，1<=M<2,在计算机内部保存M的时候，默认小数点前面一位为1，所以保存只保存小数点后面的数字，这样就节省了一位数的空间，以32位为例，虽然留给M只有23位，但是相当于保存了24位有效数字 

有效数字E的存储：

 首先E是一个为无符号数，如果E为8位，它的取值范围为0-255；如果E为11位，它的取值范围为0-2047。存入E的真实值时必须加上一个中间值，对于8位的E这个中间值为127，对于11的E，这个中间值为1023

eg：2^10的E为10，所以保存32位浮点数时，必须保存成10+127=137，即10001001

 指数E从内存中取出还可以再分成三种情况：

（1）E不全为0或不全为1：

指数E的计算值减去127（或1023），得到真实值，再将M小数点前面的1补上

eg：

0.5的二进制为0.1，浮点数表示：1.0*2^（-1），E存储为-1+127=126，也就是01111110，而尾数1.0去除1就是0，那么0.5的二进制表示形式就是：

0 01111110 00000000000000000000000

（2）E全为0：

这时浮点数的指数E等于1-127（或者1-1023）即为真实值

M这时也不需要加上小数点前面的1，而是还原成0.xxxx的小数，这样做是为了表示正负0，以及接近于0的很小的数

（3）E全为1：

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）

---

 现在再来解释一下前面的例子：

从int类型的9来看：

int n=9；

00000000 00000000 00000000 00001001（int类型二进制）

但是当它强制类型转化为float*时，代表的含义就不一样了

0 00000000 00000000000000000001001

这时的E为全0，那么E=-126，M也不用补0，即M=0.00000000000000000001001，S=0

那么*pFloat也就是（-1）^0*0.00000000000000000001001*2^(-126),这个数是极其小的，打印出来就直接是0.000000（float打印小数点后6位）

从float类型的9.0来看：（当*pFloat=9.0以后）

9.0（1001.0）

浮点型表示形式：(-1)^0*1.001*2^3

二进制表示：0 10000010 00100000000000000000

然后%d形式打印：n的视角看这是补码，符号位是0，为正数，原反补码相同，转化为10进制也就是1091567616

---

本次内容就到此啦，欢迎评论区或者私信交流，觉得笔者写的还可以，或者自己有些许收获的，麻烦铁汁们动动小手，给俺来个一键三连，万分感谢 !