数据挖掘——关联分析(关联规则产生)
基础概念
1、关联分析(association analysis):从大规模数据集中寻找商品的隐含关系;
2、项集 (itemset):包含0个或者多个项的集合称为项集
3、频繁项集:那些经常一起出现的物品集合
4、支持度计数(support count):一个项集出现的次数也就是整个交易数据集中包含该项集的事物数。
算法原理
Apriori算法找出所有可能是频繁项集的项集,即候选项集,然后根据最小支持度计数删选出频繁项集,最简单的办法是穷举法,即把每个项集都作为候选项集,统计他在数据集中出现的次数,如果出现次数大于最小支持度计数,则为频繁项集,分为两个步骤:
(1) 通过迭代,检索出事务数据集中的所有频繁项集,即支持度不低于用户设定的阈值的项集;
(2) 利用频繁项集构造出满足用户最小信任度的规则。其中,挖掘或识别出所有频繁项集是该算法的核心,占整个计算量的大部分。
当数据集很大的时候,Apriori算法需要不断扫描数据集造成运行效率很低。FP-Growth算法很好地解决了这个问题,其思路是将数据集中的事务映射到一棵FP-Tree上面,再根据这棵树找出频繁项集。FP-Tree的构建过程只需要扫描两次数据集。FP-growth算法分为三个过程:
(1) 找出频繁项的列表L,按照他们的支持度计数递减排序;
(2) 根据原始数据构造FP-Tree;
(3) 在FP-Tree上挖掘频繁模式。
实验内容
设事务集如下:
TID Items
001 :a,c,d,f,n
002 :b,c,d,e,f,i,k
003 :d,e,f,g,m
004 :b,f,p,s
005 :c,d,f,s
006 :a,b,c,e,h,o
1、设置相应的最小支持度阈值和最小置信度阈值,使用apyori库进行频繁项分析,并输出频繁项集与规则(附上支持度与置信度。)格式如下:
频繁项集:abc,支持度=20%;
产生的规则:ab->c,置信度=60%;
a->bc,置信度=60%
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from apyori import apriori
# 设置数据集
dataset = [['a', 'c', 'd', 'f', 'n'],
['b', 'c', 'd', 'e', 'f', 'i','k'],
['d', 'e', 'f', 'g','m'],
['b', 'f', 'p', 's'],
['c', 'd', 'f', 's']]
min_supp = 0.2 # 设定最小支持度
min_conf = 0.7 # 设定最小置信度
min_lift = 0.0 # 设定最小提升度
# 调用apriori方法,在这里不满足最小支持度、置信度和提升度的项集以及规则会被自动排除
res = apriori(transactions=dataset, min_support=min_supp, min_confidence=min_conf, min_lift=min_lift)
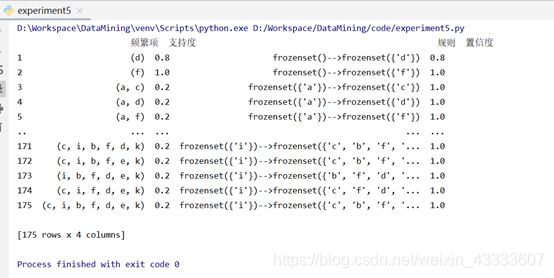
a=pd.DataFrame(columns=('频繁项','支持度','规则','置信度'))
i=1
for rule in res:
one= list(rule)
two = list(one[2])
three = list(two[0])
# print(str(three[0])+"-->"+str(three[1]))
row={'频繁项':one[0],'支持度':one[1],'规则':str(three[0])+"-->"+str(three[1]),'置信度':three[2]}
a.loc[i]=row
i=i+1
pd.set_option('display.max_columns', None)
pd.set_option('display.width',400) #x就是你要设置的显示的宽度,防止轻易换行
print(a)
 实验结果分析:
实验结果分析:
输入事务集,设置最小支持度及最小置信度阈值,调用apyori库中的apriori方法,在这里不满足最小支持度、置信度和提升度的项集以及规则会被自动排除,进而遍历Apriori后的结果得出频繁项以及频繁项的支持度,同时也产生达到最小置信度阈值的规则。
2、使用python实现Apriori算法,并使用同一数据集,分析频繁项结果
# 加载样本数据集
def load_data_set():
data_set = [['a', 'c', 'd', 'f', 'n'],
['b', 'c', 'd', 'e', 'f', 'i', 'k'],
['d', 'e', 'f', 'g', 'm'],
['b', 'f', 'p', 's'],
['c', 'd', 'f', 's']]
return data_set
# 得到数据集中的每个数据,且进行排序
def create_C1(data_set):
C1 = set()
for t in data_set:
for item in t:
item_set = frozenset([item])
C1.add(item_set)
return C1
def is_apriori(Ck_item, Lksub1):
for item in Ck_item:
sub_Ck = Ck_item - frozenset([item])
if sub_Ck not in Lksub1:
return False
return True
def create_Ck(Lksub1, k):
Ck = set()
len_Lksub1 = len(Lksub1)
list_Lksub1 = list(Lksub1)
for i in range(len_Lksub1):
for j in range(1, len_Lksub1):
l1 = list(list_Lksub1[i])
l2 = list(list_Lksub1[j])
l1.sort()
l2.sort()
if l1[0:k-2] == l2[0:k-2]:
Ck_item = list_Lksub1[i] | list_Lksub1[j]
if is_apriori(Ck_item, Lksub1):
Ck.add(Ck_item)
return Ck
def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
Lk = set()
item_count = {}
for t in data_set:
for item in Ck:
if item.issubset(t):
if item not in item_count:
item_count[item] = 1
else:
item_count[item] += 1
t_num = float(len(data_set))
for item in item_count:
if (item_count[item] / t_num) >= min_support:
Lk.add(item)
support_data[item] = item_count[item] / t_num
return Lk
def generate_L(data_set, k, min_support):
support_data = {}
C1 = create_C1(data_set)
L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
Lksub1 = L1.copy()
L = []
L.append(Lksub1)
for i in range(2, k+1):
Ci = create_Ck(Lksub1, i)
Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
Lksub1 = Li.copy()
L.append(Lksub1)
return L, support_data
def generate_big_rules(L, support_data, min_conf):
big_rule_list = [] # 存储所有的关联规则
sub_set_list = [] #
for i in range(0, len(L)): # 只获取2个或更多项集
for freq_set in L[i]:
# 遍历L中每一个频繁项集,对每个项集创建包含单个元素的列表
for sub_set in sub_set_list:
if sub_set.issubset(freq_set):
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf)
if conf >= min_conf and big_rule not in big_rule_list:
big_rule_list.append(big_rule)
sub_set_list.append(freq_set)
return big_rule_list
if __name__ == "__main__":
data_set = load_data_set()
L, support_data = generate_L(data_set, k=3, min_support=0.3)
big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
for Lk in L:
print("-"*50)
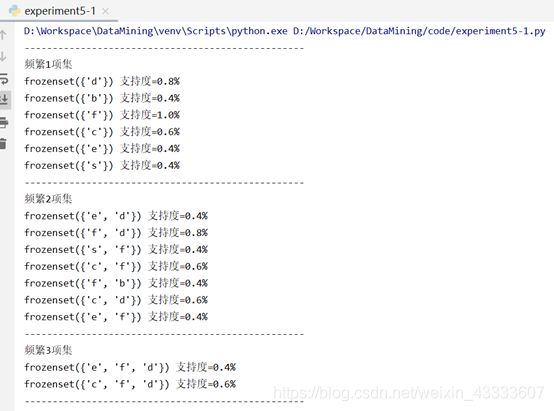
print("频繁" + str(len(list(Lk)[0])) + "项集")
for freq_set in Lk:
print(freq_set, "支持度=" + str(support_data[freq_set]) + "%")
print("-" * 50)
print("产生的规则:")
for item in big_rules_list:
print (item[0], "->", item[1], "置信度=" + str(item[2]) + "%")
print("-" * 50)