(十 三)特殊的二阶张量——反对称张量
本文主要内容如下:
- 1. 反对称二阶张量的概念
- 2. 反对称二阶张量的主不变量
- 3. 反对称二阶张量的特征值与特征向量
- 4. 反对称二阶张量的标准形
- 4. 反偶矢量
- 5. 反对称二阶张量对应的线性变换
1. 反对称二阶张量的概念
定义 若仿射量 Ω \bold{\Omega} Ω 满足:
Ω T = − Ω \bold{\Omega}^T=-\bold{\Omega} ΩT=−Ω
则称仿射量 Ω \bold{\Omega} Ω为反对称二阶张量(反称仿射量)。
2. 反对称二阶张量的主不变量
由于张量的主不变量不随坐标系的改变而改变,另外在笛卡尔坐标系中反对称张量 Ω \bold{\Omega} Ω的矩阵为反对称矩阵,记作:
[ 0 Ω 1 Ω 2 − Ω 1 0 Ω 3 − Ω 2 − Ω 3 0 ] \begin{bmatrix} 0&\Omega_1&\Omega_2\\\\ -\Omega_1&0&\Omega_3\\\\ -\Omega_2&-\Omega_3&0 \end{bmatrix} ⎣ ⎡0−Ω1−Ω2Ω10−Ω3Ω2Ω30⎦ ⎤
那么,
{ C 1 Ω = 0 C 2 Ω = Ω 1 2 + Ω 2 2 + Ω 3 2 ≜ φ 2 > 0 C 3 Ω = 0 × ( 0 + Ω 3 2 ) − ( − Ω 1 ) × ( 0 + Ω 3 Ω 2 ) + ( − Ω 2 ) × ( Ω 1 Ω 3 − 0 ) = 0 \begin{cases} \mathscr{C}^{\Omega}_1=0 \\\ \\ \mathscr{C}^{\Omega}_2={\Omega}_1^2+{\Omega}_2^2+{\Omega}_3^2\triangleq\varphi^2>0 \\\ \\ \mathscr{C}^{\Omega}_3=0\times(0+{\Omega}_3^2) -(-{\Omega}_1)\times(0+{\Omega}_3{\Omega}_2)+(-{\Omega}_2)\times({\Omega}_1{\Omega}_3-0)=0 \end{cases} ⎩ ⎨ ⎧C1Ω=0 C2Ω=Ω12+Ω22+Ω32≜φ2>0 C3Ω=0×(0+Ω32)−(−Ω1)×(0+Ω3Ω2)+(−Ω2)×(Ω1Ω3−0)=0
3. 反对称二阶张量的特征值与特征向量
反对称二阶张量 Ω \bold{\Omega} Ω的特征方程为:
λ 3 − C 1 Ω λ 2 + C 2 Ω λ − C 3 Ω = ( λ 2 + φ 2 ) λ = 0 \lambda^3-\mathscr{C}^{\Omega}_1\lambda^2+\mathscr{C}^{\Omega}_2\lambda-\mathscr{C}^{\Omega}_3=(\lambda^2+\varphi^2)\lambda=0 λ3−C1Ωλ2+C2Ωλ−C3Ω=(λ2+φ2)λ=0
因此,反对称二阶张量的特征值为:
λ 1 = i φ 、 λ 2 = − i φ 、 λ 3 = 0 \lambda_1=i\varphi、\lambda_2=-i\varphi、\lambda_3=0 λ1=iφ、λ2=−iφ、λ3=0
故,反对称张量的特征值由零与一对共轭纯虚数构成,虚部为反称仿射量第二主不变量的算术平方根。 又
( λ 1 u ⃗ 1 ) ∙ u ⃗ 3 = Ω ∙ u ⃗ 1 ∙ u ⃗ 3 = − u ⃗ 1 ∙ Ω ∙ u ⃗ 3 = − λ 3 u ⃗ 1 ∙ u ⃗ 3 ⟹ ( λ 1 + λ 3 ) u ⃗ 1 ∙ u ⃗ 3 = 0 ⟹ u ⃗ 1 ∙ u ⃗ 3 = 0 ( λ 2 u ⃗ 2 ) ∙ u ⃗ 3 = Ω ∙ u ⃗ 2 ∙ u ⃗ 3 = − u ⃗ 2 ∙ Ω ∙ u ⃗ 3 = − λ 3 u ⃗ 2 ∙ u ⃗ 3 ⟹ ( λ 2 + λ 3 ) u ⃗ 2 ∙ u ⃗ 3 = 0 ⟹ u ⃗ 2 ∙ u ⃗ 3 = 0 (\lambda_1\vec{u}_1)\bullet\vec{u}_3 =\Omega\bullet\vec{u}_1\bullet\vec{u}_3 =-\vec{u}_1\bullet\Omega\bullet\vec{u}_3 =-\lambda_3\vec{u}_1\bullet\vec{u}_3 \Longrightarrow (\lambda_1+\lambda_3)\vec{u}_1\bullet\vec{u}_3=0 \Longrightarrow \vec{u}_1\bullet\vec{u}_3=0\\\ \\ (\lambda_2\vec{u}_2)\bullet\vec{u}_3 =\Omega\bullet\vec{u}_2\bullet\vec{u}_3 =-\vec{u}_2\bullet\Omega\bullet\vec{u}_3 =-\lambda_3\vec{u}_2\bullet\vec{u}_3 \Longrightarrow (\lambda_2+\lambda_3)\vec{u}_2\bullet\vec{u}_3=0 \Longrightarrow \vec{u}_2\bullet\vec{u}_3=0 (λ1u1)∙u3=Ω∙u1∙u3=−u1∙Ω∙u3=−λ3u1∙u3⟹(λ1+λ3)u1∙u3=0⟹u1∙u3=0 (λ2u2)∙u3=Ω∙u2∙u3=−u2∙Ω∙u3=−λ3u2∙u3⟹(λ2+λ3)u2∙u3=0⟹u2∙u3=0
则,反对称二阶张量的实特征向量与共轭的复特征向量分别正交,即 u ⃗ 3 ∙ u ⃗ 1 = u ⃗ 3 ∙ u ⃗ 2 = 0 \vec{u}_3\bullet\vec{u}_1=\vec{u}_3\bullet\vec{u}_2=0 u3∙u1=u3∙u2=0
定义 将实特征值 λ 3 \lambda_3 λ3 特征方向 u ⃗ 3 \vec{u}_3 u3上的单位矢量 e ⃗ 3 \vec{e}_3 e3 称作 反对称张量 Ω \Omega Ω的轴。由于 Ω ∙ u ⃗ 3 = 0 ⟹ Ω ∙ e ⃗ 3 = Ω ∙ u ⃗ 3 ∣ u ⃗ 3 ∣ = 0 \Omega\bullet\vec{u}_3=0\Longrightarrow\Omega\bullet\vec{e}_3=\Omega\bullet\frac{\vec{u}_3}{|\vec{u}_3|}=0 Ω∙u3=0⟹Ω∙e3=Ω∙∣u3∣u3=0故,反对称张量将其轴方向上的任何向量映射为零向量。
4. 反对称二阶张量的标准形
- 若以反对称张量的三个线性无关的特征向量为基,则有:
Ω = ( i φ ) u ⃗ 1 u ⃗ 1 − ( i φ ) u ⃗ 2 u ⃗ 2 \bold{\Omega}=(i\varphi)\vec{u}_1\vec{u}^1-(i\varphi)\vec{u}_2\vec{u}^2 Ω=(iφ)u1u1−(iφ)u2u2 - 若按照一般的处理方式由复数对角标准形得到实数标准形,取
{ g ⃗ 1 = u ⃗ 1 + u ⃗ 2 g ⃗ 2 = i ( u ⃗ 1 − u ⃗ 2 ) g ⃗ 3 = e 3 \begin{cases} \vec{g}_1=\vec{u}_1+\vec{u}_2\\\\ \vec{g}_2=i(\vec{u}_1-\vec{u}_2)\\\\ \vec{g}_3=e_3 \end{cases} ⎩ ⎨ ⎧g1=u1+u2g2=i(u1−u2)g3=e3
则有:
Ω = − φ g ⃗ 1 g ⃗ 2 + φ g ⃗ 2 g ⃗ 1 \bold{\Omega}=-\varphi\vec{g}_1\vec{g}^2+\varphi\vec{g}_2\vec{g}^1 Ω=−φg1g2+φg2g1
值得注意的是,反对称张量实数化标准形所参考的基 { g ⃗ 1 、 g ⃗ 2 、 g ⃗ 3 } \{\vec{g}_1、\vec{g}_2、\vec{g}_3\} {g1、g2、g3}具有正交性,因为根据反对称张量实特征向量与复特征向量之间的正交性知:
g ⃗ 3 ∙ g ⃗ 1 = u ⃗ 3 ∣ u ⃗ 3 ∣ ∙ ( u ⃗ 1 + u ⃗ 2 ) = 0 ( a ) g ⃗ 3 ∙ g ⃗ 2 = i u ⃗ 3 ∣ u ⃗ 3 ∣ ∙ ( u ⃗ 1 − u ⃗ 2 ) = 0 ( b ) \vec{g}_3\bullet\vec{g}_1=\frac{\vec{u}_3}{|\vec{u}_3|}\bullet(\vec{u}_1+\vec{u}_2)=0\qquad(a)\\\ \\ \vec{g}_3\bullet\vec{g}_2=i\frac{\vec{u}_3}{|\vec{u}_3|}\bullet(\vec{u}_1-\vec{u}_2)=0\qquad(b) g3∙g1=∣u3∣u3∙(u1+u2)=0(a) g3∙g2=i∣u3∣u3∙(u1−u2)=0(b)
此外,由于对于任意向量 x ⃗ \vec{x} x,向量 Ω ∙ x ⃗ \bold{\Omega}\bullet\vec{x} Ω∙x 或 x ⃗ ∙ Ω \vec{x}\bullet\bold{\Omega} x∙Ω均与其正交,即 x ⃗ ∙ Ω ∙ x ⃗ = x i Ω i j x j = x j Ω j i x i = − x j Ω i j x i ⟹ x i Ω i j x j = x ⃗ ∙ Ω ∙ x ⃗ = 0 \vec{x}\bullet\bold{\Omega}\bullet\vec{x}=x^i\Omega_{ij}x^j=x^j\Omega_{ji}x^i=-x^j\Omega_{ij}x^i\Longrightarrow x^i\Omega_{ij}x^j=\vec{x}\bullet\bold{\Omega}\bullet\vec{x}=0 x∙Ω∙x=xiΩijxj=xjΩjixi=−xjΩijxi⟹xiΩijxj=x∙Ω∙x=0
那么:
g ⃗ 1 ∙ Ω ∙ g ⃗ 1 = g ⃗ 1 ∙ ( − φ g ⃗ 1 g ⃗ 2 + φ g ⃗ 2 g ⃗ 1 ) ∙ g ⃗ 1 = φ g ⃗ 1 ∙ g ⃗ 2 = 0 ⟹ g ⃗ 1 ∙ g ⃗ 2 = 0 ( c ) \vec{g}_1\bullet\bold{\Omega}\bullet\vec{g}_1 =\vec{g}_1\bullet(-\varphi\vec{g}_1\vec{g}^2+\varphi\vec{g}_2\vec{g}^1)\bullet\vec{g}_1 =\varphi\vec{g}_1\bullet\vec{g}_2=0 \Longrightarrow \vec{g}_1\bullet\vec{g}_2=0\qquad(c) g1∙Ω∙g1=g1∙(−φg1g2+φg2g1)∙g1=φg1∙g2=0⟹g1∙g2=0(c)
另外,
g ⃗ 1 ∙ Ω ∙ g ⃗ 2 = − φ g ⃗ 1 ∙ g ⃗ 1 g ⃗ 2 ∙ Ω ∙ g ⃗ 1 = φ g ⃗ 2 ∙ g ⃗ 2 g ⃗ 1 ∙ Ω ∙ g ⃗ 2 = ( Ω ∙ g ⃗ 2 ) ∙ g ⃗ 1 = − g ⃗ 2 ∙ Ω ∙ g ⃗ 1 \vec{g}_1\bullet\bold{\Omega}\bullet\vec{g}_2=-\varphi\vec{g}_1\bullet\vec{g}_1\\\ \\ \vec{g}_2\bullet\bold{\Omega}\bullet\vec{g}_1=\varphi\vec{g}_2\bullet\vec{g}_2\\\ \\ \vec{g}_1\bullet\bold{\Omega}\bullet\vec{g}_2 =(\bold{\Omega}\bullet\vec{g}_2)\bullet\vec{g}_1 =- \vec{g}_2\bullet\bold{\Omega}\bullet\vec{g}_1 g1∙Ω∙g2=−φg1∙g1 g2∙Ω∙g1=φg2∙g2 g1∙Ω∙g2=(Ω∙g2)∙g1=−g2∙Ω∙g1
这说明:
∣ g ⃗ 1 ∣ = ∣ g ⃗ 2 ∣ ( d ) |\vec{g}_1|=|\vec{g}_2|\qquad (d) ∣g1∣=∣g2∣(d) - 实际上,在标准正交基 { e ⃗ 1 , e ⃗ 2 , e ⃗ 3 } \{\vec{e}_1,\vec{e}_2,\vec{e}_3\} {e1,e2,e3}( e ⃗ 1 , e ⃗ 2 \vec{e}_1,\vec{e}_2 e1,e2为 g ⃗ 1 \vec{g}_1 g1、 g ⃗ 2 \vec{g}_2 g2所张成平面内的任意相互正交的两个单位向量)反对称二阶张量 Ω \bold{\Omega} Ω均可展开为: Ω = − φ e ⃗ 1 e ⃗ 2 + φ e ⃗ 2 e ⃗ 1 \bold{\Omega}=-\varphi\vec{e}_1\vec{e}_2+\varphi\vec{e}_2\vec{e}_1 Ω=−φe1e2+φe2e1下面进行相关说明:
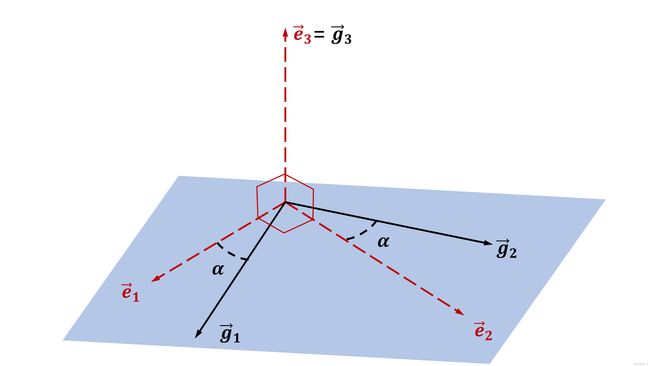
在垂直于 e ⃗ 3 \vec{e}_3 e3的平面内任意选择两互相正交的单位矢量 e ⃗ 1 \vec{e}_1 e1、 e ⃗ 2 \vec{e}_2 e2,并以 e ⃗ 1 \vec{e}_1 e1、 e ⃗ 2 \vec{e}_2 e2、 e ⃗ 3 \vec{e}_3 e3为一组新基,那么逆变转换系数为: [ β j i ′ ] = [ ∣ g ⃗ 1 ∣ c o s α − ∣ g ⃗ 2 ∣ s i n α 0 ∣ g ⃗ 1 ∣ s i n α ∣ g ⃗ 2 ∣ c o s α 0 0 0 1 ] [\beta^{i'}_j]=\begin{bmatrix} |\vec{g}_1|cos\alpha & -|\vec{g}_2|sin\alpha & 0 \\ \\ |\vec{g}_1|sin\alpha & |\vec{g}_2|cos\alpha & 0 \\ \\ 0 & 0 &1 \end{bmatrix} [βji′]=⎣ ⎡∣g1∣cosα∣g1∣sinα0−∣g2∣sinα∣g2∣cosα0001⎦ ⎤协变转换系数矩阵: [ β i ′ j ] = [ β j i ′ ] − 1 = [ ∣ g ⃗ 2 ∣ c o s α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ ∣ g ⃗ 2 ∣ s i n α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ 0 − ∣ g ⃗ 1 ∣ s i n α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ ∣ g ⃗ 1 ∣ c o s α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ 0 0 0 1 ] [\beta_{i'}^j]=[\beta^{i'}_j]^{-1}=\begin{bmatrix} \frac{ |\vec{g}_2|cos\alpha}{|\vec{g}_1||\vec{g}_2|} & \frac{ |\vec{g}_2|sin\alpha}{|\vec{g}_1||\vec{g}_2|} & 0 \\ \\ \frac{ -|\vec{g}_1|sin\alpha}{|\vec{g}_1||\vec{g}_2|} & \frac{ |\vec{g}_1|cos\alpha}{|\vec{g}_1||\vec{g}_2|} & 0 \\ \\ 0 & 0 &1 \end{bmatrix} [βi′j]=[βji′]−1=⎣ ⎡∣g1∣∣g2∣∣g2∣cosα∣g1∣∣g2∣−∣g1∣sinα0∣g1∣∣g2∣∣g2∣sinα∣g1∣∣g2∣∣g1∣cosα0001⎦ ⎤那么根据坐标转换关系,在新基中反对称张量的分量为: [ Ω ∙ n ′ m ′ ] = [ ∣ g ⃗ 1 ∣ c o s α − ∣ g ⃗ 2 ∣ s i n α 0 ∣ g ⃗ 1 ∣ s i n α ∣ g ⃗ 2 ∣ c o s α 0 0 0 1 ] [ 0 − φ 0 φ 0 0 0 0 0 ] [ ∣ g ⃗ 2 ∣ c o s α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ ∣ g ⃗ 2 ∣ s i n α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ 0 − ∣ g ⃗ 1 ∣ s i n α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ ∣ g ⃗ 1 ∣ c o s α ∣ g ⃗ 1 ∣ ∣ g ⃗ 2 ∣ 0 0 0 1 ] = [ 0 − φ 0 φ 0 0 0 0 0 ] [\Omega^{m'}_{\bullet n'}]=\begin{bmatrix} |\vec{g}_1|cos\alpha & -|\vec{g}_2|sin\alpha & 0 \\ \\ |\vec{g}_1|sin\alpha & |\vec{g}_2|cos\alpha & 0 \\ \\ 0 & 0 &1 \end{bmatrix} \begin{bmatrix} 0 & -\varphi & 0 \\\\ \varphi & 0& 0 \\\\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} \frac{ |\vec{g}_2|cos\alpha}{|\vec{g}_1||\vec{g}_2|} & \frac{ |\vec{g}_2|sin\alpha}{|\vec{g}_1||\vec{g}_2|} & 0 \\ \\ \frac{ -|\vec{g}_1|sin\alpha}{|\vec{g}_1||\vec{g}_2|} & \frac{ |\vec{g}_1|cos\alpha}{|\vec{g}_1||\vec{g}_2|} & 0 \\ \\ 0 & 0 &1 \end{bmatrix}= \begin{bmatrix} 0 & -\varphi & 0 \\\\ \varphi & 0& 0 \\\\ 0 & 0 & 0 \end{bmatrix} [Ω∙n′m′]=⎣ ⎡∣g1∣cosα∣g1∣sinα0−∣g2∣sinα∣g2∣cosα0001⎦ ⎤⎣ ⎡0φ0−φ00000⎦ ⎤⎣ ⎡∣g1∣∣g2∣∣g2∣cosα∣g1∣∣g2∣−∣g1∣sinα0∣g1∣∣g2∣∣g2∣sinα∣g1∣∣g2∣∣g1∣cosα0001⎦ ⎤=⎣ ⎡0φ0−φ00000⎦ ⎤可见,在所选的新标准正交基 { e ⃗ 1 , e ⃗ 2 , e ⃗ 3 } \{\vec{e}_1,\vec{e}_2,\vec{e}_3\} {e1,e2,e3}中各分量与原来的正交基 { g ⃗ 1 , g ⃗ 2 , g ⃗ 3 } \{\vec{g}_1,\vec{g}_2,\vec{g}_3\} {g1,g2,g3}中相同。(证毕)
4. 反偶矢量
定义
ω ⃗ = − 1 2 ϵ : Ω = − 1 2 Ω : ϵ \vec{\omega}=-\frac{1}{2}\bold{\epsilon}:\bold{\Omega}=-\frac{1}{2}\bold{\Omega}:\bold{\epsilon} ω=−21ϵ:Ω=−21Ω:ϵ
称 ω ⃗ \vec{\omega} ω 为反对称二阶张量 Ω \bold{\Omega} Ω 的反偶矢量,或 − ω ⃗ -\vec{\omega} −ω与 Ω \bold{\Omega} Ω 互为对偶。
按照定义: ω ⃗ = − 1 2 ϵ : ( − φ e ⃗ 1 e ⃗ 2 + φ e ⃗ 2 e ⃗ 1 ) = 1 2 φ ( e ⃗ 1 × e ⃗ 2 − e ⃗ 2 × e ⃗ 1 ) = φ e ⃗ 3 \vec{\omega} =-\frac{1}{2}\bold{\epsilon}:(-\varphi\vec{e}_1\vec{e}_2+\varphi\vec{e}_2\vec{e}_1) =\frac{1}{2}\varphi(\vec{e}_1\times\vec{e}_2-\vec{e}_2\times\vec{e}_1) =\varphi\vec{e}_3 ω=−21ϵ:(−φe1e2+φe2e1)=21φ(e1×e2−e2×e1)=φe3说明,对偶矢量沿反对称张量的轴向,大小为 φ = C 2 Ω \varphi=\sqrt{\mathscr{C}^{\Omega}_2} φ=C2Ω。
另外反对称张量可由其对偶矢量得到,证明如下: ω k g ⃗ k = − 1 2 ϵ : Ω i j g ⃗ i g ⃗ j = − 1 2 ( g ⃗ i × g ⃗ j ) Ω i j = − 1 2 ϵ i j k Ω i j g ⃗ k \omega_k\vec{g}^k =-\frac{1}{2}\bold{\epsilon}:\Omega^{ij}\vec{g}_i\vec{g}_j =-\frac{1}{2}(\vec{g}_i\times\vec{g}_j)\Omega^{ij} =-\frac{1}{2}\epsilon_{ijk}\Omega^{ij}\vec{g}^k ωkgk=−21ϵ:Ωijgigj=−21(gi×gj)Ωij=−21ϵijkΩijgk则 − ϵ ∙ ω ⃗ = ϵ p q l g ⃗ p g ⃗ q g ⃗ l ∙ 1 2 ϵ i j k Ω i j g ⃗ k = 1 2 ϵ i j l ϵ p q l Ω i j g ⃗ p g ⃗ q = 1 2 ( δ i p δ j q − δ j p δ i q ) Ω i j g ⃗ p g ⃗ q = 1 2 ( Ω − Ω T ) = Ω -\bold{\epsilon}\bullet\vec{\omega} =\epsilon^{pql}\vec{g}_p\vec{g}_q\vec{g}_l\bullet\frac{1}{2}\epsilon_{ijk}\Omega^{ij}\vec{g}^k =\frac{1}{2}\epsilon_{ijl}\epsilon^{pql}\Omega^{ij}\vec{g}_p\vec{g}_q =\frac{1}{2}(\delta^p_i\delta^q_j-\delta^p_j\delta^q_i)\Omega^{ij}\vec{g}_p\vec{g}_q =\frac{1}{2}(\bold{\Omega}-\bold{\Omega}^T) =\bold{\Omega} −ϵ∙ω=ϵpqlgpgqgl∙21ϵijkΩijgk=21ϵijlϵpqlΩijgpgq=21(δipδjq−δjpδiq)Ωijgpgq=21(Ω−ΩT)=Ω这意味着反对称张量只用给出其反偶矢量便可得到其所有的信息。
5. 反对称二阶张量对应的线性变换
由于 Ω ∙ u ⃗ = ( − ϵ ∙ ω ⃗ ) ∙ u ⃗ = − ϵ : ( u ⃗ ω ⃗ ) = − u ⃗ × ω ⃗ = ω ⃗ × u ⃗ u ⃗ ∙ Ω = u ⃗ ∙ ( − ϵ ∙ ω ⃗ ) = − u i ϵ i j k w k g ⃗ j = u i w k ϵ i k j g ⃗ j = u ⃗ × ω ⃗ \begin{aligned} &\bold{\Omega}\bullet\vec{u} =(-\bold{\epsilon}\bullet\vec{\omega})\bullet\vec{u} =-\bold{\epsilon}:(\vec{u}\vec{\omega}) =-\vec{u}\times\vec{\omega} =\vec{\omega}\times\vec{u} \\ \\ &\vec{u}\bullet\bold{\Omega} =\vec{u}\bullet(-\bold{\epsilon}\bullet\vec{\omega}) =-u^i\epsilon_{ijk}w^k\vec{g}^j =u^iw^k\epsilon_{ikj}\vec{g}^j =\vec{u}\times\vec{\omega} \end{aligned} Ω∙u=(−ϵ∙ω)∙u=−ϵ:(uω)=−u×ω=ω×uu∙Ω=u∙(−ϵ∙ω)=−uiϵijkwkgj=uiwkϵikjgj=u×ω这说明反对称张量将任意向量 u ⃗ \vec{u} u 映射为其对偶矢量与该向量的叉积。另外从几何上对反对称二阶张量定义的线性变换进行说明:
对于任意向量 u ⃗ = u 1 e ⃗ 1 + u 2 e ⃗ 2 + u 3 e ⃗ 3 \vec{u}=u_1\vec{e}_1+u_2\vec{e}_2+u_3\vec{e}_3 u=u1e1+u2e2+u3e3 有:
Ω = − φ e ⃗ 1 e ⃗ 2 + φ e ⃗ 2 e ⃗ 1 Ω ∙ u ⃗ = φ ( u 1 e ⃗ 2 − u 2 e ⃗ 1 ) u ⃗ ∙ Ω = φ ( − u 1 e ⃗ 2 + u 2 e ⃗ 1 ) \bold{\Omega}=-\varphi\vec{e}_1\vec{e}_2+\varphi\vec{e}_2\vec{e}_1\\\ \\ \bold{\Omega}\bullet\vec{u} =\varphi(u_1\vec{e}_2- u_2\vec{e}_1) \\\ \\ \vec{u}\bullet\bold{\Omega} =\varphi(-u_1\vec{e}_2+ u_2\vec{e}_1) Ω=−φe1e2+φe2e1 Ω∙u=φ(u1e2−u2e1) u∙Ω=φ(−u1e2+u2e1)
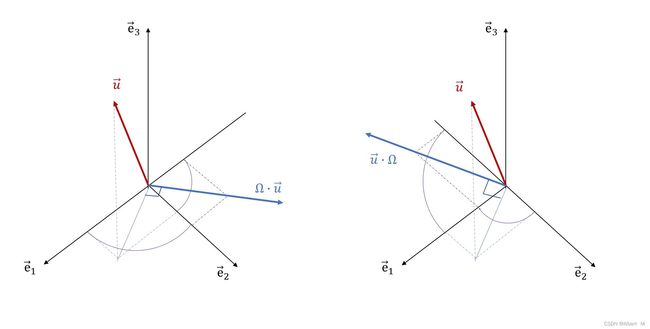
如图所示:
这意味着,
Ω ∙ u ⃗ \bold{\Omega}\bullet\vec{u} Ω∙u:将1-2面内的 u ⃗ \vec{u} u 分量绕轴按右手系旋转 90 ° 90° 90°并放大 φ = C 2 Ω \varphi=\sqrt{\mathscr{C}^{\Omega}_2} φ=C2Ω 倍,舍弃面外分量;
u ⃗ ∙ Ω \vec{u}\bullet\bold{\Omega} u∙Ω:将1-2面内的 u ⃗ \vec{u} u 分量绕轴按左手系旋转 90 ° 90° 90°并放大 φ \varphi φ 倍,舍弃面外分量;
上述关于二阶反对称张量线性变换的讨论也从几何上说明了 u ⃗ ∙ Ω ∙ u ⃗ = 0 \vec{u}\bullet\bold{\Omega}\bullet\vec{u}=0 u∙Ω∙u=0。