【二等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「Aries」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。
本方案为【大规模金融图数据中异常风险行为模式挖掘】赛题的二等奖获奖方案,赛题地址:https://www.datafountain.cn/competitions/586
获奖团队简介
团队名称:Aries
团队成员:本团队属校企联合团队,由江苏电信和北京师范大学组成,主要研究方向包括数据挖掘,云原生,AI,应用统计分析等,团队具有一定的项目经历和比赛经验。
所获奖项:二等奖
摘 要
随着图数据的日益普及,图挖掘已成为图分析的一项基本任务,其中频繁子图及模式挖掘作为重要一环已经被广泛应用在各个领域。在这个方向已经有大量的文献被发表,并取得了巨大的进步。随着频繁模式挖掘的深入研究,图模型被广泛地应用于为各种事务建模,因此图挖掘的研究显得越来越重要。
针对本赛题要求,本文主要做了以下四个方面工作:1、挖掘出满足阈值要求的的频繁模式。2、精确计算模式频繁的频繁度。3、面向数据编程,尽可能优化程序处理时间。4、使用OpenMP多线程框架,使程序在各个阶段的性能都得到优化。根据本队伍实际执行结果证明上述处理过程可以快速解决问题。
关 键 词
频繁子图,模式挖掘,频繁度
1 背景介绍
1.1 频繁子图挖掘介绍
频繁子图挖掘是数据挖掘中一个非常广泛的应用。频繁子图挖掘是指从大量的图中挖掘出满足给定支持度的频繁子图,同时算法需要保证这些频繁图不能重复。频繁模式挖掘主要就是应用两种策略——Apriori和Growth。最早的AGM和FSG就分别实现了这两重策略的基本思想。gSpan是一个非常高效的算法,它利用dfs-code序列对搜索树进行编码,并且制定一系列比较规则,从而保证最后只得到序列“最小”的频繁图集合。在频繁模式挖掘算法中,常用方法是先计算候选模式的可能性空间,再确定频繁度,由于查找子图模式需要判断子图同构,而判断子图同构是NP完全问题[1],因此计算代价非常大。基于单一大图频繁子图挖掘、频繁图模式挖掘算法GRAMI[2]可以利用多种巧妙的剪枝算法提升挖掘性能。子图生成过程中采用了GSAPN中的最右路扩展,从而保证了搜索空间是完备的。在计算图的支持度时,理论上也是精确的。但算法也提供了支持度的近似算法,近似算法保证了挖掘的子图一定是频繁的,但不是所有频繁的子图都能获得,如果要获得所有频繁子图需要调整支持度大小。
1.2 本题方案简介
本赛题使用简化的金融仿真数据,数据带有时间戳和金额的账户间交易、转账等数据。基于此数据自动挖掘出不小于频繁度(f >= 10000)的频繁子图模式集合。判定子图同构的方法需要属性值匹配,包括交易金额、策略名、业务编码及名称。子图只需匹配到3阶(3条边)子图,频繁度指标需满足单调性要求。
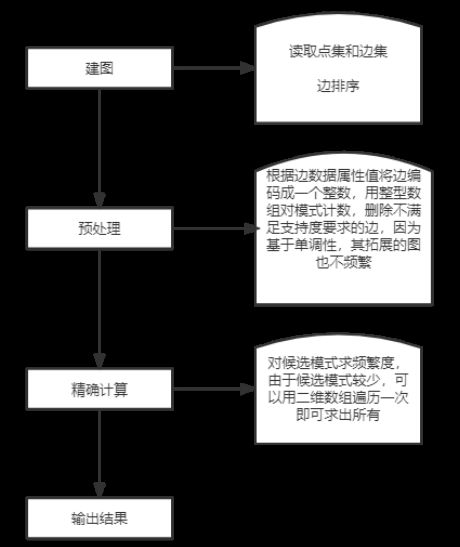
本方案主要将频繁子图挖掘分为两个个阶段:1:剪枝阶段。按题目模式匹配的要求计算出每条边的频繁度,根据单调性要求,将不满足支持度的边去掉,可以为后面挖掘二阶三阶子图省去大量无效遍历。2:精确计算频繁度阶段。利用近似的频繁模式,根据单调性要求,精确计算出满足阈值要求的模式频繁度。具体流程图见图1.
图1
2 算法设计与实现
我们将整体流程细分为5个步骤,分别是输入、构图、剪枝、频繁度计算和输出。首先,需要将数据文检读取进内存,用方便读取的数据结构存储,因为是有向图需要用偏移范围作索引,可以实现根据边起点的随机遍历。之后利用边数据属性值将边编码成一个整数,用整型数组对模式计数,删除不满足支持度要求的边,因为基于单调性,其拓展的图也不频繁。这样可以大大缩小了边的数据规模。对候选模式求频繁度,由于候选模式较少,可以用二维数组遍历一次即可求出所有模式的频繁度。在输入、构图、剪枝和频繁度四个阶段都是用OpenMP并行处理,大大提高了程序运行效率。
2.1 输入和构图
输入部分主要是从点数据文件和边数据文件读入数据,数据约748MB,因为数据量较大,读数据需要花很多时间,因此需要提高文件读取速度,我们团队采用mmap系统调用的方法读取文件,将数据存储到数组中。由于本赛题不仅考察答案的准确率,相同答案的情况下程序的运行时间也作为考察依据,为了加速文件读取速度,我们采用多线程读取,使用mmap映射后,根据文件的首地址和文件长度,按照字节长度将文件分配到多个任务中。上述为点数据的读取。
struct Edge {
uint32_t to;
uint32_t amt;
uint32_t strategy;
uint32_t buscode;
} *edges;
uint32_t *loc;
边数据读取较为特殊,为了能方便后续算法根据起点可以快速遍历,首先用多线程遍历一次边文件,将每个线程计算出的起点边数和汇总在一个数组loc中,这样若搜索定点s的边的时候,其边的范围就是[loc[s],loc[s+1]]。结构体中只存边的属性和目标点的信息。
2.2 剪枝
读取的原始数据中,很多边是不能满足频繁度要求的,根据单调性的约束,这些边的拓展边也不会满足单调性约束,所以需要将这些无效边删除,这样可以加速后续的处理。本方案使用flag数组标记边的有效性,遍历时遇到无效边,就直接跳过。为了高效计数,我们没有使用dfs-code编码,而是根据边的属性映射到整数上,通过一个整型数组作为计数器。例如一条边的属性为{from:1,to:1,aim:0,strategy:1,buscode:1},由于顶点只有3种类型(account_to_card可以用strategy区分),amt通过剪枝后有10种,strategy有6种,buscode有4种,这条边可以描述为1*3*10*6*4+1*10*6*4+0*6*4+6*4+4,所有边都可以通过此方法映射到对应的整数上。这里有个提升性能的方法,在不影响正确结果的情况下,可以适当将调整阈值调大,不过这样会导致和GRAMI[2]算法同样的问题,如果将阈值调整过大,只能保证挖掘的子图一定是频繁的,但不是所有频繁的子图都能获得,所以要根据图调整。
2.3 三阶边频繁度计算
三阶频繁度计算就是根据单调性的约束和阈值约束,求出满足条件的模式的频繁度。通过上述对一阶边的剪枝,可以将剩下的边继续拓展到二阶三阶中,也利用单调性和阈值的约束计算,但由于在处理三阶边的时候数值过大,无法将编码映射到整数中,所以在剪枝后要将边的值重新映射到数组中。重新映射后三阶边也可以映射到数据中,映射方式和一条边类似。这样就可以求出满足条件模式的频繁度。
2.4 输出
将计算出的结果使用fastjosn输出到文件中,输出时间占比较少,所以没用多线程处理。
3 实验结果
程序测试的物理机配置为4核 3.4Ghz服务器,操作系统为ubuntu20.04。我们对程序的各个阶段4个线程和单线程进行了比较,结果如下图2,多线程在各个阶段都显著提高运行速度,整个程序在4个线程下只需要执行0.92s,当然这是本地测试环境的结果,由于硬件配置不同,与线上结果有一些差别。
图2
致谢
感谢赛事的所有工作人员,他们默默无闻的努力,无微不至的付出,是支撑大赛顺利运行的坚定基石。感谢队友的努力付出,才能让我们团队进入最终决赛。
参考
[1] Wernicke S. Rasche F. FANMOD: A tool for fast network motif detection. Bioinformatics. 2006. 22(9) : 1152-1153
[2] GraMi:frequent subgraph and pattern mining in a single large graph [J] . Elseidy Mohammed,Abdelhamid Ehab,Skiadopoulos Spiros,Kalnis Panos. Proceedings of the VLDB Endowment . 2014 (7)
我是行业领先的大数据竞赛平台 @DataFountain ,欢迎广大政企校军单位合作办赛,推动优秀数据人才揭榜挂帅!