MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测|附代码数据

全文链接：http://tecdat.cn/?p=24211

最近我们被客户要求撰写关于GARCH的研究报告，包括一些图形和统计输出。

使用 garch 指定一个单变量GARCH（广义自回归条件异方差）模型（ 点击文末“阅读原文”获取完整代码数据）。

garch 模型的关键参数包括：

GARCH 多项式，由滞后条件方差组成。阶数用_P_表示。
ARCH多项式，由滞后平方组成。阶数用_Q_表示。

P 和 Q 分别是 GARCH 和 ARCH 多项式中的最大非零滞后。其他模型参数包括平均模型偏移、条件方差模型常数和分布。

所有系数都是未知（NaN 值）和可估计的。

示例： 'ARCHLags',[1 4],'ARCH',{NaN NaN} 指定 GARCH(0,4) 模型和未知但非零的 ARCH 系，滞后 1 和 4。

例子

创建默认 GARCH 模型

创建默认 garch 模型对象并指定其参数值。

创建 GARCH(0,0) 模型。

garch

Md 是一个 garch 模型。它包含一个未知常数，其偏移量为 0，分布为 'Gaussian'。该模型没有 GARCH 或 ARCH 多项式。

为滞后 1 和滞后 2 指定两个未知的 ARCH 系数。

ARCH = {NN NN}

该 Q 和 ARCH 性能更新为 2 和 {NaN NaN}。两个 ARCH 系数与滞后 1 和滞后 2 相关联。

创建 GARCH 模型

garch 创建模型 garch(P,Q)，其中 P 是 GARCH 多项式的阶数， Q 是 ARCH 多项式的阶数。

创建 GARCH(3,2) 模型

garch(3,2)

Md 是一个 garch 模型对象。 Md的所有属性，除了 P， Q和 Distribution，是 NaN 值。默认情况下：

包括条件方差模型常数
排除条件平均模型偏移（即偏移为 0）
包括 ARCH 和 GARCH 滞后运算符多项式中的所有滞后项，分别达到滞后 Q 和 P。

Md仅指定 GARCH 模型的函数形式。因为它包含未知的参数值，您可以通过 Md 和时间序列数据 estimate 来估计参数。

使用参数创建 GARCH 模型

garch 使用名称-值对参数创建模型。

指定 GARCH(1,1) 模型。默认情况下，条件平均模型偏移为零。指定偏移量为 NaN。

grch('GRCHas',1,'CHLas',1,'Oset',aN)

Md 是一个 garch 模型对象。

由于 Md包含 `NaN` 值， Md仅适用于估计。将 `Md时间序列数据传递给 estimate`.

创建具有已知系数的 GARCH 模型

创建一个具有平均偏移量的 GARCH(1,1) 模型，

yt=0.5+εt,

其中 εt=σtzt，

σ2t = 0.0001 + 0.75σ2t − 1 + 0.1ε2t − 1，

zt 是一个独立同分布的标准高斯过程。

 garh('Conant',00001,'GACH',0.75,...
    'AR H ,0.1,'Ofet'0.5)

访问 GARCH 模型属性

创建 garch 模型对象。

 garch(3,2)

从模型中删除第二个 GARCH 项。即，指定第二个滞后条件方差的 GARCH 系数为 0。

GAH{2} = 0

GARCH 多项式有两个未知参数，分别对应滞后 1 和滞后 3。

显示扰动的分布。

Ditiuton

扰动是均值为 0 且方差为 1 的高斯扰动。

指定基础 IID 扰动具有五个自由度的_t_分布。

dl.Dirbton = trut('Nme','t','DF',5)

指定第一个滞后的 ARCH 系数为 0.2，第二个滞后的 ARCH 系数为 0.1。

ACH = {0.2 0.1}

要估计残差的参数，您可以将`Md数据传递给 estimate 指定的参数并将其用作等式约束。或者，您可以指定其余的参数值，然后通过将完全指定的模型分别传递给simulate 或来模拟或预测 GARCH 模型的条件方差 forecast`。

估计 GARCH 模型

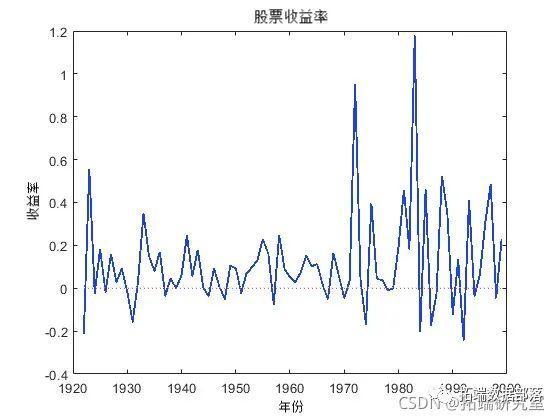
将 GARCH 模型拟合到 1922-1999 年股票收益率的年度时间序列。

加载 Data数据集。绘制收益率 ( nr)。

RN;

fiure;
plot(daes,nr;
hod n;
pot([dtes(1) dtes(n

收益序列似乎具有非零条件平均偏移，并且似乎表现出波动聚集。也就是说，较早年份的变异性小于晚年的变异性。对于此示例，假设 GARCH(1,1) 模型适用于该序列。

点击标题查阅往期内容

R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

左右滑动查看更多

创建 GARCH(1,1) 模型。默认情况下，条件平均偏移为零。要估计偏移量，请将其指定为 NaN。

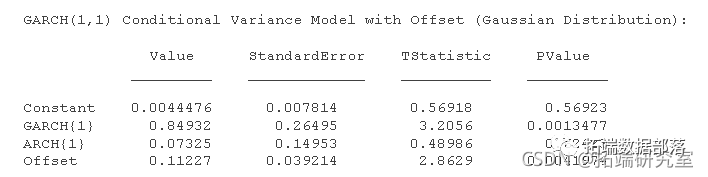
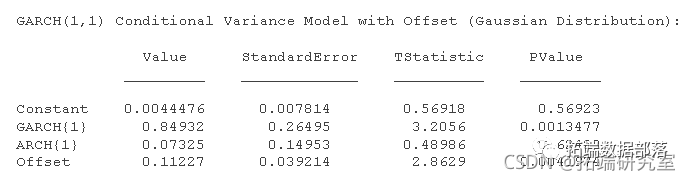
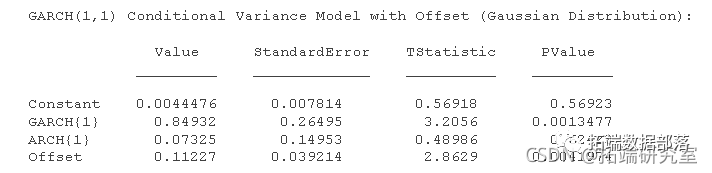
garh('GCHags',1,'ARHLgs',1,'Ofst',Na);

将 GARCH(1,1) 模型拟合到数据。

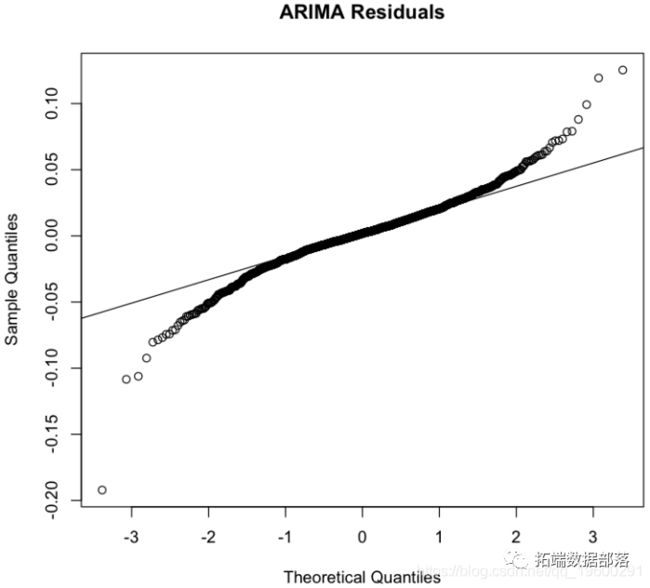
eimae(dl,r);

Est是一个完全指定的 garch 模型对象。也就是说，它不包含 NaN 值。您可以通过使用生成残差infer，然后对其进行分析来评估模型的充分性。

要模拟条件方差或序列，请传递 Est 到 simulate。

要预测分布，请 Est转到 forecast.

模拟 GARCH 模型观察序列和条件方差

从完全指定的garch 模型对象模拟条件方差或序列路径。也就是说，从估计garch 模型或已知 garch 模型（您在其中指定所有参数值）进行模拟。

加载 Data 数据集。

RN;

创建具有未知条件平均偏移量的 GARCH(1,1) 模型。将模型拟合到年度收益序列。

gach('GCHLgs',1,ARCLgs',1,Ofet',Na);
Est = esiae(Mnr);

从估计的 GARCH 模型模拟每个时期的 100 条条件方差和序列路径。

mOb = nul(n); % 样本大小（T）
nuths = 100;     % 要模拟的路径数
rg(1);             % 用于重现
[Vim,Sm] = simae(EMdl,nuOs,NumPts,umPts);

VSim 和 YSim 是 T-by- numPaths 矩阵。行对应一个采样周期，列对应一个模拟路径。

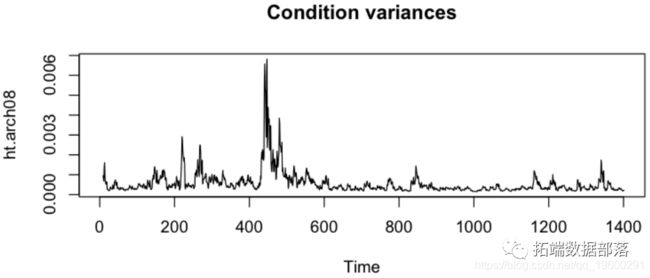
绘制模拟路径的平均值以及 97.5% 和 2.5% 的百分位数。将模拟统计数据与原始数据进行比较。

Var = men(Vim,2);
VSI = quntie(Vi,[0.025 0.975],2);
Ymar = man(YSm,2);
YCI = qatle(Sim,[0.025 0.975],2);

pot(ae,im,);
hld on;
h2 = plt(des,Viar);
h =plo(ats,VSiCI,
hld off;

预测 GARCH 模型条件方差

从完全指定的garch 模型对象预测条件方差。也就是说，根据估计garch 模型或garch 您指定所有参数值的已知模型进行预测。

加载 Data 数据集。

RN;

创建具有未知条件平均偏移量的 GARCH(1,1) 模型，并将该模型拟合到年度收益率序列。

dl = grh('GCas',1,'AHas',1,'Ofet',aN);
Edl = esate(dl,r);

使用估计的 GARCH 模型预测未来 10 年收益率序列的条件方差。将整个收益系列指定为样本前观察。软件使用样本前观测值和模型推断样本前条件方差。

numPeiods = 10;
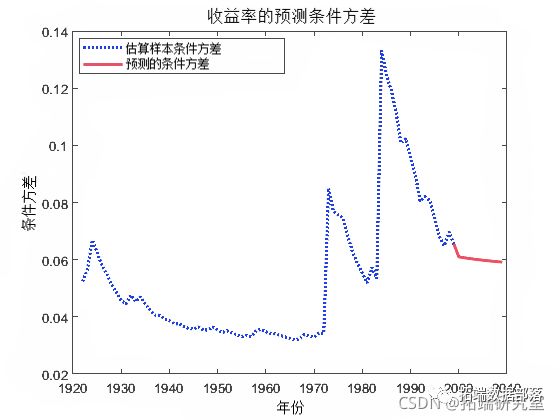
F = foeast(EtMdl,uPes,nr);

绘制名义收益的预测条件方差。将预测与观察到的条件方差进行比较。

fgure;
pot(dtes);
hld n;
pot(dts(ed):ds(ed) + 10,[v(nd);vF]);

参考

[1] Tsay，_金融时间序列的_RS _分析_。第 3 版。John Wiley & Sons, Inc.，2010 年。

点击文末 “阅读原文”

获取全文完整资料。

本文选自《MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测》。