最小生成树——prim算法实现

案例引入

N个城市之间需要铺设一张交通网，使任意两个城市间都有交通路线直达，现已知各个城市之间铺设道路的经济成本，问该如何求算铺网的最低经济成本？为求算最低经济成本，可以假设N个城市就是连通网G的N个顶点，而求算最低成本问题可以转化为在N个城市间找到N-1条边，使这些边的权值之和达到最小。在N个顶点之间可以生成许多棵不同的生成树，而最合理的交通网就是N-1条边权值之和最小的生成树。

最小生成树定义

在一个连通网的所有生成树当中，各边权值之和最小的那棵生成树就叫做连通网的最小代价树，简称最小生成树。

MST性质

在构造最小生成树中，难免脱离不了对MST性质的应用。

该性质的定义为：假设U为连通网G=（V,E）中V的非空子集合，若（u,v）是一条权值最小的边，其中,那么必定存在一棵G的最小生成树包含(u,v)。

反证法：假设G的任意一棵最小生成树都不包含（u,v），设T为G的一棵最小生成树，那么必定存在（u1,v1）为T的一条边，且 .此时若在T中加入(u,v)，那么新树newT一定存在环（在T中U集与V-U集分别可以构成两个连通分量），由于,可知u与u1在U集中是连通的，v与v1在V-U集中也是连通的，那么去掉(u1,v1)则将消除树的环，同时(u,v)可使U与V-U这两个连通分量重新组合成为一棵生成树。由于(u,v)的权值比(u1,v1)大，故(u,v)必定存在于某一棵最小树中。证明完毕！

普里姆算法

算法思路

该算法也称为“加点法”，即每次都选取一条权值最小的边（u,v）加入到最小生成树中,其中，使v加入到U中并且更新U到V-U各个顶点的最小权值边；重复上述步骤，直到V=U为止。

我们可以将U看成一棵树，该树到V-U的各个顶点的权值最小边由U中的某个顶点决定，比如求算U到v的权值最小需要逐一比较U中的已有顶点到v的距离，选取到达v的距离最小的顶点u，规定(u,v)为U到V-U中顶点v的权值最小边。

普里姆算法的构造过程

假设N=（V,E）是连通网，TE是N上最小生成树的最小边集合。

1. 初始化U={u0},TE={空}，;

2. 选取U到V-U的最小权值边(u,v)，将v加入到U中，（u,v）加入TE。由于v的加入，需要更新U到V-U的最小权值边；

3. 重复步骤（2),直到U=V，构造结束。

注意事项：假如存在两条权值相同的最小边，则任意选取一条边加入TE。

辅助数组

由于需要选取U到V-U的最小权值边，故需要借助一个辅助数组Assistarr[mvnum]记录U到V-U的各个最小权值边。其中数组下标为顶点在邻接矩阵中的下标（待会用邻接矩阵作为连通网的存储结构），adject表示U到V-U最小权值边(u,v)中的顶点u，lowcost表示边(u,v)的最小权值，其中lowcost==0表示顶点已在U中，无需再次加入。

代码实现

//文件名为:AMGraph.h
#pragma once
#include
using namespace std;

//先实现邻接矩阵的搜索算法
#define Mvnum 100  //最大顶点数
typedef char VerType;  //顶点数据类型
typedef int ArcType;  //边的数据类型
typedef struct AMGraph {
    int vexnum, arcnum;
    VerType vexs[Mvnum];  //顶点信息表
    ArcType arcs[Mvnum][Mvnum];   //邻接矩阵
}AMGraph;
//创建无向网
void CreateUDN(AMGraph& G);

//文件名：AMGraph.cpp
#include"AMGraph.h"
//用邻接矩阵创建无向网
void CreateUDN(AMGraph& G)
{
    //表示无穷大，以方便生成最小生成树
    int inf = 999999999;
    //输入顶点与边的个数，图的第一部分信息
    cin >> G.vexnum >> G.arcnum;
    //判断合法性
    if (G.vexnum > Mvnum || G.arcnum > (G.vexnum - 1) * G.vexnum / 2)
    {
        cout << "所输入信息非法" << endl;
        return;
    }
    //紧接着输入顶点的信息,图的第二部分信息
    for (int i = 0;i < G.vexnum;i++)
    {
        cin >> G.vexs[i];
    }
    //将图的边初始化,权值全部置为inf，inf表示无穷大
    for (int i = 0;i < G.vexnum;i++)
    {
        for (int j = 0;j < G.vexnum;j++)
            G.arcs[i][j] = inf;
    }
    //输入权值
    for (int i = 0;i < G.arcnum;i++)
    {
        //输入v1,v2作为边(v1,v2)的顶点以及边之间的权值w
        //编号从0开始
        int v1, v2, w;
        //此处省略了查找v1,v2编号的过程
        cin >> v1 >> v2 >> w;
        //时刻关注合法性
        if (v1 == v2 || v1 >= G.vexnum || v2 >= G.vexnum
            || v1 < 0 || v2 < 0)
        {
            i--;
            continue;
        }
        if (G.arcs[v1][v2] != inf)
        {
            i--;
            continue;
        }
        //输入边的权值
        G.arcs[v1][v2] = G.arcs[v2][v1] = w;
    }
    //创建完毕
}

//文件名：prim.h
#pragma once
#include"AMGraph.h"

//定义辅助数组
typedef struct closedge {
    //最小边(u,v)在U中的顶点
    VerType adject;
    //U到k的最小权值
    ArcType lowcost;
}closedge;

//普里姆算法声明
void MiniSpanTree_Prim(const AMGraph& G, VerType u);

//查找下标函数
int LocateVex(const AMGraph& G, VerType u);

//找权值最小边，返回其在辅助数组中的下标
//注意数组名本身就是一个常量地址，不能传引用
int Findminarc(const AMGraph& G, const closedge* Assistarr);

//文件名：prim.cpp
#include"prim.h"

//辅助数组
closedge Assistarr[Mvnum];

//查找下标函数
int LocateVex(const AMGraph& G, VerType u)
{
    for (int i = 0;i < G.vexnum;i++)
    {
        if (G.vexs[i] == u)
            return i;
    }
    //表示没有找到，一般都不会出现这种情况
    return -1;
}

//找权值最小边，返回其在辅助数组中的下标
int Findminarc(const AMGraph& G, const closedge*Assistarr)
{
    int mark = 999999999;
    int k = 0;
    for (int i = 0;i < G.vexnum;i++)
    {
        //排除已经在U中的顶点，该顶点下标为i
        if (Assistarr[i].lowcost != 0)
        {
            if (mark > Assistarr[i].lowcost)
            {
                mark = Assistarr[i].lowcost;
                k = i;
            }
        }
    }
    return k;
}

//实现普里姆算法，针对连通图而言
void MiniSpanTree_Prim(const AMGraph& G, VerType u)
{
    //查找到u的下标，更新Assistarr数组的数据
    int k = LocateVex(G, u);
    if (k == -1)
    {
        cout << "顶点不存在" << endl;
        return;
    }
    //更新Assistarr数组
    for (int i = 0;i < G.vexnum;i++)
    {
        if (i != k)
        {
            //最小边(u0,v0)在U上的顶点最初都为u
            Assistarr[i].adject = u;
            //最小边的权值最初都为(u,v0)
            Assistarr[i].lowcost = G.arcs[k][i];
        }
    }
    //规定，如果Assistarr[i].lowcost ==0，则表示下标为i的顶点
    //已经在U中
    //顶点u一开始就在数组中，故Assistarr[k].lowest = 0;
    Assistarr[k].lowcost = 0;
    //紧接着，将剩余的n-1个顶点加入到U中
    for (int i = 1;i < G.vexnum;i++)
    {
        //找到权值最小边(u,v),u在U中，v在V-U中，因此只需要放回最小边在
        //数组中的下标k
        int k = Findminarc(G,Assistarr);
        //在U中的顶点
        VerType u0 = Assistarr[k].adject;
        //通过下标k在vexs数组中找到其顶点值
        VerType v0 = G.vexs[k];
        //打印最小生成树的一条边
        cout << u0 << "--" << v0 << endl;
        //将下标为k的顶点加入到U中
        Assistarr[k].lowcost = 0;
        //更新最小权值边
        for (int j = 0;j < G.vexnum;j++)
        {
            //G.arcs[k][j]表示(k,j)的权值，Assistarr[j].lowcost
            //表示目前U中的顶点到V-U下标为j的最小权值
            if (G.arcs[k][j] < Assistarr[j].lowcost)
            {
                Assistarr[j].lowcost = G.arcs[k][j];
                Assistarr[j].adject = G.vexs[k];
            }
        }
    }
}

测试

void test01()
{
    AMGraph G;
    CreateUDN(G);
    MiniSpanTree_Prim(G, G.vexs[0]);
}

int main()
{
    test01();
    return 0;
}

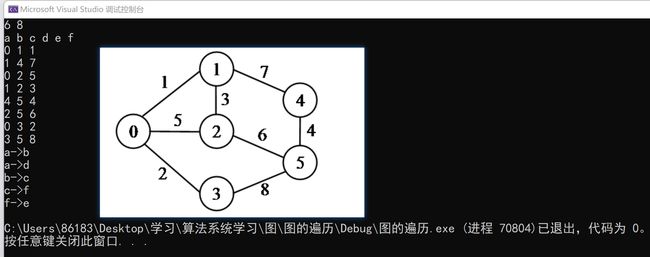
测试结果

算法分析

在上述算法的二层循环中，第一层循环旨在将n-1条边加入到TE，故需要循环n-1次。同时，每次找最小权值边与更新最小权值边都需要扫描n次，因此时间复杂度为O(n^2)。算法的时间复杂度与顶点的个数有关，与图的存储结构无关，因此prim算法适合于稠密图。另外，由于辅助数组也会产生额外的内存空间，故空间复杂度为O(n)。