AcWing 843. n-皇后问题

题目描述

---

分析：

n 皇后问题即是深搜(DFS)问题，与之前的排列数字相同，是在一定的约束条件下进行的，只是n 皇后要求的约束条件复杂一些：即任意两个皇后都不能处于同一行、同一列或同一斜线上。关键点在于如何记录和判断约束条件，排列数字中使用 $used[]$ 数组来记录每个数字的使用情况。那么如何判断两个皇后是否在同一行、同一列、同一斜线上呢？这是解题的关键，我们依然使用数组。具体为 $row[],col[],dia[],udia[]$。

if (!row[x] && !col[y] && !dia[x - y + n] && !udia[x + y])

此代码为是否放皇后的判断语句。row[x]和col[y]的意思很明显，如果为空，即代表之前没有皇后下在了相同的x或y的行列上，本次就可以下皇后。不好理解的点是dia[x - y + n]以及udia[x + y]。请看下面的分析：

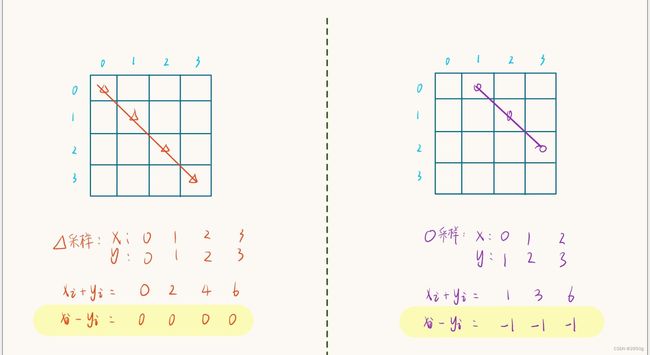
对于判断是否在同一主斜线（棋盘内与主对角线平行的斜线），我们使用 dia[] 数组，可以任取一个棋盘位(x,y)，并观察主斜线上该点与其他点位之前的规律：

可以发现：主斜线上采样的多个点的x、y值的差，即说明多个点可通过减法映射到数组中的同一位置，判断斜线上是否出现过一次皇后，即查看 dia[x - y] 是否为空即可。但这样做减法时会得到一个负数，是没法直接映射到数组中的，因此主斜线上做判断时统一加上一个常量保证非负，即dia[x - y + n]。

同理，对于判断是否在同一副斜线（棋盘内与副对角线平行的斜线），我们使用 udia[] 数组，可以任取一个棋盘位(x,y)，并观察副斜线上该点与其他点位之前的规律：

可以发现：主斜线上采样的多个点的x、y值的和，即说明多个点可通过加法映射到数组中的同一位置，判断斜线上是否出现过一次皇后，即判断 udia[x + y] 是否为空即可。

---

代码：

// 该搜索顺序是按照棋盘上格子的顺序，自上而下，自左而右
#include 

using namespace std;


const int N = 10;

int n;
// 在这里 dia 为主斜线，udia 为副斜线方向
// 对角线个数是 2n - 1，因此数组大小开到 N * 2
int row[N], col[N], dia[N * 2], udia[N * 2];
char g[N][N];


void dfs(int x, int y, int s)
{
    // 查询的位置出了棋盘的当前行，强行放到下一行
    if (y == n) y = 0, x ++;
    
    if (x == n)
    {
        // 来到了最后一行，并且皇后已经全部放完，即找到了一组解
        if (s == n)
        {
            // 按行输出棋盘情况
            for (int i = 0; i < n; i ++) puts(g[i]);
            puts("");
        }
        return ;
    }
    
    
    //当前格子放皇后
    if (!row[x] && !col[y] && !dia[x - y + n] && !udia[x + y])
    {
        g[x][y] = 'Q';
        row[x] = col[y] = dia[x - y + n] = udia[x + y] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dia[x - y + n] = udia[x + y] = false;
        g[x][y] = '.';
    }
    
    // 当前格子不放皇后
    dfs(x, y + 1, s);
}


int main()
{
    cin >> n;
    
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n; j ++)
            g[i][j] = '.';
            
    // 三个参数分别是开始搜索的行、列以及当前放下了多少个皇后
    // 即从左上角开始搜索
    dfs(0, 0, 0);
    
    return 0;
}

代码(Python3)：

def dfs(x, y, s):
    if y == n:
        x += 1
        y = 0
    if x == n:
        if s == n:
            for i in range(n):
                print(''. join(g[i]))
            print()
        return
    
    if not row[x] and not col[y] and not dia[x - y + n] and not udia[x + y]:
        g[x][y] = 'Q'
        row[x] = col[y] = dia[x - y + n] = udia[x + y] = True
        dfs(x, y + 1, s + 1)
        g[x][y] = '.'
        row[x] = col[y] = dia[x - y + n] = udia[x + y] = False
    
    dfs(x, y + 1, s)
            

if __name__ == "__main__":
    
    N = 10
    n = int(input())
    row = [0] * N
    col = [0] * N
    dia = [0] * (N * 2)
    udia = [0] * (N * 2)
    g = [['.' for i in range(n)] for i in range(n)]
    
    dfs(0, 0, 0)

---