数据结构-考研难点代码突破（C++实现有向图最短路径算法（Dijkstra，Floyd-Warshall算法）图解操作细节（引自C语言中文网））

以代码的方式复习考研数据结构知识点，这里在考研不以代码为重点，而是以实现过程为重点

1. 最短路径

图的生成树针对的是无向图，图的最短路径一般是针对的是有向图。

之前介绍的利用广度优先搜索查找最短路径只是对无权图而言的

当图是带权图时，把从一个顶点a到图中其余任意一个顶点x的一条路径（可能不止一条）所经过边上的权值之和，定义为该路径的带权路径长度，把带权路径长度最短的那条路径称为最短路径.

求解最短路径的算法通常都依赖于一种性质，即两点之间的最短路径也包含了路径上其他顶点间的最短路径。

带权有向图G的最短路径问题一般可分为两类∶

1. 是单源最短路径，即求图中某一顶点到其他各顶点的最短路径，可通过经典的 Dijkstra（迪杰斯特拉），Bellman-Ford（）算法求解
2. 是多源最短路径，即求每对顶点间的最短路径，可通过Floyd（弗洛伊德）算法来求解

2. 单源最短路径

单源最短路径问题：给定一个有向图G = < V ， E > ，求源结点s ∈ V到图中每个结点v ∈ V 的最短路径给一个点A，A点到图的其他点的最短路径。

ⅠDijkstra算法

Dijkstra算法适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点 和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。

如果出现权值为负数的单源最短路径问题，只能使用Bellman-Ford算法。

算法思路：C语言中文网
eg：

如上图，假设需要统计顶点0到其他顶点的最短路径

如果两个顶点之间无法直达，对应的权值为无穷大，用∞ 表示

1. 统计从顶点 0 直达其它顶点的权值
   
2. 表 1 中，权值最小的是 0-1 路径，它也是从顶点 0 到顶点 1 的最短路径（如图 2 所示）。原因很简单，从顶点 0 出发一共只有 0-1 和 0-2 两条路径，0-2 的权值本就比 0-1 大，所以从 0-2 出发不可能找得到比 0-1 权值更小的路径
   
3. 找到最短路径 0-1 后，沿 0-1 路径方向查找更短的到达其它顶点的路径，并对表 1 进行更新。
   
   更新后的表格如表 2 所示，沿 0-1 路径可以到达顶点 3，且 0-1-3 的总权值比 0-3 更小。表 2 中，总权值最小的路径是 0-2，它也是从顶点 0 到顶点 2 的最短路径，如下图所示
   
4. 重复之前的操作，沿 0-2 路径方向查找更短的到达其它顶点的路径。遗憾地是，从顶点 2 只能到达顶点 3，且 0-2-3 的总权值比表 2 中记录的 0-1-3 更大，因此表 2 中记录的数据维持不变。
   
   总权值最小的是 0-1-3，它也是顶点 0 到顶点 3 的最短路径。
   
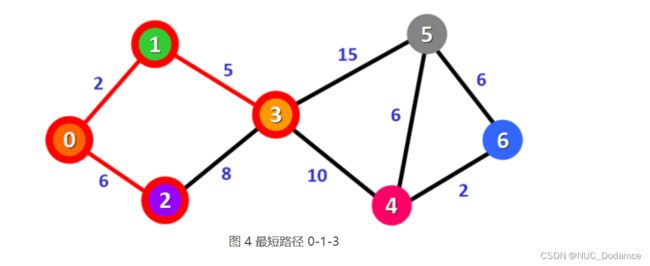
   沿 0-1-3 路径方向，查找到其它顶点更短的路径并更新表 3。更新后的表格为：
   
5. 表 4 中，总权值最小的是 0-1-3-4，它是顶点 0 到顶点 4 的最短路径。
   
   从顶点 4 出发，查找顶点 0 到其它顶点更短的路径并更新表 4。更新后的表格为：
   
6. 表 5 中，总权值最小的路径是 0-1-3-4-6，它是顶点 0 到顶点 6 的最短路径。
   
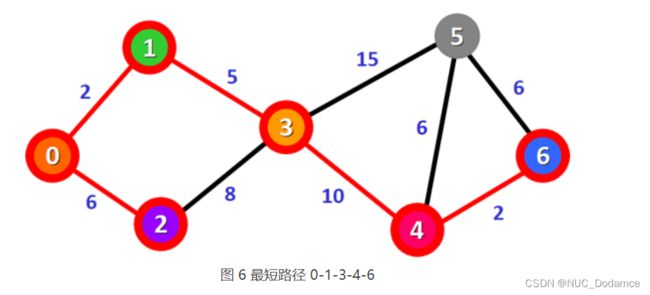
7. 从图 6 可以看到，只剩下顶点 0 到顶点 5 的最短路径尚未确定。从顶点 6 出发到达顶点 5 的路径是 0-1-3-4-6-5，对应的总权值为 25，大于表 5 中记录的 0-1-3-5 路径，因此 0-1-3-5 是顶点 0 到顶点 5 的最短路径。
   

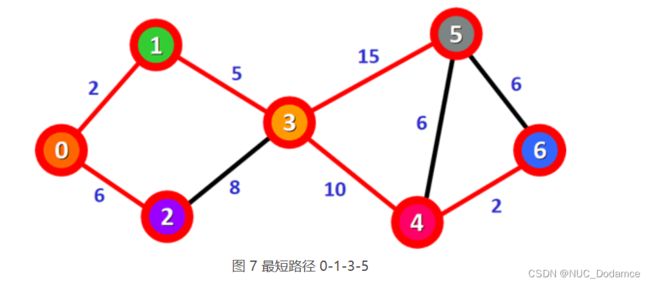
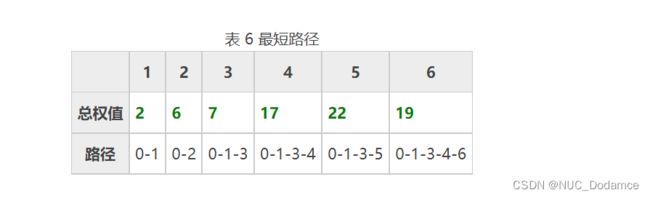
最终，通过Dijkstra算法计算出0到图其他节点的最短路径为：

C++代码

这里使用邻接矩阵保存边关系

顶点保存在dist数组中，数组下标代表顶点编号，数组下标值代表源顶点到这个顶点的最短路径长度。初始化默认值（无穷）

为了保存最短路径之间的节点，这里使用数组pPath的形式保存每一个顶点的父节点。（存储的是路径中所有顶点最短路径的前一个顶点下标）数组初始化为-1。
类似并查集找根节点的过程

Dijkstra算法

// 邻接矩阵法存储图结构

#include 
#include 
#include 
#include 
#include 
#include 

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }

    //-------------------------------Dijkstra---------------------------
    /**
     * @brief 单源最短路径
     *
     * @param src 起点
     * @param dist dist保存src到各个顶点的最短距离
     * @param pPath pPath:保存最短路径的节点对应下标
     */
    void Dijkstra(const v &src, std::vector<w> &dist, std::vector<int> &pPath)
    {
        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        pPath.resize(size, -1);
        dist.resize(size, max);

        dist[pos] = 0;    // 源顶点到自己本身最短距离为0
        pPath[pos] = pos; // 源顶点的最短路径的父节点是自己本身

        std::vector<bool> S(size, false); // 已经确定最短路径的顶点的集合

        for (size_t time = 0; time < size; time++)
        {
            // 选不在S集合 最短路径的顶点，更新其他路径
            int p = 0;
            w min = max;

            for (size_t i = 0; i < size; i++)
            {
                if (S[i] == false && dist[i] < min)
                {
                    p = i;
                    min = dist[i];
                }
            }

            // 把p放到S集合中
            S[p] = true;

            // src->p + p->p邻接节点 与 src ->p邻接节点权值相比较小，要更新
            for (size_t adP = 0; adP < size; adP++)
            {
                // 找到p点邻接顶点
                if (S[adP] == false && _matrix[p][adP] != max)
                {
                    if ((dist[p] + _matrix[p][adP]) < dist[adP])
                    {
                        dist[adP] = dist[p] + _matrix[p][adP];

                        // 更新最短路径父节点
                        pPath[adP] = p;
                    }
                }
            }
        }
    }

    /**
     * @brief 单源最短路径
     *
     * @param src 起点
     * @param dist dist保存src到各个顶点的最短距离
     */
    void Dijkstra(const v &src, std::vector<w> &dist)
    {
        std::vector<int> pPath;
        Dijkstra(src, dist, pPath);

        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        for (size_t i = 0; i < size; i++)
        {
            if (i != pos)
            {
                std::vector<int> path;
                size_t dst_pos = i;
                std::cout << "最短路径为:";
                while (dst_pos != pos)
                {
                    path.push_back(dst_pos);
                    dst_pos = pPath[dst_pos];
                }
                path.push_back(pos);
                std::reverse(path.begin(), path.end());
                for (size_t j = 0; j < path.size(); j++)
                {
                    std::cout << _verPoint[path[j]];
                    if (j != path.size() - 1)
                    {
                        std::cout << "->";
                    }
                }
                std::cout << "长度: " << dist[i] << std::endl;
            }
        }
    }
};

#include "Dijkstra.h"

using namespace std;

int main(int argc, char const *argv[])
{
    graph<char, int> g({'0', '1', '2', '3', '4', '5', '6'});
    g.AddEdge('0', '1', 2);
    g.AddEdge('0', '2', 6);
    g.AddEdge('1', '3', 5);
    g.AddEdge('2', '3', 8);
    g.AddEdge('3', '5', 15);
    g.AddEdge('3', '4', 10);
    g.AddEdge('4', '5', 6);
    g.AddEdge('4', '6', 2);
    g.AddEdge('6', '5', 6);
    g.PrintGraph();

    vector<int> dist;
    g.Dijkstra('0', dist);

    return 0;
}

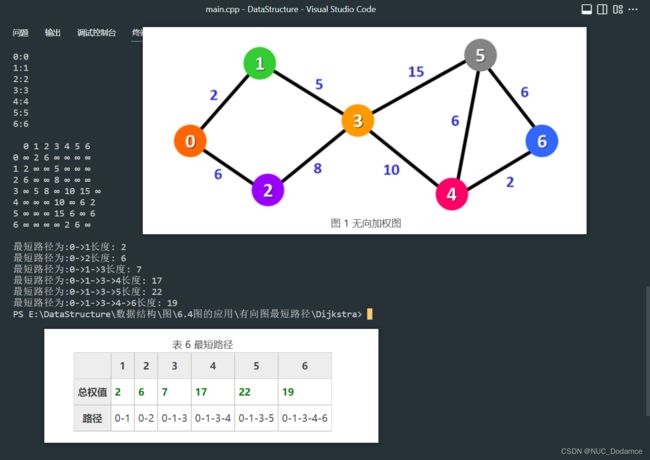
算法的时间复杂度为O(N²)，空间复杂度O(N)（N为顶点个数）

此外Dijkstra算法不适用于带负值的权值，使用于带负权的有向图最短路径算法为Bellman-Ford算法

3. 多源最短路径

多源最短路径：源顶点是图中的所有顶点，求图中任意两点的最短路径。

Ⅰ Floyd-Warshall算法

注意：

1. Floyd-Warshall可以解决负数权值问题。
2. 如果以所有点为源点，使用Dijkstra算法也可以算出图中任意两点的最短路径。但是Dijkstra算法不能带负数权值，Bellman-Ford算法效率太低。

Floyd-Warshall算法：
因为Floyd-Warshall算法要以图中任意顶点为源顶点。
根据上面分析可知，dist（记录源顶点到其他顶点的最短路径）数组应该是二维数组。
pPath（通过双亲表示法记录最短路径的节点）也应该是二维数组。

算法的思路是通过动态规划得出的。
eg：

1. 建立一张表格，记录每个顶点直达其它所有顶点的权值：
   

2. 在表 1 的基础上，将顶点 1 作为 “中间顶点”，计算从各个顶点出发途径顶点 1 再到达其它顶点的权值，如果比表 1 中记录的权值更小，证明两个顶点之间存在更短的路径，对表 1 进行更新。

   从各个顶点出发，途径顶点 1 再到达其它顶点的路径以及对应的权值分别是：
   2-1-3：权值为 2 + ∞ = ∞，表 1 中记录的 2-3 的权值也是 ∞；
   2-1-4：权值为 2 + 5 = 7，表 1 中记录的 2-4 的权值是 4；
   3-1-2：权值为 ∞ + 3，表 1 中记录的 3-2 的权值是 1；
   3-1-4：权值为 ∞ + 5，表 1 中记录的 3-4 的权值是 ∞；
   4-1-2：权值为 ∞ + 3，表 1 中记录的 4-2 的权值是 ∞；
   4-1-3：权值为 ∞ + ∞，表 1 中记录的 4-3 的权值是 2。

   以上所有的路径中，没有比表 1 中记录的权值最小的路径，所以不需要对表 1 进行更新。

3. 在表 1 的基础上，以顶点 2 作为 “中间顶点”，计算从各个顶点出发途径顶点 2 再到达其它顶点的权值：

   1-2-3：权值为 3 + ∞，表 1 中记录的 1-3 的权值为 ∞；
   1-2-4：权值为 3 + 4 = 7，表 1 中 1-4 的权值为 5；
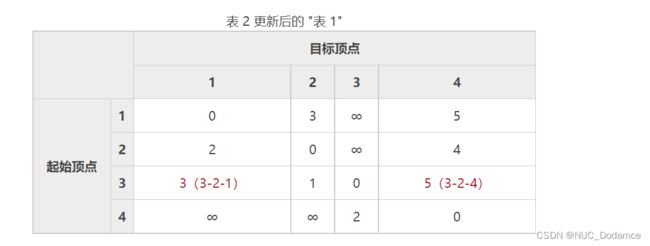
   3-2-1：权值为 1 + 2 = 3，表 1 中 3-1 的权值为 ∞，3 < ∞；
   3-2-4：权值为 1 + 4 = 5，表 1 中 3-4 的权值为 ∞，5 < ∞；
   4-2-1：权值为 ∞ + 2，表 1 中 4-1 的权值为 ∞；
   4-2-3：权值为 ∞ + ∞，表 1 中 4-3 的权值为 2。

   以顶点 2 作为 “中间顶点”，我们找到了比 3-1、3-4 更短的路径，对表 1 进行更新：
   

4. 以此类推，分别以不同顶点为中间顶点，不断更新表，最终更新结果为

C++代码

时间复杂度：O(N³)，空间复杂度O(N)

// 邻接矩阵法存储图结构

#include 
#include 
#include 
#include 
#include 
#include 

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }

    //-------------------------------Floyd-Warshall---------------------------
    /**
     * @brief 多源最短路径
     *
     * @param vDist （记录源顶点到其他顶点的最短路径）数组应该是二维数组。
     * @param vPath （通过双亲表示法记录最短路径的节点）也应该是二维数组。
     */
    void FloydWarShall(std::vector<std::vector<w>> &vDist, std::vector<std::vector<int>> &vPath)
    {
        size_t size = _verPoint.size();

        // 初始化顶点距离矩阵和路径矩阵
        vDist.resize(size);
        vPath.resize(size);
        for (size_t i = 0; i < size; i++)
        {
            vDist[i].resize(size, max);
            vPath[i].resize(size, -1);
        }

        // 直接相连的边更新初始化

        for (size_t i = 0; i < size; i++)
        {
            for (size_t j = 0; j < size; j++)
            {
                if (_matrix[i][j] != max)
                {
                    vDist[i][j] = _matrix[i][j];
                    vPath[i][j] = i; // i->j起点是i点
                }
                if (i == j)
                {
                    vDist[i][j] = w();
                }
            }
        }

        // 最短路径的更新i->{其他顶点}->j
        // k作为中间点，尝试更新i->j的路径
        for (size_t k = 0; k < size; k++)
        {
            for (size_t i = 0; i < size; i++)
            {
                for (size_t j = 0; j < size; j++)
                {
                    if (vDist[i][k] != max && vDist[k][j] != max)
                    {
                        if (vDist[i][k] + vDist[k][j] < vDist[i][j])
                        {
                            // 经过k点更短，更新长度
                            vDist[i][j] = vDist[i][k] + vDist[k][j];
                            // 修改父亲节点
                            // 找上一个与j邻接的节点
                            // k->j 如果k与j直接相连，则vPath[i][j]=k
                            // 但是k->j不一定直接相连 k->...->x->j则vPath[i][j]=x,就是vPath[k][j]
                            vPath[i][j] = vPath[k][j];
                        }
                    }
                }
            }
        }
    }

    void _PrintShortLine(const v &src, std::vector<w> &dist, std::vector<int> pPath)
    {
        size_t pos = _getPosPoint(src);
        size_t size = _verPoint.size();
        for (size_t i = 0; i < size; i++)
        {
            if (i != pos)
            {
                std::vector<int> path;
                size_t dst_pos = i;
                std::cout << "最短路径为:";
                while (dst_pos != pos)
                {
                    path.push_back(dst_pos);
                    dst_pos = pPath[dst_pos];
                }
                path.push_back(pos);
                std::reverse(path.begin(), path.end());
                for (size_t j = 0; j < path.size(); j++)
                {
                    std::cout << _verPoint[path[j]];
                    if (j != path.size() - 1)
                    {
                        std::cout << "->";
                    }
                }
                std::cout << "长度: " << dist[i] << std::endl;
            }
        }
    }

    void PrintFloyd(std::vector<std::vector<w>> &vDist, std::vector<std::vector<int>> &vPath)
    {
        FloydWarShall(vDist, vPath);

        for (int i = 0; i < _verPoint.size(); i++)
        {
            _PrintShortLine(_verPoint[i], vDist[i], vPath[i]);
            std::cout << "\n";
        }
    }
};

#include "Floyd-Warshall.h"

using namespace std;

int main(int argc, char const *argv[])
{
    graph<char, int, INT_MAX, true> g({'1', '2', '3', '4'});
    g.AddEdge('1', '2', 3);
    g.AddEdge('1', '4', 5);
    g.AddEdge('2', '1', 2);
    g.AddEdge('4', '3', 2);
    g.AddEdge('2', '4', 4);
    g.AddEdge('3', '2', 1);
    g.PrintGraph();

    vector<vector<int>> vDist;
    vector<vector<int>> vPath;
    g.FloydWarShall(vDist, vPath);
    g.PrintFloyd(vDist, vPath);
    return 0;
}