使用QIS(Quantum Image Sensor)图像重建总结(1)
最近看了不少使用QIS重建图像的文章,觉得比较完整详细的还是Abhiram Gnanasambandam的博士论文:https://hammer.purdue.edu/articles/thesis/Computer_vision_at_low_light/20057081
1 介绍
讲述了又墨子的小孔成像原理,到交卷相机,再到数字相机的发展过程。指出本文的主要目的是为了针对光子随机到达相机产生的散粒噪声(即使是完美的传感器也没有办法避免),提出相应的解决思路。

作者指出现有的相机在照度超过25lux的场景下都能取得较好的重建效果,而当照度只有2.5lux时,通过高增益(或者ISO)可以从传感器中获得有价值的信号。而当照度到0.25lux及以下的时候,即使使用了高增益,图片的质量也会很差。
如下图所示,即使是使用完美的传感器(传感器自身不带噪声),低光照情况下仍然有很严重的散粒噪声。
同时,低光照也会对颜色重建产生影响,相机通常使用CFA(Color Filter Arrays)来进行图像颜色的构建,从CFA中的单一图像通道恢复三通道RGB图像的过程也叫作去马赛克。低光照会使得这一过程更加困难(主要还是噪声的影响)。
低光照同样会对目标检测、目标分类等下游视觉任务产生不利的影响。

针对动态场景,在低光照情况下,为了减少运动模糊,可以提高相机的帧数,但是,减少的曝光时间会导致光照不足,致使噪声增大,降低图像的SNR。

同时曝光时间较短容易造成暗处物体噪声过大,曝光时间较长又容易造成亮出物体过曝。如何保证相机的HDR(High Dynamic Range),即如何在一张图形中使得受光照强度不同的物体都展现出良好的拍摄效果,也是一个很重要的问题。

所以本文希望借助QIS传感器(拥有更小的读出噪声、暗电流以及像素块),在低光照、HDR场景下获得成像良好的图像。
2 数字图像传感器
2.1 现代相机的历史
现代相机的发展可以从卤化银薄膜技术说起,其主要原理是卤化银和光的反应,光子会打破卤化银中的化学键,从而产生银,而光子的数量决定了银的产生数量,通过这样的方式和后续处理,就得到了最终的图像。在卤化银相机中,胶卷同时作为图像捕捉和保存的媒介。
而随后的电子相机,则将图像捕捉和存储的任务给分开了,通过图像传感器捕捉场景,然后将其存储在格外的空间中。
最早的数码相机是基于CCD(Charge-Coupled Device)技术的,CCD传感器通过测量电荷,再经过ADC(Analog-to-Digital Conversion)得到最终的数字量。而后CMOS传感器开始兴起,其主可以在像素内实现成像以及ADC。期初,CCD靠着自己低读出噪声、暗电流,高量子转化效率的优势在相机产业占据优势,但随着科技的发展,特别是CIS(CMOS Image Sensor)像素制造技术的进步,CIS凭借自身功耗小,处理速度快的优势,以及处理噪声的降低,逐渐成为了相机产业的主导传感器。
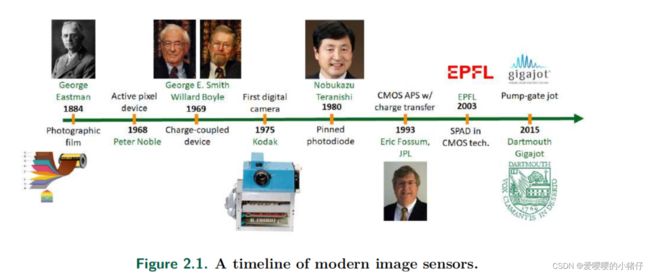
随着人们对高像素、低功耗的需求,图像的像素尺寸在持续下降,然后小的像素尺寸会造成满阱容量,即每个像素点可以收集的最大电子数量的下降,进一步导致SNR的下降。在这种情况下,Dr. Eric Fossum提出了QIS,这是一种新型的传感器,只有亚衍射极限大小的像素,并且它的满阱容量只有一,即只能收集到一个电子,它拥有对每一个光子进行计数,每秒钟几千次成像的能力。
另一种QIS的替代技术是SPAD(Single-Photon Avalanche diode),SPAD通过雪崩倍增的方式实现单光子计数。
2.2 半导体基础
2.2.1 反向偏置p-n结
p结包含了大量的可移动的正电荷(空穴),n结则包含了大量的可移动的负电荷。当p结和n结摆放在一起时,就会构成耗散区,其中包含了正负离子。p结中的大量可移动正电荷会向n结扩散,n结中的大量可移动的电子则会向p结扩散,然后构成和扩散运动相反的内电场,当内电场阻碍和扩散运动达成平衡时,就会形成稳定的耗散区。可以通过增加反向电压(p结接低电压,n结接高电压)的方式增大耗散区(此时,耗散区外的载流子会验证外电场的方向移动,耗散区增大)。同理,如果增加正向电压(p结接高电压,n结接低电压),则耗散区会变小。

2.2.2 光电效应和光电二极管
光电效应主要指当光波照射到材料上时,光子会把自身的能量转换到材料的电子中,使其成为自由电子。
一个光子中包含的能量主要取决于它的频率(或者波长),假设光子的频率为 v v v,则其波长为 λ \lambda λ为 λ = c v \lambda=\frac{c}{v} λ=vc( c c c为真空环境下的光速),其携带的能量为:
E = h v = h c v E=hv=\frac{hc}{v} E=hv=vhc
一个光子需要有足够的能量将电子从价电子带(受原子束缚)激活到传导带(不受原子束缚),才能产生光电效应。一个光子最多可以激活一个电子,而光子却不一定能激活电子。这种激活成功率通常称为QE(Quantum Efficiency)。

光电二极管正是使用了光电效应,光电二极管是在反向电压下工作的,无光照时呈现截止状态(只有微弱的暗电流),当有光照时,光电效应激发了大量可以自由移动的电子,由于反向电压的作用,产生较大的反向电流,光电二极管导通。一般来说反向电压越大,满阱容量也会越大。
2.3 CCD
2.3.1 MOS 电容
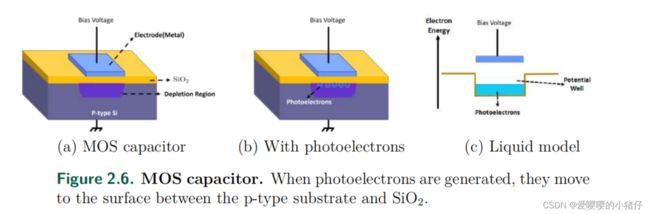
CCD传感器的基础是MOS电容。MOS电容有一个半导体基板,一个绝缘体还有一个称为栅极的金属电极。这里绝缘体相当于电容里的电介质。金属起到的作用相当于p-n结中的n结,而半导体的基板相当于p结。通过在栅极上施加电压(类似于向p-n结上施加反向电压(n结上加正向电压)),会形成一个耗散区(下图(a))。当基板里的电子被激活时,电子会涌向栅极,但是中间的绝缘层会阻隔电子,使其在绝缘层和基板之间的接触面聚集(下图(b))。也可以用一个液体模型来表示这个过程(下图©)。
2.3.2 电荷转换
下面来介绍将两块MOS电容放在一起时会发生什么情况。考虑如下图所示的情况,两个gate都正极相连,现在假设它们其中的一个积累了光生电子,一个没有,当两个距离较远时,会保持原样,当两个距离较近时,如下图(b)所示,这两个potential well会合并成一个。

当有偏向电压被施加时,会产生potential well;当电压撤去后,potential well会消失,当两个potential well距离靠近时,会完成两个potential well的合并,MOS电容间的电荷主要便是通过这种方式进行转移。

下面介绍对于一个大型传感器,如何做到这一点,主要是通过顺序的行、列读取完成。首先会将电荷一列右移,最右侧的一列电荷就会被移入read register。而read register下面会有一个floating diffusion(FD),可以将电荷转化为一个数字。然后一行一行地将read register里的电荷送入到FD中,读取数据。当read register中每一行的数据都被读出后,再将电荷整体右移一列,重复之前的步骤,直到全部电荷被读出。

2.3.3 新传感器技术的需求
从上述的电荷转移机制,我们可以发现CCD将电荷存储和电荷转移分开了。CCD的主要优势如下:
1、CCD图像传感器是优化后的光电探测器。它们不服务于其他目的,这意味着它们有很好的QE和小的暗电流。
2、引入的噪声是很小的,因为转换过程几乎是完美的。
3、考虑到只有一个floating diffusion和一个放大器,像素之间不存在不执行的问题。
当时,CCD传感器也有其缺点:
1、CCD需要比较高的电压,通常10-15V。
2、一个电荷一个电荷轮流读出的机制使其处理速度较慢。
3、由于像素块针对光子探测器进行了优化,也没有其他电路结构,在像素块内添加其他功能会变得非常困难。
2.4 CMOS图像传感器
CMOS(Complementary Metal Oxide Semiconductor)技术起源于结合了PPD(Pinned Photodiode)和像素内电荷转换的传感器。CMOS的主要优点包括:
1、CMOS APS有像素读出电路,这意味其电荷可以在像素内得到放大和ADC。像素内读出电路与X-Y寻址相结合,使CMOS图像传感器在封装像素和跳过像素这方面有极大的灵活性,这使得CMOS的处理速度很快。
2、CMOS的能耗更低,CMOS通常运行在3V左右。
3、CMOS的像素电路是高度编程话的,使CMOS APS可以很灵活地针对特征需要进行修改。
2.4.1 Pinned photodiodes
pinned phtotdiodes是现代CMOS APS的重要组成部分。下图展示了一个简化版的PPD已经它是如何进行电荷转移的。

FD使用的n+型半导体掺杂的电子密度更高,这使得FD相比PPD会产生一个更大的势阱。
在PPD顶端植入的p+增加了向FD转换电荷的效率。PPD设计的一个优势是能够进行真正的CDS(Correlated Double Sampling),在CDS中,我们两次读出FD的电压,一次是在TG关闭的时候,一次是在电荷转移后。电位的变化被读出作为像素的信号。这样,读出信号的质量得到了提高。
2.4.2 CMOS APS
下图展示了四个晶体管有源像素器的系统框架图,包括了:Transfer gate(TG),Reset(RST),Source follower(SF)和Row select(SEL)。
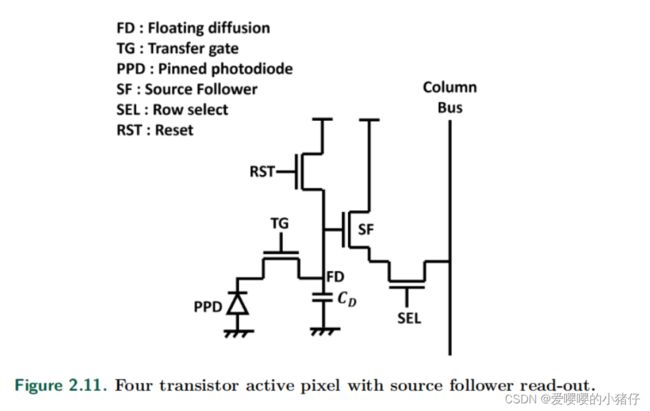
一旦TG打开,光电二极管中产生的光生电子就会被转移到FD中。FD中的电压变化 Δ V F D \Delta V_{FD} ΔVFD由FD节点的电容 C D C_D CD以及从PPD转移到转移到FD的电荷 Q P h Q_{Ph} QPh决定。
Δ V F D = Q P h C D \Delta V_{FD}=\frac{Q_{Ph}}{C_D} ΔVFD=CDQPh
从而我们可以计算出转移的电荷数 Q P h / q e Q_{Ph}/q_e QPh/qe,这里 q e q_e qe是一个电荷所带的电荷数。从而,增益(CG)可以表示为:
C G = Δ V F D Q P h / q e = q e C D CG=\frac{\Delta V_{FD}}{Q_{Ph}/q_e}=\frac{q_e}{C_D} CG=QPh/qeΔVFD=CDqe
对于一个通常的CMOS APS,CG一般是在 50 μ V / e − 1 50\mu V/e^{-1} 50μV/e−1到 100 μ V / e − 1 100\mu V/e^{-1} 100μV/e−1之间。由于噪声的影响,输出电压会有一个电子的变化。一旦电荷被转移到FD,打开SF就可以从FD中读到放大后的电压信号。接着,可以使用列总线和SEL信号选择想要从那个像素读取信号。最后,将ISO输出的电压送入到ADC中进行模数转换。
注:这里计算的增益是内在的像素增益。总体的增益是总体的放大,包含了ISO放大。
APS中的光电二极管只需要产生光生电子。像素会有一套单独的结构来进行信号放大。
尽管CMOS图像传感器拥有处理速度更快的优势,因为每一个像素都有自己独有的处理电路,但是它容易受到不一致性的影响,比如光子相应不一致性和暗电流不一致性。但是由于电路占用了一部分像素面积,导致填充因子(光敏面积与总面积的比例)降低,从而影响了灵敏度。然而,这个问题可以通过一些技术来缓解,比如背照式照明(back-side illumination,BSI)和微透镜的使用。下表展示了CCD和CMOS图像传感器在一些重要因素上的比较。

2.5 单光子计数图像传感器
CMOS在处理有限光子成像上还存在很多问题。我们想要它们具备光子计数的能力,这需要他们对每一个光子都敏感,并且可以从这些光子中获得尽可能多的信息。现在为了实现这个目标的三种方案:
1、CIS-QIS
2、SPAD
3、EMCCD(Electron multipying CCD)
通常,SPAD和CIS-QIS都可以归类到QIS中。
2.5.1 CIS-QIS
泵门点(pump-gate jot)
泵门点CIS-QIS的基础结构。由于CIS的增益取决于FD的电容 C D C_D CD。而像素内的CG需要超过1000 μ V / e − 1 \mu V/e^{-1} μV/e−1,从而取得低于 0.15 e − 1 0.15e^{-1} 0.15e−1的读出噪声。
为了减少FD的电容,可以增加TG和FD之间的距离。但是这会增加电荷转移的难度。所以提出了一种"pump"的模式。这种模式下的电荷转移过程如下图所示。

QIS
图像传感器可以使用泵门点来使得噪声到达 0.19 e − 1 0.19e^{-1} 0.19e−1。现有的CIS-QIS可以在单比特和多比特的模式上运行。可以通过减少ADC中的比特位数来得到一个高速的QIS。但比特位数和速度的取舍一直没有明确的定论。
CIS-QIS拥有CIS几乎所有的特性,所以它们拥有许多共同点:比如编程上的灵活性。CIS-QIS可以利用CIS的优势,比如BIS,CDS和微棱镜来获得良好的读出噪声,填充因子,QE和暗电流。
2.5.2 SPAD
SPAD的模型如下图所示

SPAD是专门用于反向偏压电压远高于击穿电压的传感器,这会导致一个自由的电荷就可以引起雪崩,从而产生大量的电流。CIS-QIS可以长时间地对光子计数,SPAD则不能。一旦电荷被检测到,我们需要在下次使用传感器之前重置传感器。这种现象导致了运行SPAD时存在一个死时区,传感器需要关闭从而重置像素。
SPAD需要一个高电压(15-20V)用来击穿,并且由于雪崩效用,功耗也会很高,并且SPAD的像素尺寸也会比CIS-QIS大。然而,SPAD可以达到每秒100k帧。因为高速,并且可以准确计算出雪崩发生的时间,SPAD更适合用来处理时间相关图像处理。
2.5.3 EMCCD
EMCCD本质上还是CCD,它在移位寄存机和ADC之间配备了多个增益寄存器。每个增益寄存器都会尝试使用冲击电离来进行电子倍增。冲击电离和雪崩二极管的操作非常类似,通过一个高电场加速电荷,希望引起雪崩效应。但是,EMCCD中一个光子倍增的概率非常低。EMCCD通过拥有多个这样的寄存器来获得合适的电子检测概率。和SPAD和CIS-QIS相比,EMCCD拥有一个非常高的暗电流,并且必须在低温下运行。
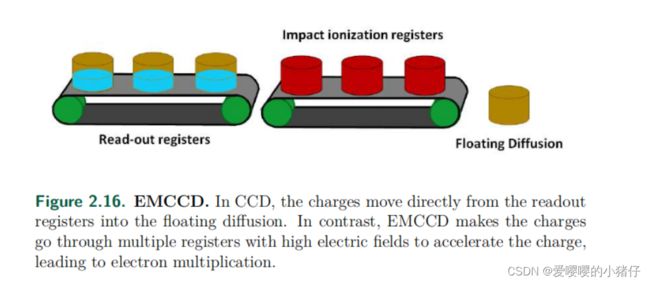
2.5.4 三种技术的比较
3 相机的数学模型
3.1 噪声来源
所有对不同噪声源的解释都是从信号处理的角度进行的。除非有必要,我们不会讨论太多关于导致所有这些噪声源的传感器物理的细节。
3.1.1 光子达到过程
光子的达到是一个随机过程,这种随机性是电磁波粒子性质的直接结果。在图像领域,这叫做散粒噪声。在这部分,我们展示一些光子达到的性质。
假设一个强度为 I ( x , y ; t ) I(x,y;t) I(x,y;t)的光波,到达 x y xy xy平面上的图像传感器。我们对光子的到达做三个假设:
1、单个光子到达面积小于相干区域且小于相干时间的区域的概率与光波的强度 I ( x , y ; t ) I(x,y;t) I(x,y;t)成正比。设 K K K为在时间间隔 Δ t \Delta t Δt和区域 Δ a \Delta a Δa内达到图像传感器的光子数。这个概率是说,对特定的 α \alpha α:
P ( K = 1 ; Δ t , Δ A ) = α Δ t Δ A I ( x , y ; t ) P(K=1;\Delta t,\Delta A)=\alpha \Delta t \Delta A I(x,y;t) P(K=1;Δt,ΔA)=αΔtΔAI(x,y;t)
2、在时间间隔 Δ t \Delta t Δt和区域 Δ a \Delta a Δa内达到的光子数量超过1的可能性可以忽略不计,也就是说: P ( K > 1 ; Δ t , Δ A ) ≈ 0 P(K>1;\Delta t,\Delta A)\approx 0 P(K>1;Δt,ΔA)≈0。因此我们可以写成:
P ( K = 0 ; Δ t , Δ A ) = 1 − α Δ t Δ A I ( x , y ; t ) P(K=0;\Delta t,\Delta A)=1-\alpha \Delta t\Delta AI(x,y;t) P(K=0;Δt,ΔA)=1−αΔtΔAI(x,y;t)
3、光子到达过程在任何非重叠区域或时间间隔内都是相互独立的。
让我们看看光子数量 K K K在任意时间间隔 ( T , T + τ + Δ τ ) (T,T+\tau+\Delta \tau) (T,T+τ+Δτ)到达图像传感器的区域 Δ A \Delta A ΔA的概率分布。由于我们考虑的是 ( x , y ) (x,y) (x,y)附近固定的 Δ A \Delta A ΔA区域,我们将暂时忽略方程中的 Δ A , x \Delta A,x ΔA,x和 y y y。
P ( K = k ; ( T , T + τ + Δ τ ) ) = P ( K = k − 1 ; ( T , T + τ ) ) ⋅ P ( K = 1 ; ( T + τ + Δ τ ) ) + P ( K = k ; ( T , T + τ ) ) ⋅ P ( K = 0 ; ( T + τ , T + τ + Δ τ ) ) P(K=k;(T,T+\tau+\Delta\tau))=P(K=k-1;(T,T+\tau))\cdot P(K=1;(T+\tau+\Delta \tau))\\ +P(K=k;(T,T+\tau))\cdot P(K=0;(T+\tau,T+\tau+\Delta \tau)) P(K=k;(T,T+τ+Δτ))=P(K=k−1;(T,T+τ))⋅P(K=1;(T+τ+Δτ))+P(K=k;(T,T+τ))⋅P(K=0;(T+τ,T+τ+Δτ))
现在使用假设3中的独立性,以及假设1和2中的式子,重写上式,可以得到:
P ( K = k ; ( T , T + τ + Δ τ ) ) = P ( K = k − 1 ; ( T , T + τ ) ) ⋅ α Δ τ I ( T + τ ) + P ( k = k ; ( T , T + τ ) ) ⋅ [ 1 − α Δ τ I ( t + τ ) ] P(K=k;(T,T+\tau+\Delta \tau))=P(K=k-1;(T,T+\tau))\cdot \alpha\Delta \tau I(T+\tau)\\ +P(k=k;(T,T+\tau))\cdot[1-\alpha\Delta \tau I(t+\tau)] P(K=k;(T,T+τ+Δτ))=P(K=k−1;(T,T+τ))⋅αΔτI(T+τ)+P(k=k;(T,T+τ))⋅[1−αΔτI(t+τ)]
重新整理式子可以得到:
P ( K = k ; ( T , T + τ + Δ τ ) ) − P ( K = k ; ( T , T + τ ) ) Δ τ = α I ( t + τ ) [ P ( K = k − 1 ; ( T , T + τ ) ) − P ( K = k ; ( T , T + τ ) ) ] \frac{P(K=k;(T,T+\tau+\Delta \tau))-P(K=k;(T,T+\tau))}{\Delta \tau}=\\ \alpha I(t+\tau)[P(K=k-1;(T,T+\tau))-P(K=k;(T,T+\tau))] ΔτP(K=k;(T,T+τ+Δτ))−P(K=k;(T,T+τ))=αI(t+τ)[P(K=k−1;(T,T+τ))−P(K=k;(T,T+τ))]
让 Δ τ \Delta \tau Δτ趋近于0,我们可以得到:
d P ( K = k ; ( T , T + τ + Δ τ ) ) − P ( K = k ; ( T , T + τ ) ) d τ = α I ( t + τ ) [ P ( K = k − 1 ; ( T , T + τ ) ) − P ( K = k ; ( T , T + τ ) ) ] (3.6) \frac{dP(K=k;(T,T+\tau+\Delta \tau))-P(K=k;(T,T+\tau))}{d\tau}=\\ \alpha I(t+\tau)[P(K=k-1;(T,T+\tau))-P(K=k;(T,T+\tau))]\tag{3.6} dτdP(K=k;(T,T+τ+Δτ))−P(K=k;(T,T+τ))=αI(t+τ)[P(K=k−1;(T,T+τ))−P(K=k;(T,T+τ))](3.6)
然后可以根据定理3.1.1得到解。

这里证明 ( 3.8 ) (3.8) (3.8)是 ( 3.7 ) (3.7) (3.7)的一个解。
将 ( 3.8 ) (3.8) (3.8)带进 ( 3.7 ) (3.7) (3.7),让 θ ( τ ) = ( ∫ T T + τ G ( t ) d t ) \theta(\tau)=(\int_T^{T+\tau }G(t)dt) θ(τ)=(∫TT+τG(t)dt),可以得到:

这和式(3.7)的右侧一样。这里,(a)使用了 d θ ( τ ) d τ = d d τ ∫ T T + τ G ( t ) d t = G ( T + τ ) \frac{d\theta(\tau)}{d\tau}=\frac{d}{d\tau}\int_T^{T+\tau}G(t)dt=G(T+\tau) dτdθ(τ)=dτd∫TT+τG(t)dt=G(T+τ)。
通过 G ( t ) = α I ( t ) G(t)=\alpha I(t) G(t)=αI(t)替换式(3.8),我们得到了(3.6)的解,进一步令 θ = ∫ T T + τ α I ( t ) d t \theta=\int_T^{T+\tau}\alpha I(t)dt θ=∫TT+ταI(t)dt,得:
P ( K = k ; ( T , T + τ ) ) = e − θ θ k k ! P(K=k;(T,T+\tau))=\frac{e^{-\theta}\theta^k}{k!} P(K=k;(T,T+τ))=k!e−θθk
这就是著名的泊松PMF分布。
到目前为止的讨论已经假设我们有一个固定的小面积 Δ a \Delta a Δa和一个更长的时间间隔 τ \tau τ。按照类似的步骤,我们还可以证明同样的结果也适用于更大的区域。在上式的一个更一般的版本中,我们将会有:
θ = ∫ ( x , y ) ∈ A ∫ ∫ T T + τ α I ( x , y ; t ) d t d x d y \theta=\int_{(x,y)\in A}\int\int_{T}^{T+\tau}\alpha I(x,y;t)dtdxdy θ=∫(x,y)∈A∫∫TT+ταI(x,y;t)dtdxdy
3.1.2 相干光和非相干光
假设已知光强 I ( x , y ; t ) I(x,y;t) I(x,y;t),我们可以推导出光子到达过程。然而,这个假设不一定满足,这里需要理解光的相干性。
两个光波在空间或者时间上的同一点具有恒定的相位差,就认为它们是相干的。一个产生所有具有相同相位的光波光源被认为是一个相干光源。
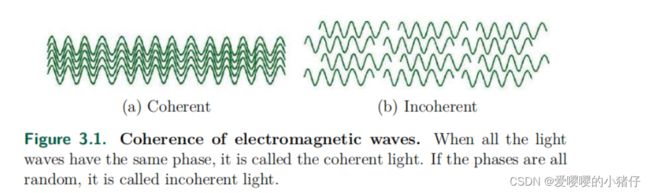
对于一个相干光源,则知道光强的假设是成立的,因此会服从泊松到达分布。然而,对于非相干光,我们只知道它的平均光强因为它的实际光强是一个随机过程,这使得上式的 θ \theta θ是一个随机变量,在这种情况下,得到:
P ( K = k ∣ θ ) = e − θ θ k k ! P(K=k|\theta)=\frac{e^{-\theta }\theta^k}{k!} P(K=k∣θ)=k!e−θθk
然后可以得到:
P ( K = k ) = ∫ θ = 0 ∞ P ( K = k ∣ θ ) P Θ ( θ ) d θ = ∫ θ = 0 ∞ e − θ θ k k ! P Θ ( θ ) d θ (3.12) P(K=k)=\int_{\theta=0}^\infty P(K=k|\theta)P_\Theta(\theta)d\theta=\int_{\theta=0}^\infty \frac{e^{-\theta}\theta^k}{k!}P_\Theta(\theta)d\theta\tag{3.12} P(K=k)=∫θ=0∞P(K=k∣θ)PΘ(θ)dθ=∫θ=0∞k!e−θθkPΘ(θ)dθ(3.12)
这个式子通常被称为曼德尔公式。
非相干光
当光源是非相干时,对于任意的区间 τ \tau τ, P Θ ( θ ) P_{\Theta}(\theta) PΘ(θ)遵循高斯分布:
P Θ ( θ ) = 1 α ( α M β ) M ⋅ ( θ α ) M − 1 e x p { − M θ β } Γ ( M ) (3.13) P_{\Theta}(\theta)=\frac{1}{\alpha}(\frac{\alpha\mathcal{M}}{\beta})^\mathcal{M}\cdot \frac{(\frac{\theta}{\alpha})^{\mathcal{M}-1}exp\{{-\mathcal{M}\frac{\theta}{\beta}}\}}{\Gamma(M)}\tag{3.13} PΘ(θ)=α1(βαM)M⋅Γ(M)(αθ)M−1exp{−Mβθ}(3.13)
这里, M \mathcal{M} M表示测量区间的自由度, β = E ( θ ) \beta=E(\theta) β=E(θ),当只允许时间上的自由度时:
M = [ 1 τ ∫ − ∞ ∞ Λ ( η τ ) ∣ γ ( η ) ∣ 2 d η ] − 1 (3.14) \mathcal{M}=[\frac{1}{\tau}\int_{-\infty}^\infty \Lambda(\frac{\eta}{\tau})|\gamma(\eta)|^2d\eta]^{-1} \tag{3.14} M=[τ1∫−∞∞Λ(τη)∣γ(η)∣2dη]−1(3.14)
其中 γ ( η ) \gamma(\eta) γ(η)是相关的复杂度:
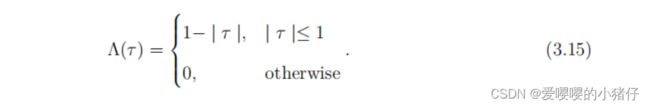
(3.13)-(3.15)的式子可以参照论文:J. W. Goodman, Statistical optics. John Wiley & Sons, 2015.
将(3.13)带入(3.12)得:

(这个式子我也没有看的很明白,应该用了gamma函数的性质)
这个分布被称为负二项分布。这个分布可以用在任意的计数间隔 τ \tau τ。我们来讨论两种特殊情况,当 τ \tau τ相比相干时间特别小或者特别长的时候。
短计数区间
当计数区间 τ \tau τ小于相干时间时, M \mathcal{M} M本质上是统一的,通过让式(3.13)中的 M \mathcal{M} M为1,我们可以发现 θ \theta θ服从指数分布:
P Θ ( θ ) = 1 β e − θ β , θ ≥ 0 (3.17) P_{\Theta}(\theta)=\frac{1}{\beta}e^{-\frac{\theta}{\beta}},\theta\geq0\tag{3.17} PΘ(θ)=β1e−βθ,θ≥0(3.17)
将 M = 1 \mathcal{M}=1 M=1带入(3.16),可以得到:
P ( K = k ) = 1 1 + β ( β β + 1 ) k P(K=k)=\frac{1}{1+\beta}(\frac{\beta}{\beta+1})^k P(K=k)=1+β1(β+1β)k
这个叫做波色=爱因斯坦分布。
长计数区间
对于长的 τ , M → ∞ \tau,\mathcal{M}\rightarrow\infty τ,M→∞,为了反应这一点,对于任意小的 δ \delta δ,令 M = β / δ \mathcal{M}=\beta/\delta M=β/δ,然后(3.16)变成:
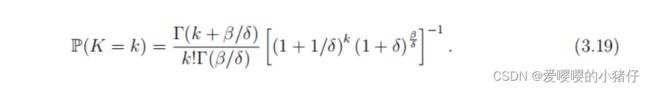
使用 Stirling近似,可以得到:

对于 δ → 0 \delta\rightarrow 0 δ→0,可以得到:

讲这些带入(3.19),可以得到:

又由于 δ → 0 \delta\rightarrow 0 δ→0,所以:
( 1 + k δ β ) k + β δ − 0.5 ≈ e k (1+\frac{k\delta}{\beta})^{k+\frac{\beta}{\delta}-0.5}\approx e^k (1+βkδ)k+δβ−0.5≈ek
所以我们可以得到:
P ( K = k ) = e − β β k k ! P(K=k)=\frac{e^{-\beta}\beta^k}{k!} P(K=k)=k!e−ββk
这就是我们熟知的泊松分布。

在波长为500nm时,我们需要一个10−12s的计数间隔来满足(3.18)的条件,这个间隔太短了。一般来说,我们可以安全地假设,到达图像传感器的几乎所有成像应用中的光子都遵循泊松分布。
3.1.3 到达时间
下面的定理给出光子到达遵循泊松分布时到达时间的概率分布。

证明:
对于一个时间间隔 t t t,泊松随机变量 K K K的概率密度函数可以表示为:
P ( K = k ) = e − γ t ( γ t ) k k ! (3.23) P(K=k)=\frac{e^{-\gamma t}(\gamma t)^k}{k!}\tag{3.23} P(K=k)=k!e−γt(γt)k(3.23)
记 Δ τ \Delta\tau Δτ是两次到达之间的间隙,这意味在 Δ τ \Delta\tau Δτ内没有到达,所以我们可以写成:
P ( Δ τ > t ) = P ( K = 0 ) = e − γ t (3.24) P(\Delta\tau>t)=P(K=0)=e^{-\gamma t}\tag{3.24} P(Δτ>t)=P(K=0)=e−γt(3.24)
我们知道 P ( Δ τ > t ) = 1 − F Δ t ( t ) P(\Delta\tau>t)=1-F_{\Delta t}(t) P(Δτ>t)=1−FΔt(t),这里 F Δ t ( t ) F_{\Delta t}(t) FΔt(t)是达到时间的CDF(累积分布函数)。因此:
F Δ t ( t ) = 1 − e − γ t (3.25) F_{\Delta t}(t)=1-e^{-\gamma t}\tag{3.25} FΔt(t)=1−e−γt(3.25)
对 F Δ t ( t ) F_{\Delta t}(t) FΔt(t)求微分就可以得到需要的概率密度函数。
3.1.4 光子到电子
上一节已经证明了光子的到达过程是一个泊松过程。光子通过光电效应来激发像素中的电子。这个过程如下图所示。
光电效应表明,一个光子只能激发一个电子,然而,并不是所有的光子都能激发电子。然而,并不是所有光子都能激发电子。每个入射光子平均激发 0 ≤ η ≤ 1 0\leq \eta \leq 1 0≤η≤1个电子。 ≤ \leq ≤被称为图像传感器的量子效率。图像传感器在不同的波长下通常具有不同的量子效率。我们通常使用的大多数图像传感器对电磁光谱的可见光范围(400-700纳米)都有很高的灵敏度。

单色光
假设光是单色的,它的光波波长为 λ 0 \lambda_0 λ0,记光强为 I ( x , y , , t ; λ 0 ) I(x,y,,t;\lambda_0) I(x,y,,t;λ0)。我么同样假设光子服从泊松分布。假设到达一个特定像素的光子的平均个数为 β ( λ 0 ) \beta(\lambda_0) β(λ0)。到达传感器k的光子数根据式(3.21)进行概率分布,我们将像素的光子检测建模为伯努利随机变量,检测的概率为 η ( λ 0 ) \eta(\lambda_0) η(λ0)。然后检测到每一个光子概率分布为:
P ( d e t e c t i o n ) = η ( λ 0 ) , P ( m i s s ) = 1 − η ( λ 0 ) P(detection)=\eta(\lambda_0),P(miss)=1-\eta(\lambda_0) P(detection)=η(λ0),P(miss)=1−η(λ0)
探测到的光子数(获产生的电子数)是 K = k K=k K=k伯努利随机变量的和。伯努利随机变量的和遵循二项分布。因此,像素检测到的光子数量 K e = k e K_e=k_e Ke=ke与到达像素的光子数量的分布满足:

P ( K e = k e ) P(K_e=k_e) P(Ke=ke)的概率分布为:


证明:
我们将使用力矩母函数来证明这一点。对于 t ∈ R t\in R t∈R, K e Ke Ke的矩母函数为:
M K e ( t ) = E K e [ e t K e ] = E k { E K e ∣ K [ e t K e ] } (3.31) M_{Ke}(t)=E_{Ke}[e^{tKe}]=E_k\{E_{Ke|K}[e^{tKe}]\}\tag{3.31} MKe(t)=EKe[etKe]=Ek{EKe∣K[etKe]}(3.31)
伯努利随机变量的矩母函数为:
E k { E K e ∣ K [ e t K e ] } = ( 1 − η + η e t ) K (3.32) E_k\{E_{K_e|K}[e^{tKe}]\}=(1-\eta+\eta e^t)^K\tag{3.32} Ek{EKe∣K[etKe]}=(1−η+ηet)K(3.32)
注:关于矩母函数,可以参考博客:https://blog.csdn.net/weixin_48524215/article/details/123162267
因此:
M K e ( t ) = E K [ ( 1 − η + η e t ) K ] = E k [ e log ( 1 − η + η e t ) K ] (3.33) M_{K_e}(t)=E_K[(1-\eta+\eta e^t)^K]=E_k[e^{\log(1-\eta+\eta e^t)K}]\tag{3.33} MKe(t)=EK[(1−η+ηet)K]=Ek[elog(1−η+ηet)K](3.33)
记 s = log ( 1 − η + η e t ) s=\log(1-\eta+\eta e^t) s=log(1−η+ηet),则 E k [ e log ( 1 − η + η e t ) K ] = E k [ e s K ] E_k[e^{\log(1-\eta+\eta e^t)K}]=E_k[e^{sK}] Ek[elog(1−η+ηet)K]=Ek[esK]。再考虑到 K K K的矩母函数,即泊松分布的矩母函数,则:
M K e ( t ) = E K [ e s K ] = e β ( e s − 1 ) = e β ( e l o g ( 1 − η + η e t ) − 1 ) = e β ( 1 − η + η e t − 1 ) = e η β ( e t − 1 ) (3.34) M_{K_e}(t)=E_K[e^{sK}]=e^{\beta(e^s-1)}=e^\beta(e^{log(1-\eta+\eta e^t)}-1)=e^{\beta(1-\eta+\eta e^t-1)}=e^{\eta\beta^{(e^t-1)}}\tag{3.34} MKe(t)=EK[esK]=eβ(es−1)=eβ(elog(1−η+ηet)−1)=eβ(1−η+ηet−1)=eηβ(et−1)(3.34)
通过将 M K e ( t ) M_{Ke}(t) MKe(t)和泊松随机变量的矩母函数作比较,不难看出, K e Ke Ke是以 η β \eta\beta ηβ为均值的泊松分布。
因此可以写成:
P ( K e = k e ) = e − η ( λ 0 ) β ( λ 0 ) ( η ( λ 0 ) β ( λ 0 ) ) k e k e ! (3.35) P(K_e=k_e)=\frac{e^{-\eta(\lambda_0)\beta(\lambda_0)}(\eta(\lambda_0)\beta(\lambda_0))^{k_e}}{k_e!}\tag{3.35} P(Ke=ke)=ke!e−η(λ0)β(λ0)(η(λ0)β(λ0))ke(3.35)
我们已经证明了由单色光源激发的电子数遵循泊松过程。然而,在现实生活中,我们不会经常遇到单色光,很少有例外,比如我们使用激光作为光源。因此,我们也需要将这个结果扩展到非单色光。
非单色光
下图展示了太阳光谱的例子。辐射照度 J ( λ ) J(\lambda) J(λ)可以很容易地转化为光子速率:
Φ ( λ ) = J ( λ ) λ h c \Phi(\lambda)=\frac{J(\lambda)\lambda}{hc} Φ(λ)=hcJ(λ)λ
这里 h h h是普朗克常数, c c c是光速, Φ ( λ ) \Phi(\lambda) Φ(λ)的单位为光子/秒/单位面积/nm。假设 Φ ( λ ) \Phi(\lambda) Φ(λ)在空间上上一致,可以认为它是每个到达图像传感器的光子所属波长的概率分布。
f ( λ ) = Φ ( λ ) ∫ 0 ∞ Φ ( λ ) d λ f(\lambda)=\frac{\Phi(\lambda)}{\int_0^\infty\Phi(\lambda)d\lambda} f(λ)=∫0∞Φ(λ)dλΦ(λ)
对于到达像素的 K K K个光子的每一个,它的波长是满足概率密度函数为 f ( λ ) f(\lambda) f(λ)的随机变量。对于每不同的波长,它到达像素的量子效率都会发生变化。
所以,现在可以写出被像素检测出的光子数目的概率分布:

这里 F k e \mathcal{F}_{k_e} Fke包含了 k e k_e ke个元素的所有子集。这样的分布叫做泊松二项分布。并且我们假设每一个 λ i \lambda_i λi都相互独立。
接下来的定理会给出 P ( K e = k e ) P(K_e=k_e) P(Ke=ke)的概率分布。

证明:
同样使用矩母函数进行证明。
M K e ( t ) = E K { E λ ∣ K { E K e ∣ K , λ [ e t K e ] } } (3.42) M_{K_e}(t)=E_K{\{E_{\lambda|K}\{E_{K_e|K,\lambda}[e^{tK_e}]\}}\}\tag{3.42} MKe(t)=EK{Eλ∣K{EKe∣K,λ[etKe]}}(3.42)
其中, K e ∣ K , λ K_e|K,\lambda Ke∣K,λ是泊松二项分布,它就是将 K K K个独立的拥有不同成功率的伯努利随机变量加起来。因此,对应的矩母函数为:
E K e ∣ K , λ [ e t K e ] ∏ i = 1 K ( 1 − η ( λ i ) + η ( λ i ) e t ) (3.43) E_{K_e|K,\lambda}[e^{tK_e}]\prod_{i=1}^{K}(1-\eta(\lambda_i)+\eta(\lambda_i)e^t)\tag{3.43} EKe∣K,λ[etKe]i=1∏K(1−η(λi)+η(λi)et)(3.43)
进一步得到:
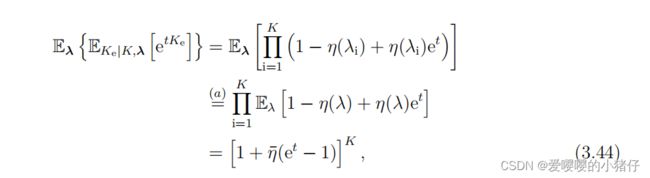
这里(a)是因为假设 λ i \lambda_i λi都是独立的,并且记 η ‾ = E λ ( η ( λ ) ) \overline{\eta}=E_\lambda(\eta(\lambda)) η=Eλ(η(λ))。于是我们可以将 K e K_e Ke的矩母函数写成:
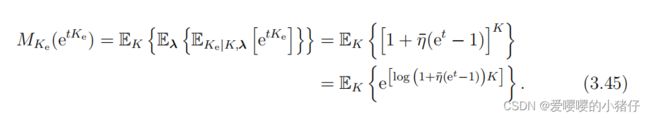
然后遵循定理3.1.3就可以完成相应的证明。
因此,我们已经证明,无论光是否为单色的,由图像传感器检测到的光子数都遵循泊松分布。定理3.1.3和3.1.4中的结果适用于相干光和具有较长计数间隔的非相干光。
3.1.5 暗电流
暗电流值得是在无光照的情况下产生的电流。它是我们不想要的因为它阻碍了我们想要测量的实际光子数量。暗电流减少了动态范围,即可以检测到的光子范围,因为可以存储在像素中的光子数量是有限的,在弱光成像中,当场景中的光子数量与暗电流产生的假电子数量差不多时,暗电流就会产生比较多的问题。暗电流有会很多来源。暗电流是集成时间和运行温度的函数,由于暗电流产生的电荷 K d K_d Kd可以被建模为泊松分布:
P ( K d = k ) = e − β d ( β d ) k k ! P(K_d=k)=\frac{e^{-\beta_d}(\beta_d)^k}{k!} P(Kd=k)=k!e−βd(βd)k
这里 β d = γ d τ \beta_d=\gamma_d\tau βd=γdτ是由暗电流积累的电荷数目的均值。其中, τ \tau τ是集成时间, γ d \gamma_d γd是单位时间内由于暗电流产生的电荷数目。
记总的像素积累的电荷数为 K = K e + K d K=K_e+K_d K=Ke+Kd(这里的 K K K和之前的到达数目 K K K不一样)。所以,假设 β e \beta_e βe是被到达光子激活的电荷数目的均值, β d \beta_d βd是暗电流产生并且积累的电荷数目的均值。像素积累的总电荷数目遵循均值为 β t o t a l = β e + β d \beta_{total}=\beta_e+\beta_d βtotal=βe+βd。
P ( K = k ) = e − ( β e + β d ) ( β e + β d ) k k ! P(K=k)=\frac{e^{-(\beta_e+\beta_d)}(\beta_e+\beta_d)^k}{k!} P(K=k)=k!e−(βe+βd)(βe+βd)k

3.1.6 读出噪声
一旦像素积累的电荷,这些电荷需要被读出。读出噪声通常是指像素的读出电子器件产生的噪声,该噪声通常被建模为高斯噪声:
η r e a d ∼ N ( 0 , δ r e a d 2 ) \eta_{read}\sim N(0,\delta_{read}^2) ηread∼N(0,δread2)
这里 δ r e a d \delta_{read} δread是读出噪声的标准差,其对应的概率分布为:

进一步可以得到传感器读出的模拟信号为:
y = G ⋅ ( K + η r e a d ) (3.50) y=G\cdot(K+\eta_{read})\tag{3.50} y=G⋅(K+ηread)(3.50)
这里 G G G是传感器的转换增益,即将电荷数目转化为传感器读出的电压值。 Y Y Y是泊松-高斯变量。而 Y Y Y的分布是泊松分布和高斯分布的卷积:

下图展示了无读出噪声和不同读出噪声下 Y Y Y的概率分布( β t o t = 2 \beta_{tot}=2 βtot=2)

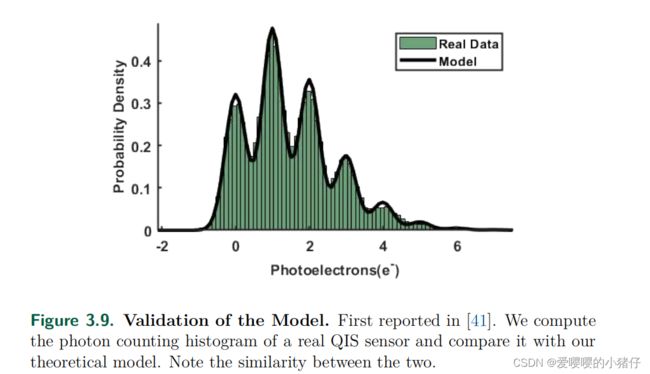
我们使用来自QIS像素的数据验证了是式(3.51)中模型的准确性(如下图所示),通过从一个像素中进行了50000从重复测量来构建光子计数直方图(PCH)。每个度量的积分时间时 50 μ s 50\mu s 50μs。平均光子计数为每像素1.48个光子。ADC使用的是14位的位深度,最小显著性位是 0.05 e − 0.05e^{-} 0.05e−。由于使用的ADC位数为14,所以的大的直方图近似为一个连续体。
其中,我们假定读出噪声为 0.25 e − 0.25e^- 0.25e−,暗电流假定位 0.0068 e − / s 0.0068e^-/s 0.0068e−/s。 β t o t \beta_{tot} βtot的选择使直方图和理论曲线之间的均方差误差最小。由于集成时间只有 50 μ s 50\mu s 50μs,所以我们可以忽略暗电流。从而做出下图
在下图中,我们用仿真数据做出不同强度读出噪声对弱光子图像成像影响的可视化图。我们模拟了三幅图像,平均信号水平为每像素 0.05 e − 0.05e^- 0.05e−,我么假定暗电流为0并且转化增益 G = 1 G=1 G=1。第一张图的读出噪声 δ r e a d = 0 \delta_{read}=0 δread=0,它的唯一噪声来源为散粒噪声。第二张图中我们让读出噪声 δ r e a d = 0.25 \delta_{read}=0.25 δread=0.25。这和第一张图像没有太大的差别。第三章图像中让读出噪声 δ r e a d = 1.5 \delta_{read}=1.5 δread=1.5,则图像的一些细节彻底被破坏了。


关于Remark 3.4,这里推荐一个视频,讲的很清楚:视频链接

3.1.7 固定模式噪声
到目前为止,我们已经研究了时间噪声源,即他们会根据时间变化,并且这些噪声在不同时间的实现是不一样的。也有一些别的噪声,它们不随时间变化,叫做固定模式噪声( fixed pattern noise,FPN)。最常见的两种固定模式噪声是光子相应不一致性(Photon Response Non-Uniformity,PRNU)和暗信号不一致性(Dark Signal Non-Uniformity,DSNU)。
PRNU是不同像素的光子检测效率 η ‾ \overline{\eta} η和转化增益 G G G之间的随机性。PRNU产生于制造过程中的随机性,导致同一传感器像素之间的微小变化。因此,当被一个均匀的光源照明时,每个像素将有一个不同的平均电压读出。PRNU通常是光照的函数,因此是在不同的光水平下计算的。PRNU会在低光照场景下占据主导地位。比如,PRNU的范围可以从 15000 e − 15000e^- 15000e−信号时的 0.1 0.1% 0.1到 10 e − 10e^- 10e−时的 6 6% 6。DSNU是暗电流 β d \beta_d βd中的一个类似的变化。DSNU不依赖于照明,而是依赖于积分时间和工作温度。下图展示了PRNU和DSNU的事例直方图分布。



死像素
在图像传感器中,有时像素停止响应,我们称之为死像素。它们提供零或非常大的输出,与照明无关。这些像素在某种意义上是PRNU的特殊情况,这些图像的乘因子仅为零或一个巨大的常数。
3.1.8 ADC(模数转换)
对ADC建模:

其中, ⌊ ⋅ ⌉ \lfloor\cdot\rceil ⌊⋅⌉是取整函数,O是加到信号上的偏移量,以便我们可以访问负信号值, L A D C L_{ADC} LADC是ADC可以计数的最大整数。L取决于ADC所使用的位深度。例如,如果我们使用一个10位的ADC, L = 2 10 − 1 = 1023 L = 2^{10}−1 = 1023 L=210−1=1023。图像传感器的位深度影响相机运行的速度,因为数据读出传感器的比特率是相机速度的瓶颈。因此,不同的相机和成像技术使用不同的位深度。
满阱容量
满阱容量是像素的性质,并且应该放在在光生电子后介绍。ADC的位数也会影响图像传感器的满阱容量。
通常,在一个像素中,只有有限数量的电子可以被激发,这限制了像素中可以积累的电荷总量,所以积累的电荷会遵循阈值泊松分布,而不是(3.47)中的传统泊松分布。积累的电荷总量不能超过满阱容量,对于一个满阱容量为 L f w L_{fw} Lfw的像素,积累在像素中的总电荷数服从下面的分布:

满阱容量 L f w L_{fw} Lfw依赖于像素的尺寸。更大的像素通常会有更高的满阱容量,反之亦然。下图展示了这种相关性。
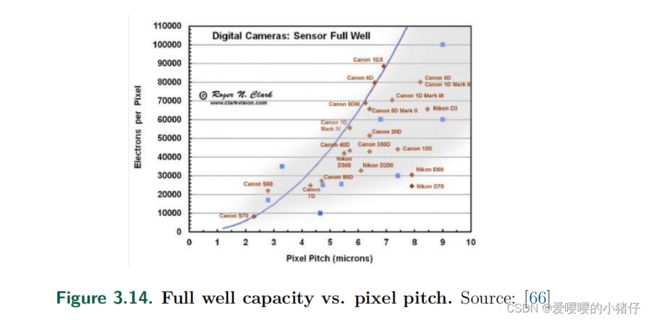
在较高ISO 的情况下,通常像素本身的满阱容量不会影响可读取的最大光生电子数,而是ADC能够读取的最大电子数决定了满阱容量。由于增益因子 G G G在高ISO下是一个很大的数字,因此在数字数据中可以读出的最大光生电子数量变得有限。在这种情况下,满阱容量最终为 L A D C / G L_{ADC}/G LADC/G。单位(bit)的QIS通常只有一个电子的满阱容量。
注:这段文字解释了相机中的高 ISO 设置如何影响图像传感器的满阱容量 (FWC)。 FWC 是像素在饱和前可以容纳的最大电荷量。 在高 ISO 下,FWC 由模数转换器 (ADC) 决定,它将每个像素的模拟信号转换为数字值。 ADC 可输出的数字数字 (DN) 范围有限,该范围除以增益系数 G 以放大高 ISO 下的信号。 这意味着在高 ISO 下每个 DN 可以表示更少的光电子(光子撞击像素产生的电荷单位),因此 FWC 降低。
![]()

3.1.9 其他来源的噪声(只介绍,本文不涉及)
衍射极限
衍射是光通过孔径时弯曲的物理现象。下图展示了显示了当激光发出的红光通过另一个平板上的一个小孔时,在平板上看到的衍射图案。当通过一个圆形孔径时,衍射图案也是圆形的,因此被称为艾里斑。艾里斑的大小取决于光的波长和孔径的大小。孔径越小,艾里斑的尺寸就越大。艾里斑的直径可以这样计算:
x ≈ 2.44 λ f d (3.54) x\approx2.44\lambda\frac{f}{d}\tag{3.54} x≈2.44λdf(3.54)
这里 f d \frac{f}{d} df是镜头的光圈比(镜头焦距和光圈直径的比值), λ \lambda λ是波长。假设采用 f 8 \frac{f}{8} 8f设定,使用波长为 550 n m 550nm 550nm的绿光进行成像,则艾里斑的直径约为 10 μ m 10\mu m 10μm。因此,如果像素间距小于 10 μ m 10\mu m 10μm,则会由于捕捉图像中的衍射而出现模糊,这一点我们可能需要在后续处理中进行处理。如果像素间的间距小于艾里斑的25%,则这两点会变得不可分辨,即像素间距小于 2.5 μ m 2.5\mu m 2.5μm不会增加任何分辨率增益。我们可以使用更大的光圈孔径来使得艾里斑变小。然而,这样会引起失焦模糊——光圈越大,景深越小,失焦模糊的半径就会越大。

串扰
串扰是指一个本应该入射到一个特定像素上的光子最终在一个邻近像素中产生一个光电子的过程。可能发生两种不同的过程。 1.入射到特定像素上的光子可能最终出现在邻近的像素上。这叫做光学串扰。最近的创新,如背面照明传感器(BSI)和微透镜,已经在很大程度上减轻了这种类型的串扰。然而,当像素小于衍射极限时,光学串扰变得不可避免。2.在一个像素中产生的电荷可能会扩散到邻近的一个像素中,这种类型的串扰只能通过精密的图像传感器硬件设计解决。下图展示了这两种串扰。

串扰导致捕获的图像由于引入的模糊而失去分辨率,它也减少了每个像素的颜色信号,导致了颜色通道之间更多的重叠。串扰使颜色重建复杂化,使恢复的图像在颜色上褪色,这需要在图像信号处理管道中处理。
3.2 模拟一个相机
我们已经研究了图像传感器中不同的不同噪声源以及如何建模。现在让我们把它们放在一起,模拟一个相机成像模型。下图显示了我们到目前为止所看到的所有不同噪声源的紧凑版本。

这部分的代码暂时略过。
3.3 模拟相机的性能
到目前为止,我们一直在研究如何建模任何照相机。现在,让我们来看看我们如何分析一个相机的性能。例如,假设我们有两个摄像头。 1.一种传统的具有14位ADC的CMOS图像传感器。 2.一个具有1位ADC的量子图像传感器(QIS)。当然,传感器之间有更多的差异,比如满级容量和帧率。我们必须决定这两个传感器中哪一个更适合我们的应用。为了能够决定这一点,我们需要量化这两个相机的性能。信噪比(SNR)是我们可以用来量化这种性能的一个度量指标。本章的其余部分是关于理解信噪比和推导的数学表达式,我们可以用来量化一个相机的性能。
3.3.1 信噪比(SNR)
信噪比是信号功率与噪声功率的比值:
S N R = s i g n a l p o w e r n o i s e p o w e r SNR=\frac{signal\quad power}{noise\quad power} SNR=noisepowersignalpower
有时会会写成log的形式 10 log 10 S N R 10\log_{10}SNR 10log10SNR。对于数字图像传感器,由于测量的像素值是电压值的模数转换,一个更常见的定义形式是测量均值和标准差的比:
S N R o u t = E [ Y ] V a r [ Y ] (3.57) SNR_{out}=\frac{E[Y]}{\sqrt{Var[Y]}}\tag{3.57} SNRout=Var[Y]E[Y](3.57)
这里, Y Y Y是表示传感器测量值的随机变量, E [ ⋅ ] E[\cdot] E[⋅]是数学期望, V a r [ ⋅ ] Var[\cdot] Var[⋅]表示方差。这种表示的SNR通常叫做output-referred SNR,因为它直接测量了传感器的输出。
输出参考的信噪比便于计算。在最直接的设置下,我们可以访问传感器的模拟数据,并且传感器的输出主要受散粒噪声和读出噪声的影响, Y Y Y将遵循泊松-高斯分布:

这里, β \beta β表示表面积和曝光时间上积分的总通量, σ r e a d \sigma_{read} σread是读出噪声的标准差。假设满阱容量无穷大,因此测量值 Y Y Y永远不会饱和,则 Y Y Y的期望为 β \beta β,方差 V a r [ Y ] = β + σ r e a d 2 Var[Y]=\beta+\sigma_{read}^2 Var[Y]=β+σread2。从而 S N R o u t SNR_{out} SNRout可以表达为:
S N R o u t ( β ) = β β + σ r e a d 2 SNR_{out}(\beta)=\frac{\beta}{\beta+\sigma_{read}^2} SNRout(β)=β+σread2β
如果忽略读出噪声,即 σ r e a d = 0 \sigma_{read}=0 σread=0,我们可以得到一个更简单的表达 S N R o u t ( β ) = β SNR_{out}(\beta)=\sqrt{\beta} SNRout(β)=β。这个被广泛采用的方程式表明,随着场景变得更亮,信号中的增益将会覆盖噪声的随机波动,因此信噪比将会增加。
output-referred SNR的不足
问题的原因是传感器的满阱容量并不是无限的。当然,式(3.57)中 S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)的表达在曝光 β \beta β小于满阱容量时仍然是有效的。然而,如果 β \beta β到达了满阱容量甚至超过了满阱容量,这意味着 E [ Y ] E[Y] E[Y]将停止和 β \beta β一起增长,如下图所示:
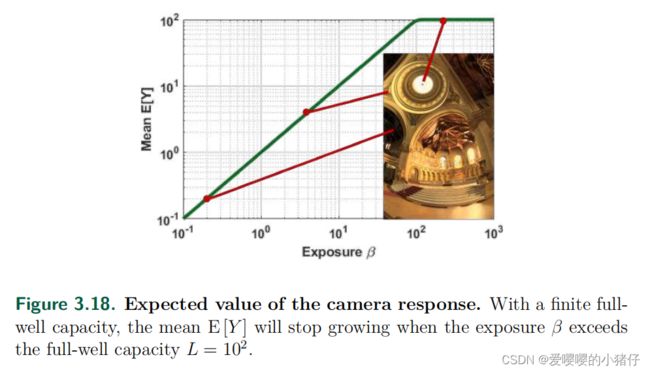
方差 V a r [ Y ] Var[Y] Var[Y]会逐渐降到0因为 Y Y Y不可以超过满阱容量。结果,根据式(3.57), S N R o u t SNR_{out} SNRout会变成无穷。然而,这不可能成立,因为超过饱和的信噪比一定很差。
S N R o u t SNR_{out} SNRout趋于无穷大是由于 S N R o u t SNR_{out} SNRout无法捕获接近和超过满阱容量的行为。这里的普遍采取的方式是通过设置一个零信噪比来创建一个特殊的情况:

式中, L L L为满阱容量。式(3.59)中的定义对于满阱容量足够大的图像传感器就足够了。更重要的是,它便于信号处理。在饱和之前,信噪比呈线性增长(在对数-对数图中)。之后,信噪比为零。
然而,这些年图像传感器的像素尺寸在急剧减小。其对应的满阱容量也越来越小。举例来说,一个单位(bit)的QIS,若它的阈值为 q q q个光子,则测量 Y Y Y变成了二元随机变量:
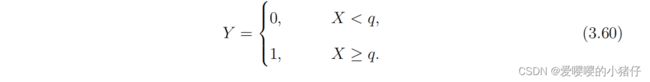
对于更加普遍的 l l l位数字图像传感器,若其满阱容量为 L = 2 l − 1 L=2^l-1 L=2l−1,则其测量变成了:

这里, X ∼ P o i s s i o n ( β ) + G a u s s i a n ( 0 , σ 2 ) X\sim Poission(\beta)+Gaussian(0,\sigma^2) X∼Poission(β)+Gaussian(0,σ2)是ADC前实际的电压。对于这些小的像素,非线性会缺失,因此式(3.59)会无效。
Exposure-referred SNR
当满阱容量 L L L很小时,SNR的推导很困难,2013年,Fossum提出了exposure-referred SNR:
S N R e x p ( β ) = β V a r [ Y ] ⋅ d μ d β (3.62) SNR_{exp}(\beta)=\frac{\beta}{\sqrt{Var[Y]}}\cdot\frac{d\mu}{d\beta}\tag{3.62} SNRexp(β)=Var[Y]β⋅dβdμ(3.62)
其中, μ = E [ Y ] \mu=E[Y] μ=E[Y]

Elgendy和Chan 在论文的补充报告中记录了暴露参考信噪比的直觉。他们认为,导数的 d β / d μ d\beta/d\mu dβ/dμ可以被认为是一个黑盒系统的“传递函数”(这里不是很理解,传递函数不应该是 d μ / d β d\mu/d\beta dμ/dβ么),该系统获取输出的 μ \mu μ,并将其映射回输入的 μ \mu μ。因此, d β / d μ d\beta/d\mu dβ/dμ是这样一个传递函数的增益,该传递函数将噪声从 V a r [ Y ] \sqrt{Var[Y]} Var[Y]扩展到 V a r [ Y ] d β d µ \sqrt{Var[Y]\frac{dβ}{dµ}} Var[Y]dµdβ。它还解释说,如果 β \beta β超过了满阱容量 L L L,衍生物dµ/dβ将变为零,因为 β / \beta/ β/的任何变化都将不再影响 μ \mu μ。因此,信噪比趋于无穷大的问题得到了解决,因为当一个像素饱和时, d μ / d β d\mu/d\beta dμ/dβ=为0,因此信噪比将趋于零。
上述的直觉当然并不严格。在本节中,我们将尝试通过回答四个问题来填补这一理论空白:
(i)定义信噪比的正确方法是什么?以及如何从从理论上推导出 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)?
(ii) S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)和 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)之间的关系是什么?在什么情况下,前者会成为后者的特殊情况?
(iii)对于没有封闭形式表达式的复杂噪声模型,如何通过蒙特卡罗采样技术来数值预测信噪比?(iv) S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)可以提供哪些工具来提高传感器的成像能力?
3.3.2 一些数学基础
截断泊松函数和不完全伽马函数
设 X ∼ P o i s s o n ( β ) X\sim Poisson(\beta) X∼Poisson(β)是一个泊松随机变量,其参数 β \beta β表示在传感器面积和曝光时间上的总曝光积分。期受限于有限的满阱容量为 L L L,超过 L L L, X X X就会处于饱和状态。根据式(3.61)可以定义一个截断泊松变量 Y Y Y的概率质量函数为:

通过构造,随机变量 Y Y Y永远不会取大于 L L L的值。 Y = L Y = L Y=L的概率由泊松尾之和给出,可以通过不完全伽马函数方便地表示,如下图所示。
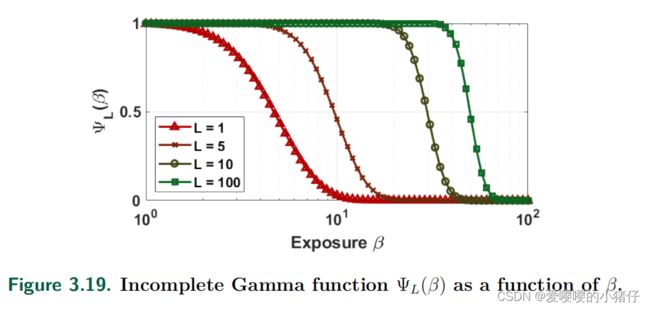
不完全伽马函数定义:

Ψ L ( β ) \Psi_L(\beta) ΨL(β)的一阶微分为:
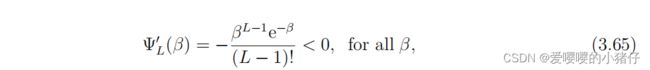
这意味着,对于 β \beta β而言, Ψ L ( β ) \Psi_L(\beta) ΨL(β)是严格单调递减的。通过曲率分析,可以确定最陡的斜率:

令上式为0,可以得到 β ∗ = L − 1 \beta^*=L-1 β∗=L−1。在这个临界点,假设 L > > 1 L>>1 L>>1,则根据Stirling公式可以得到:

因此, Ψ L ′ ( β ∗ ) = − 1 2 π ( L − 1 ) \Psi_L'(\beta^*)=-\frac{1}{\sqrt {2\pi(L-1)}} ΨL′(β∗)=−2π(L−1)1。不完全伽马函数的斜率随着 L L L的增加而减小。

delta方法
当一个随机变量经历一个非线性变换时,它近似于方差。

证明:
考虑泰勒展开:
f ( X ) ≈ f ( μ ) + f ′ ( μ ) ( X − μ ) f(X)\approx f(\mu)+f'(\mu)(X-\mu) f(X)≈f(μ)+f′(μ)(X−μ)
则 ( f ( X ) − f ( μ ) ) (f(X)-f(\mu)) (f(X)−f(μ))的期望为:
E [ ( f ( X ) − f ( μ ) ) 2 ] = E ( f ′ ( μ ) 2 ( X − μ ) 2 ) = [ f ′ ( μ ) ] 2 V a r [ X ] E[(f(X)-f(\mu))^2]=E(f'(\mu)^2(X-\mu)^2)=[f'(\mu)]^2Var[X] E[(f(X)−f(μ))2]=E(f′(μ)2(X−μ)2)=[f′(μ)]2Var[X]
这种近似的有效性取决于二阶项,当随机变量 X X X足够接近 μ \mu μ时,可以假设二阶项很小。这样做的一种方式是,设随机变量 X X X是 N N N个随机变量的样本均值,这样有 X = ( 1 / N ) ∑ n = 1 N Y n X=(1/N)\sum_{n=1}^NY_n X=(1/N)∑n=1NYn,对于全部的 n n n,有 E [ Y n ] = μ E[Y_n]=\mu E[Yn]=μ。对于足够大的 N N N, X X X会集中在 μ \mu μ附近,此时delta方式是有效的。
3.3.3 SNR:统计定义
平均不变性
当定义SNR时,定义信号的信息处理过程是很重要的。在大部分的图像处理问题中,潜在的信号是场景的曝光度 β \beta β。观测是从以 β \beta β为参数的某种分布 p Y ( y ; β ) p_Y(y;\beta) pY(y;β)中获得的随机样本。举例来说,如果 Y ∼ P o s s i o n ( β ) Y\sim Possion(\beta) Y∼Possion(β),那么其对应的分布为 p Y ( y ; β ) = β y e − β / y ! p_Y(y;\beta)=\beta^ye^{-\beta}/y! pY(y;β)=βye−β/y!。
从 Y Y Y中重建信号 β \beta β通常是基于估计器 β ^ ( ⋅ ) \hat{\beta}(\cdot) β^(⋅),一个估计器可以将 Y Y Y映射到估计 β ^ ( Y ) \hat{\beta}(Y) β^(Y)。估计器 β ^ ( ⋅ ) \hat{\beta}(\cdot) β^(⋅)可以是最大似然估计器,最大后验估计器或者其他映射。对于SNR来说,技术需求要求估计器满足平均不变性。


这里可能会混淆平均不变性和无偏估计。一个估计器 β ^ ( Y ) \hat{\beta}(Y) β^(Y)是无偏的如果 E [ β ^ ( Y ) ] = β E[\hat{\beta}(Y)]=\beta E[β^(Y)]=β。而平均不变性则要求 β ^ ( E ( Y ) ) = β \hat{\beta}(E(Y))=\beta β^(E(Y))=β。满足前者的估计器未必满足后者,满足后者的估计器未必满足前者,当 β ^ ( ⋅ ) \hat{\beta}(\cdot) β^(⋅)是线性时,其满足两者。
下面两个例子展示了:对于许多估计器,它们就满足了平均不变性:


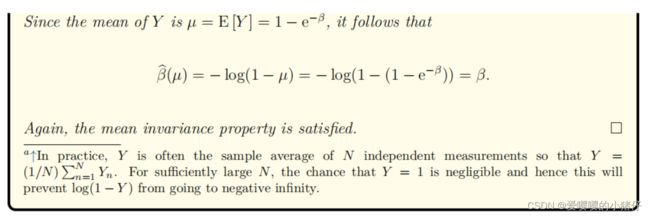
如果估计器满足平均不变性并不难,那么为什么还要引入这个概念呢?从实际的角度来看,测量 Y Y Y的分布可能带有一个复杂的表达式。因此,构造一个估计器 β ^ ( Y ) \hat{\beta}(Y) β^(Y)来最大化可能性并不总是容易的。另一方面,确定平均 E [ Y ] E[Y] E[Y]要容易得多。即使不能解析地推导出 E [ Y ] E[Y] E[Y]的表达式,蒙特卡罗抽样也足以用数值上生成它。一旦均值 E [ Y ] E[Y] E[Y]确定,通过平均不变性就可以确定估计器 β ^ ( Y ) \hat{\beta}(Y) β^(Y),令 μ ( β ) = E [ Y ] \mu(\beta)=E[Y] μ(β)=E[Y],然后可以写成:
β ^ = μ − 1 (3.69) \hat{\beta}=\mu^{-1}\tag{3.69} β^=μ−1(3.69)
回到Example3.1和Example3.2,上面的论证提供了一个过程来构造一个将满足平均不变性原理的估计量。

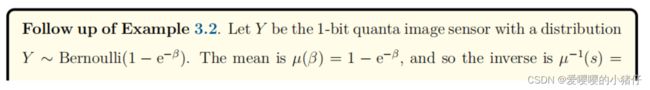
![]()
平均不变性的优点是它绕过了求解优化的复杂性(如最大似然)。另一方面,由于 β ^ \hat{\beta} β^的构造方式,它保证满足均值不变性。
基于到目前为止的分析,似乎很自然地推测,任何极大似然估计量都将满足平均不变性。也就是说 β ^ M L ( E ( Y ) ) = β \hat{\beta}_{ML}(E(Y))=\beta β^ML(E(Y))=β。证明(或给出条件)这个猜想将是有价值的。一个完全任意的估计量 β ^ ( ⋅ ) \hat{\beta}(\cdot) β^(⋅)不适用于信噪比。例如, β ^ ( Y ) = 0 \hat{\beta}(Y)=0 β^(Y)=0对于所有的 Y Y Y都是一个估计器,但它是无用的。因此,可以将均值不变性作为保证一个有意义的信噪比的充分条件。然而,这是否是一个必要的条件是另一个有探索价值的开放性问题。
定义SNR
在描述清楚估计器假设后,对SNR中噪声的讨论是很有必要的。首先,估计器 β ^ ( Y ) \hat{\beta}(Y) β^(Y)是随机的,因为它是 Y Y Y的函数, β ^ ( Y ) \hat{\beta}(Y) β^(Y)相对于真正的确定性参数 β \beta β是波动的。随机性定义了噪声,它实际上是均方误差:
n o i s e = E [ ( β ^ ( Y ) − β ) 2 ] (3.70) noise=E[(\hat{\beta}(Y)-\beta)^2]\tag{3.70} noise=E[(β^(Y)−β)2](3.70)
接下来定义SNR:
![]()
为了让读者相信信噪比的正式定义是有效的,请考虑下面的两个例子:


Exposure-referred SNR
现在要问的一个很自然的问题是, S N R ( β ) SNR(\beta) SNR(β)与 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)和 S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)相比如何。结果表明,如果使用delta方法进行近似, S N R ( β ) SNR(\beta) SNR(β)与 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)相同。这样,我们就可以解释式(3.62)中的“神奇”导数 d μ / d β d\mu/d\beta dμ/dβ从何而来。

证明:
根据delta方法,均方误差可以近似为:
E [ ( β ^ ( Y ) − β ) 2 ] = E [ ( β ^ ( Y ) − β ^ ( μ ) ) 2 ] ≈ [ β ^ ( μ ) ] 2 V a r [ Y ] E[(\hat{\beta}(Y)-\beta)^2]=E[(\hat{\beta}(Y)-\hat{\beta}(\mu))^2]\approx [\hat{\beta}(\mu)]^2Var[Y] E[(β^(Y)−β)2]=E[(β^(Y)−β^(μ))2]≈[β^(μ)]2Var[Y]
由于 β ^ ( μ ) = β \hat{\beta}(\mu)=\beta β^(μ)=β,所以 d β ^ ( μ ) d μ = d β d μ \frac{d\hat{\beta}(\mu)}{d\mu}=\frac{d\beta}{d\mu} dμdβ^(μ)=dμdβ,进一步可得:
E [ ( β ^ ( Y ) − β ) 2 ] = [ d β d μ ] 2 V a r [ Y ] E[(\hat{\beta}(Y)-\beta)^2]= [\frac{d\beta}{d\mu}]^2Var[Y] E[(β^(Y)−β)2]=[dμdβ]2Var[Y]由于 d β d μ = 1 / d μ d β \frac{d\beta}{d\mu}=1/\frac{d\mu}{d\beta} dμdβ=1/dβdμ,所以SNR可以写成:
S N R ( β ) = β E [ ( β ^ ( Y ) − β ) 2 ] = β V a r [ Y ] ⋅ d μ d β = S N R e x p ( β ) SNR(\beta)=\frac{\beta}{\sqrt{E[(\hat{\beta}(Y)-\beta)^2]}}=\frac{\beta}{\sqrt{Var[Y]}}\cdot\frac{d\mu}{d\beta}=SNR_{exp}(\beta) SNR(β)=E[(β^(Y)−β)2]β=Var[Y]β⋅dβdμ=SNRexp(β)
下面证明第二个关系:
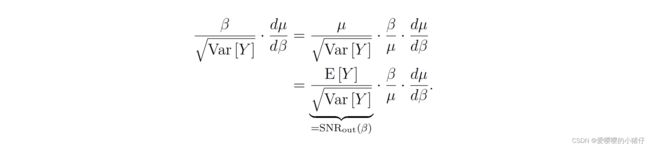
使用单位(bit)QIS阐释信噪比
设 X ∼ P o i s s o n ( β ) X\sim Poisson(\beta) X∼Poisson(β), Y Y Y为服从式(3.60)的随机变量。
首先,考虑 q = 1 q=1 q=1,由于 Y ∼ B e r n o u l l i ( 1 − e − β ) Y\sim Bernoulli(1-e^{-\beta}) Y∼Bernoulli(1−e−β),它的均值 E [ Y ] = 1 − e − β E[Y]=1-e^{-\beta} E[Y]=1−e−β,记 μ = E [ Y ] = 1 − e − β \mu=E[Y]=1-e^{-\beta} μ=E[Y]=1−e−β。如Example 3.1所示,关于 β \beta β的虽大似然估计 β ^ ( Y ) = − log ( 1 − Y ) \hat{\beta}(Y)=-\log(1-Y) β^(Y)=−log(1−Y),它满足均值不变性,导数 d μ / d β d\mu/d\beta dμ/dβ为:
d μ d β = d d β [ 1 − e − β ] = e − β \frac{d\mu}{d\beta}=\frac{d}{d\beta}[1-e^{-\beta}]=e^{-\beta} dβdμ=dβd[1−e−β]=e−β
将其带入到Theorem 3.3.1中,可以的:

对于q > 1的情况,可以利用不完全伽马函数来表示截断泊松随机变量
p Y ( y ; β ) = { 1 − Ψ q ( β ) , y = 1 Ψ q ( β ) = ∑ l = 0 q − 1 β l e − β l ! , y = 0 p_Y(y;\beta)=\left\{ \begin{array}{ll} 1-\Psi_q(\beta),\quad y=1\\ \Psi_q(\beta)=\sum^{q-1}_{l=0}\frac{\beta^le^{-\beta}}{l!},\quad y=0 \end{array} \right. pY(y;β)={1−Ψq(β),y=1Ψq(β)=∑l=0q−1l!βle−β,y=0
上式的期望 E [ Y ] = 1 − Ψ q ( β ) E[Y]=1-\Psi_q(\beta) E[Y]=1−Ψq(β),选择估计器使得 β ^ ( Y ) = − Ψ q − 1 ( 1 − Y ) \hat{\beta}(Y)=-\Psi_q^{-1}(1-Y) β^(Y)=−Ψq−1(1−Y)。这样,平均一致性可以被证实,导数 d μ / d β d\mu/d\beta dμ/dβ为( Ψ q ( β ) \Psi_q(\beta) Ψq(β)的定义参照Definition 3.3.1):

因此,SNR为:

S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)根据定义可以求得:
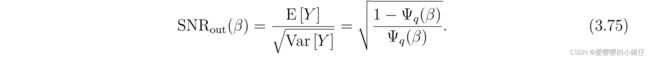
S N R ( β ) ( S N R e x p ( β ) ) SNR(\beta)(SNR_{exp}(\beta)) SNR(β)(SNRexp(β))和 S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)的可视化结果如下图所示:
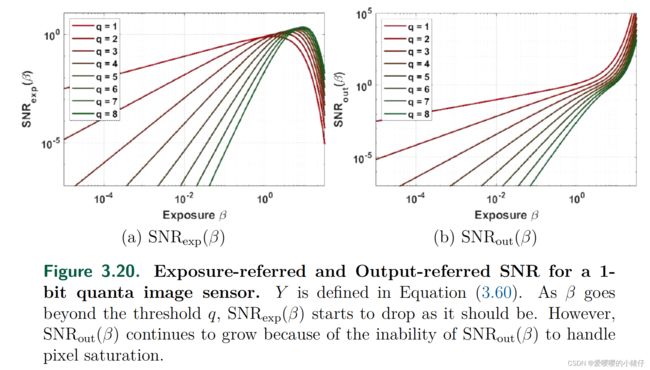
S N R o u t ( β ) SNR_{out}(\beta) SNRout(β)随着 β \beta β的增长而无限增长,这是错误的,因为当 β \beta β增长超过阈值 q q q时,测量值 Y Y Y将更有可能保持在 Y = 1 Y = 1 Y=1。信号会下降,因此最终的信噪比应该会降到零。
3.3.4 有限满阱容量下的 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)
截断泊松分布下的 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)

证明:
Y Y Y的概率密度函数为:

从而 Y Y Y的均值为:

标红处应该为 β k \beta^k βk。
进一步得到导数 d μ / d β d\mu/d\beta dμ/dβ:

对于方差,由于 V a r [ Y ] = E [ Y 2 ] − μ 2 Var[Y]=E[Y^2]-\mu^2 Var[Y]=E[Y2]−μ2,还需要确定 E [ Y 2 ] E[Y^2] E[Y2]:
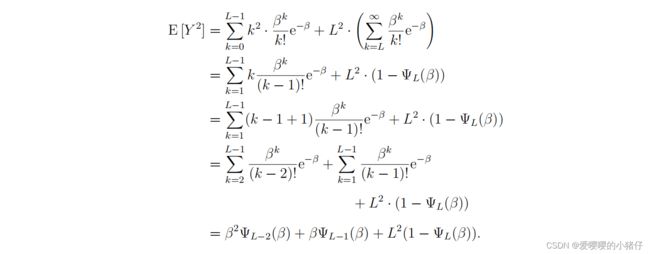
下图显示了不同满阱容量 L L L下的评估结果。与单位(bit)QIS的例子一致,截断泊松分布变量的exposure-referred SNR随着像素饱和下降。
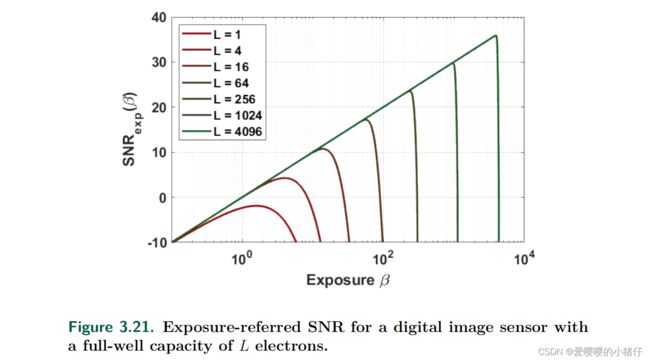
更有趣的是,随着L的增加, S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)在log-log图中变成了一条直线,在饱和后会急剧衰减。这让人想起了式(3.59)中的 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)的启发式定义。然而,对于小的 L L L,光滑过渡是式(3.59)没有预测到的。
饱和后的快速下降有两个原因。首先,log-log图压缩 x x x轴,以便用 β \beta β放大斜率。如果以线性尺度(而不是对数尺度)绘制 x x x轴,急剧的截止将在一个更平滑的过渡中出现。然而,在实践中,曝光总是在对数尺度上显示出来。因此,图3.21中所示的内容是有效的。饱和后下降的第二个原因是由于不完全伽马函数的极限行为。随着 L L L的增加,log-log图中的不完整伽马函数将会有一个越来越尖锐的瞬态,如图3.19所示。
证明:
因为 Y = ( 1 / N ) ∑ n = 1 N Y n Y=(1/N)\sum_{n=1}^{N}Y_n Y=(1/N)∑n=1NYn, E [ Y ] = E [ Y 1 ] E[Y]=E[Y_1] E[Y]=E[Y1]。所以 d μ / d β d\mu/d\beta dμ/dβ的值不变。对于方差,可以很容易地证明 V a r [ Y ] = V a r [ Y 1 ] / N Var[Y]=Var[Y_1]/N Var[Y]=Var[Y1]/N。将其带入到式(3.76)中可以得到:

限制情况
图3.21展示了随着满阱容量 L L L增加, S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β)在log-log图中越来越线性。这种行为可以通过分析不完全伽马函数的极限情况从理论上推导出。
图3.19中,不完整的伽马函数是一个在 L L L处过渡的单调递减函数。假设过渡态的宽度是 δ \delta δ,然后存在一个区间 β ∣ L − δ / 2 ≤ β ≤ L + δ / 2 {β | L−δ/2≤β≤L + δ/2} β∣L−δ/2≤β≤L+δ/2,这样的下限和上限是:
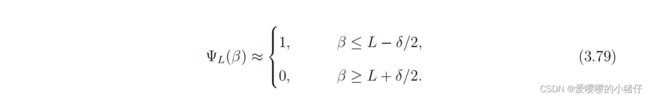
这里,近似“≈”可以基于置信度定义,例如99%的置信度。在这两种极限情况下,可以相应地推导出exposure-referred SNR。

证明:
当 L L L足够大的时候, Ψ L ( β ) \Psi_L(\beta) ΨL(β)和 Ψ L − 1 ( β ) \Psi_{L-1}(\beta) ΨL−1(β)足够接近因而可以被认为近似相等。记 Ψ ( β ) \Psi(\beta) Ψ(β)的值为 Ψ \Psi Ψ。由式(3.79)可知,当 β ≥ L + δ / 2 \beta\geq L+\delta/2 β≥L+δ/2时, Ψ → 0 \Psi\rightarrow 0 Ψ→0,当 β ≤ L − δ / 2 \beta\leq L-\delta/2 β≤L−δ/2时, Ψ → 1 \Psi\rightarrow 1 Ψ→1。在这两种情况下,由于 Ψ \Psi Ψ都是常数,所以 Ψ L ′ ( β ) = 0 \Psi'_L(\beta)=0 ΨL′(β)=0。
当 β ≤ L − δ / 2 \beta\leq L-\delta/2 β≤L−δ/2时:
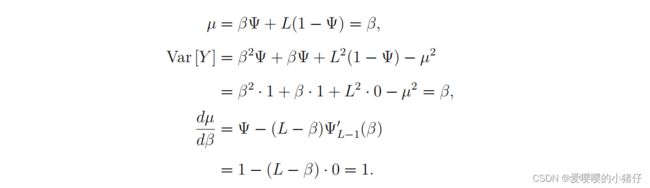
此时的SNR为:

注: μ , V a r [ Y ] , d μ d β \mu,Var[Y],\frac{d\mu}{d\beta} μ,Var[Y],dβdμ的定义参考式(3.77)。
当 β ≥ L + δ / 2 \beta\geq L+\delta/2 β≥L+δ/2时:
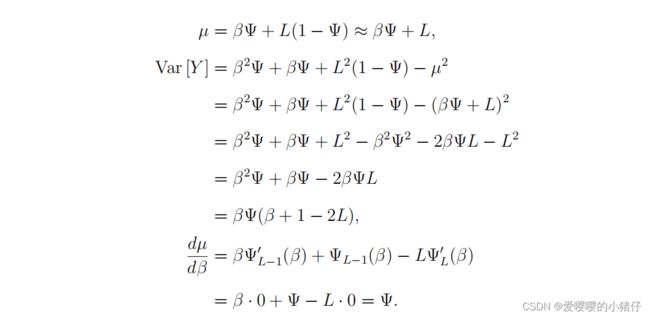
由于 Ψ → 0 \Psi\rightarrow 0 Ψ→0,进一步可得:

结合两种情况的证明,Corollary 3.2得证。
该推论表明,随着 L L L的增加,在对数-对数图中绘制 S N R e x p ( β ) SNR_{exp}(β) SNRexp(β)将给出一个线性响应,然后出现一个突变。这正是在方程(3.59)中所示的output-referred SNR中发生的情况。因此,Theorem 3.3.2是一个广泛定义的output-referred SNR。
截断泊松-高斯分布对应的 S N R e x p ( β ) SNR_{exp}(β) SNRexp(β)
我们找到了截断泊松的SNR表达式。让我们通过添加读出噪声和量化(式(3.52))来使情况更现实一点。我们假设转换增益 G = 1 G = 1 G=1和偏移量 O = 0 O = 0 O=0。在这种情况下,观测值 Z Z Z可以写成:



这里证明略去,可以看Appendix B获得详细证明。
3.3.5 蒙特卡罗仿真
我们可以看到,当我们使噪声模型真实时,SNR的表达式开始变得混乱。随着我们使模型更加现实,解析表达式将明显更具挑战性。一种更合理的方法是采用数值格式来估计近似的SNR。
主要原则
为了计算任何给定分布的 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β),更可行的方法是对由正向模型定义的分布进行抽样:
Y m = f o r w a r d m o d e l ( β ∣ β d a r k , σ r e a d , L ) (3.86) Y_m=forward model(\beta|\beta_{dark},\sigma_{read},L)\tag{3.86} Ym=forwardmodel(β∣βdark,σread,L)(3.86)
这里 m = 1 , . . . , M m=1,...,M m=1,...,M, M M M表示用来计算SNR的蒙特卡罗采样数量。式(3.86)表示从任意前向模型中提取的第 m m m个样本 Y m Y_m Ym。样本 Y m Y_m Ym是信号 β \beta β以及其他参数的函数。当进行蒙特卡罗仿真时,对于任意的 β \beta β,一系列的 { Y 1 , . . . , Y m } \{Y_1,...,Y_m\} {Y1,...,Ym}会被用来计算均值和方差。
具体来说,样本均值是对 E [ Y ] E[Y] E[Y]的估计,样本方差是对 V a r [ Y ] Var[Y] Var[Y]的估计:
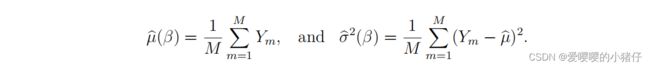
一旦针对每个 β \beta β的 μ ^ ( β ) \hat{\mu}(\beta) μ^(β)被确认,导数 d μ / d β d\mu/d\beta dμ/dβ就可以被近似出来:

进一步可以近似出 S N R e x p ( β ) SNR_{exp}(\beta) SNRexp(β):

Matlab代码
这部分暂时略过
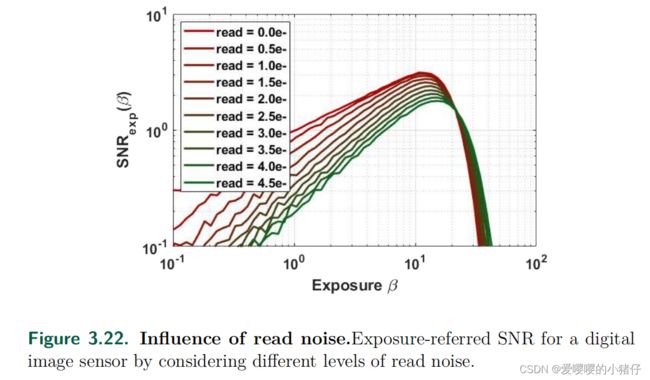
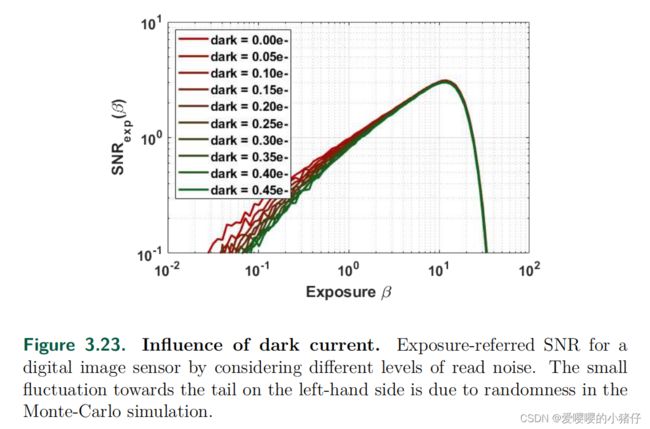
可视化 β d a r k \beta_{dark} βdark和 σ r e a d \sigma_{read} σread的影响
3.3.6 SNR的替代品
Entropy(熵)
如果 Y Y Y是二元的,即 p Y ( 1 ) = 1 − Ψ q ( β ) p_Y(1)=1-\Psi_q(\beta) pY(1)=1−Ψq(β), p Y ( 0 ) = Ψ q ( β ) p_Y(0)=\Psi_q(\beta) pY(0)=Ψq(β),那么熵为:

熵关于 Ψ q ( β ) \Psi_q(\beta) Ψq(β)的导数为:

令上式为0可以得到 Ψ q ( β ) = 1 2 \Psi_q(\beta)=\frac{1}{2} Ψq(β)=21。因此,当 E [ Y ] = 1 − Ψ q ( β ) = 1 2 E[Y]=1-\Psi_q(\beta)=\frac{1}{2} E[Y]=1−Ψq(β)=21时,熵的值最大。这意味着当测量中 50 50% 50为0, 50 50% 50为1时,熵的值最大。因此,如果目标是识别一个阈值 q q q,从而使传感器的性能最大化,那么替代的选择不是优化SNR,而是优化熵。
误码率(Bit Error Rate,BER)
对于1位量子图像传感器,误码率测量了做出错误决策的概率(即,将0声明为1,或将1声明为0)。它可以计算为:

如果 q = 1 / 2 q=1/2 q=1/2,误码率可以简化为:

它并不依赖于 β β β。如果 B E R ( β ) BER(β) BER(β)可以通过经验测量,那么通过反演方程(3.90)就可以估计读取噪声 σ r e a d σ_read σread。对于一个固定的β,我们也可以通过找到一个合适的 q q q来优化公式(3.89)。