动态规划详解

动态规划详解

动态规划是一个很重要的算法，用途很广泛，下面我对动态规划进行入门介绍。

1.基本思想

动态规划的基本思想就是把待解决的问题分成若干的子问题，并且前子问题的解能为后子问题的解提供基础（动态规划的子问题往往不是独立的）。

以我们熟悉的斐波拉契数列为例，递归的方法大家都明白，这个也可以用动态规划来解决。斐波拉契数列第i项（i>2）为前两项之和，f[i]=f[i-1]+f[i-2],按照这个关系一直往后递推。

2.动态规划适用问题

(1)最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

(2)无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

(3)有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

3.求解的步骤

(1)划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

(2)确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。

(3)确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

(4)寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程（包括边界条件）。

核心还是写出这个问题的状态转移方程（状态和状态之间的关系式），斐波拉契的状态转移方程就是：F[i]=F[i-1]+F[i-2]

4.例题

在例题中讲解才能更好的理解算法
例题一：聪明的美食家（最长不降子序列）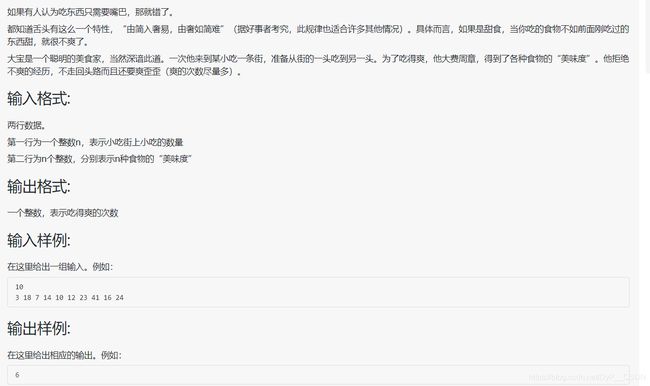
首先我们将问题划分，建立一个数组dp，把这一排美食从1到n划分，数组下标从1到n对应的值就是当前能形成的最长的不降序列，dp初始值为1，因为最短为一个嘛。
下面我们就开始递推，当长度为i时，j从1到i-1开始找，如果j位置的美食度小于i位置的，那么就表示当前能形成的序列比j长度位置形成的序列要大1，若dp[j]+1>dp[i],那么dp[i]目前能形成的序列长度就是dp[j]+1。
状态转换公式：
初值 ：dp[i]=1
dp[i]=max(dp[i],dp[j]+1) arr[i]>=arr[j], j 参考代码：

#include
#include
#include
using namespace std;
int main()
{
	int x;
	cin >> x;
	vector<int>arr(x);//存题目给出序列
	vector<int>dp(x, 1);//存i位置的能构成的最长不降序列
	for (int i = 0; i < x; i++)
	{
		cin >> arr[i];
	}
	for (int i = 0; i < x; i++)
	{
		for (int j = 0; j < i; j++)
		{
			if (arr[j] <= arr[i])
				dp[i] = max(dp[i], dp[j] + 1);
		}
	}
	int m = dp[0];
	for (int i = 0; i < x; i++)
	{
		m = max(m,dp[i]);
	}
	cout << m << endl;
    return 0;
}

上面一个一维的，下面我们讲一个二维情况
例题二：摆花

我们先来分析这个问题，我们要计算n种花共有m盆的摆放方法数，我们建立一个二维数组dp，i,j对应二维数组的行和列，i代表花的种类数，j代表花的盆数，dp[i][j]对应的值即是i种花摆放j盆的方法数，dp[0][0]初始值为1，因为不摆放也是一种方案。
然后我们开始递推:
1种花摆0盆，k带当前种类的花，即只有当这种花摆0盆，剩下的0种花摆0盆这种情况，即dp[1][0]+=d[0][0]
1种花摆放1盆，有当前这种花摆放0盆，剩下的0种花摆1盆；当前的花摆1盆，剩下的0种花摆0盆，即dp[1][1]=dp[0][1]+dp[0][0]
1种花摆放2盆，当前这种花摆0盆，剩下的0种花摆2盆；当前这种花摆1盆，剩下的0种花摆1盆，当前的这种花摆2盆，剩下的零种花摆0盆，即dp[1][2]=dp[0][2]+dp[0][1]+dp[0][0]
…
2种花摆4盆，有当前这种花摆0盆，剩下的一种花摆4盆；当前这种花摆1盆，剩下的一种花摆3盆；当前这种花摆2盆，剩下的一种花摆2盆；当前这种花摆3盆，剩下的1种花摆1盆；当前这种花摆4盆，剩下的1种花摆0盆。即dp[2][4]=dp[1][4]+dp[1][3]+dp[1][2]+dp[1][0]
这个分析为了方便理解没有考虑每种的盆数限制，计算时加上每种的限制就行了，总体思路就是这样。
所以可以得出状态转移方程：A[i][j]=sum{A[i-1][j-k]}
代码：

#include 
#include
using namespace std;
int A[105][105];
int a[105];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	A[0][0]=1; //不摆放花也是一种方案
	for(int i=1;i<=n;i++)//花的种类
	{
		for(int j=0;j<=m;j++)//花的朵数
		{
			for(int k=0;k<=min(a[i],j);k++)//k从0开始表示不一定所有种类的花都要摆上,选择min（a[i],j）是因为第i种花一共只有a[i]盆，要够放 
			{
				A[i][j]=(A[i][j]+A[i-1][j-k])%1000007;
			}
		}
	}
	cout<<A[n][m]%1000007<<endl;
    return 0;
}