13 二叉树:建立存储结构(前序输入次序) &&二叉树专题
目录
首先讲讲指针的引用 *&
然后我们再复习一下typedef的用法。
然后我们来创建二叉树
二叉树的建立
首先二叉树的存储结构(实际用代码体现)分为顺序存储和链式存储两种,但一般情况我们都用链式存储结构。
部分内容转自指针的引用 *&_MAGDB的博客-CSDN博客_指针的引用
首先讲讲指针的引用 *&
以下代码
void shit(student *p)
{
p->data=0;
p=p->next;
}
void shit2(student &*p)
{
p->data=0;
p=p->next;
}请问shit函数和shit2函数有什么区别呢?
对于p->data这一步两个函数都可以修改实参的data值。
但是重点来了
对于p=p->next;这一步,shit不可以让实参中的p指向下一位,而shit2可以改变实参的下一位。
以下为转载。
注意:
能否理解的重点是
如果不是指针引用
指针的指向改变并不能影响原指针的指向
指针指向的值的改变可以影响到原值
也就是说
如果不是指针引用,
形参指针指向改变对实参指针指向没有影响,
形参指针指向值大小改变,实参指针指向值大小随之改变
然后我们再复习一下typedef的用法
。
//以下代码run under c language
typedef struct tagPOINT
{
int x;
int y;
}POINT;
//那么POINT a相当于struct tagPOINT a;
typedef struct tagPOINT
{
int x;
int y;
}POINT,* k;
//那么struct tagPOINT * a相当于k a;
然后我们来创建二叉树
struct student
{
char data;
student* left;
student* right;
};我习惯用student来包装所有目标物,大家习惯就好。
书上一般都是先告诉你遍历的种类,然后再教你如何建立二叉树。
因为下面的建立需要用的遍历的知识。但其实你不知道遍历也可以。我觉得应该先写如何建立二叉树,然后再来介绍遍历的种类。
下面是用的先序遍历来建立二叉链表
//此方法是先序遍历顺序建立二叉链表
void creat(student *&T)
{
char ch;
cin >> ch;
if (ch == '#')
{
T = NULL;
}//但凡输入了#号 就代表这是个空树
else
{
T = new student;
T->data=ch;
creat(T->left);
creat(T->right);
}
}
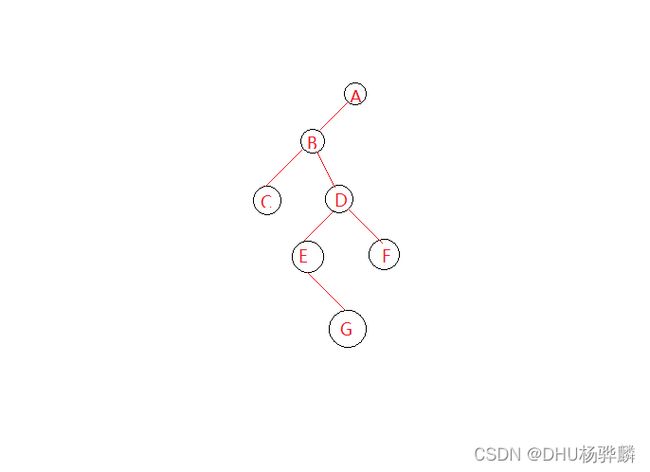
现在举一个例子。
那我们用下面这段代码的时候
应该怎么输入呢?
struct student
{
char data;
student* left;
student* right;
};//此方法是先序遍历顺序建立二叉链表
void creat(student *&T)
{
char ch;
cin >> ch;
if (ch == '#')
{
T = NULL;
}//但凡输入了#号 就代表这是个空树
else
{
T = new student;
T->data=ch;
creat(T->left);
creat(T->right);
}
}
输入:
ABC##DE#G##F###
-----------------
为什么要这样输入呢?为什么输入顺序是这样的呢?建议你去看B站视频看完应该就能够理解了。
【纯干货】三分钟教会你遍历二叉树!学不会举报我!!_哔哩哔哩_bilibili
下面例题一道
13 二叉树:建立存储结构(前序输入次序)
作者: 冯向阳时间限制: 1S章节: DS:树
截止日期: 2022-06-30 23:55:00
问题描述 :
目的:使用C++模板设计并逐步完善二叉树的抽象数据类型(ADT)。
内容:(1)请参照链表的ADT模板,设计二叉树并逐步完善的抽象数据类型。(由于该环境目前仅支持单文件的编译,故将所有内容都集中在一个源文件内。在实际的设计中,推荐将抽象类及对应的派生类分别放在单独的头文件中。参考教材、课件,以及网盘中的链表ADT原型文件,自行设计二叉树的ADT。)
注意:二叉树ADT的基本操作的算法设计很多要用到递归的程序设计方法。
(2)基本操作1:二叉树的二叉链表存储形式的建立,完成后将其加入到二叉树的ADT基本操作集中。
要求设计一个递归算法,将二叉树转化为二叉链表的存储形式。
初始条件:definition给出二叉树T的定义(先序序列。无孩子或指针为空的情形,算法通过特殊分隔符识别(输入)),至少有1个根结点。
输出:按definition构造二叉树的二叉链表。
注意:由于测试数据的显示需建立在二叉树的遍历基础上。因此,请在设计好二叉树的三种遍历算法之后(基本操作2),再进行测试。
参考函数代码:
//建立二叉树的存储结构 (外壳)
template
void CreateTree(BinaryTree
ElemType tmp;
vector
stringstream input_T(str);
while(input_T >> tmp){
t.push_back(tmp);
}
BinaryTreeNode
int num = 0;
root = T.CreateBinaryTree(t, empty, num);
T.SetRoot(root);
}
//建立二叉树的存储结构 (递归部分,成员函数)
template
BinaryTreeNode
ElemType ch = x[n];
n++;
if (ch == empty)
{
return NULL;
}
else
{
BinaryTreeNode
Node->data = ch;
Node->LChild = CreateBinaryTree(x, empty, n);
Node->RChild = CreateBinaryTree(x, empty, n);
return Node;
}
}
二叉树ADT原型参考如下:
/* 二叉表的结点定义 */
template
struct BinaryTreeNode
{
ElemType data;
BinaryTreeNode
BinaryTreeNode() : LChild(NULL), RChild(NULL){} //构造函数1,用于构造根结点
BinaryTreeNode(const ElemType &item, BinaryTreeNode
//函数参数表中的形参允许有默认值,但是带默认值的参数需要放后面
{
LChild = Lptr;
RChild = Rptr;
data = item;
}
ElemType getData(){ return data;} //取得结点中的数据
void SetLChild( BinaryTreeNode
void SetRChild( BinaryTreeNode
void SetData( ElemType value ){ data = value; } //修改结点的data域
BinaryTreeNode
BinaryTreeNode
};
//二叉树
template
class BinaryTree{
private:
BinaryTreeNode
void BinaryTreeDestroy_Cursive( BinaryTreeNode
public:
//无参数的构造函数
BinaryTree():root(NULL){}
//带参数的构造函数
BinaryTree(const ElemType &item){root = new BinaryTreeNode
//生成树
void makeBinaryTree( const ElemType &item, BinaryTree &left, BinaryTree &right);
//拷贝构造函数
//LinkQueue(LinkQueueList
//析构函数
~BinaryTree(){BinaryTreeDestroy();}
//重载函数:赋值
//LinkList
//销毁树
void BinaryTreeDestroy();
//销毁子树
void ChildDestroy(int flag);
//返回二叉树结点的个数
int BinaryTreeSize( BinaryTreeNode
//判断二叉树是否为空
bool BinaryTreeisEmpty() const{return root == NULL;}
//获取根结点元素值
ElemType GetRootData() const{ return root->data;}
//bool Location(ElemType &x, BinaryTreeNode
//设置根结点
void SetRoot(BinaryTreeNode
//获取根结点
BinaryTreeNode
//前序遍历
bool PreOrderTraverse( BinaryTreeNode
//中序遍历
bool InOrderTraverse( BinaryTreeNode
//后序遍历
bool PostOrderTraverse( BinaryTreeNode
//建立二叉树的存储结构
BinaryTreeNode
};
输入说明 :
第一行:表示无孩子或指针为空的特殊分隔符
第二行:二叉树的先序序列(结点元素之间以空格分隔)
输出说明 :
第一行:二叉树先序遍历结果
第二行:二叉树中序遍历结果
第三行:二叉树后序遍历结果
输入范例 :
null
A B null C D null null E null null F null G null H null null
输出范例 :
A,B,C,D,E,F,G,H
B,D,C,E,A,F,G,H
D,E,C,B,H,G,F,A
#include
using namespace std;
bool m = 0;
bool m1 = 0;
bool m2 = 0;
struct student
{
string data;
student* left;
student* right;
};
//此方法是先序遍历顺序建立二叉链表---即二叉树的存储结构(二叉树的实际样子)
void creat(student *&T,string kk)
{
string ch;
cin >> ch;
if (ch == kk)
{
T = NULL;
}//但凡输入了#号 该节点下一位停止
else
{
T = new student;
T->data=ch;
creat(T->left,kk);
creat(T->right,kk);
}
}
//用递归来遍历
void prescan(student *T)//先序遍历
{
if (T == NULL)
{
return;
}
else
{
if (m == 1)
{
cout << ',';
}
cout << T->data;
m = 1;
prescan(T->left);
prescan(T->right);
}
}
void midscan(student* T)//中序遍历
{
if (T == NULL)
{
return;
}
else
{
midscan(T->left);
if (m1 == 1)
{
cout << ',';
}
cout << T->data;
m1 = 1;
midscan(T->right);
}
}
void lastscan(student* T)//后序遍历二叉树
{
if (T == NULL)
{
return;
}
else
{
lastscan(T->left);
lastscan(T->right);
if (m2 == 1)
{
cout << ',';
}
cout << T->data;
m2 = 1;
}
}
void specialscan()//非递归遍历 我现在还不会 会了补上
{
}
int caculate(student *T)
{
if (T == NULL)
{
return 0;
}
else
{
return 1 + caculate(T->left) + caculate(T->right);
}
}
int main()
{
student *head;
string kk;
cin >> kk;
creat(head,kk);
prescan(head);
cout << endl;
midscan(head);
cout << endl;
lastscan(head);
cout << endl;
return 0;
}