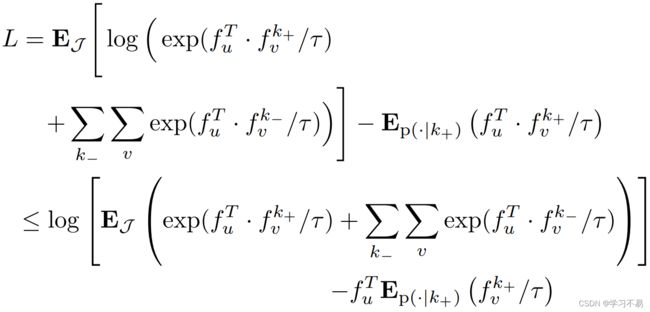CVPR2023 Pseudo-Label Guided Contrastive Learning for Semi-Supervised Medical Image Segmentation

Pseudo-Label Guided Contrastive Learning for Semi-Supervised Medical Image Segmentation

用于半监督医学图像分割的伪标签引导对比学习
Paper：https://openaccess.thecvf.com/content/CVPR2023/html/Basak_Pseudo-Label_Guided_Contrastive_Learning_for_Semi-Supervised_Medical_Image_Segmentation_CVPR_2023_paper.html
Code：https://github.com/hritam-98/PatchCL-MedSeg

Abstract

尽管最近半监督学习（SemiSL）方面的工作在自然图像分割方面取得了巨大的成功，但从有限的注释中学习判别性表示的任务一直是医学图像中的一个悬而未决的问题。

对比学习（CL） 框架使用相似性度量的概念，这对于分类问题很有用，但是它们无法将这些质量表征转移到精确的像素级分割。为此，我们提出了一种新颖的基于半监督补丁的 CL 框架，用于医学图像分割，而不使用任何显式的借口任务。

我们利用 CL 和 SemiSL 的强大功能，其中 SemiSL 生成的伪标签通过提供额外的指导来帮助 CL，而 CL 中学习到的判别类信息则可以实现准确的多类分割。此外，我们制定了一种新颖的损失，可以协同促进学习表示之间的 类间可分离性 和 类内紧凑性 。

在所提出的 CL 框架中，采用了一种使用 平均补丁熵 的新补丁间语义视差映射来引导正负样本采样。对三个公开的多种模式数据集的实验分析揭示了我们提出的方法与最先进的方法相比的优越性。

1 Introduction

医学图像的准确分割为临床医生提供了显着且富有洞察力的信息，以进行适当的诊断、疾病进展和适当的治疗计划。随着最近神经网络的出现，监督深度学习方法在多个医学图像分割任务中取得了最先进的性能[11,36,41]。这可以归因于大型注释数据集的可用性。但是，大规模获得像素级注释通常非常耗时，需要专业知识，并且会产生巨大的成本，因此减轻这些要求的方法非常方便。

基于半监督学习（SemiSL）的​​方法是实现这一目标的有希望的方向，需要非常少量的注释，并为大部分未标记数据生成伪标签，这些伪标签进一步用于训练分割网络 [32, 33 ]。近年来，这些方法因其在下游任务（如分割、目标检测等）中的优越性能而受到广泛认可，不仅在自然场景图像中，而且在生物医学图像分析中[3,4,64]。传统的 SemiSL 方法采用回归、逐像素交叉熵 (CE) 或均方误差 (MSE) 损失项或其变体。但是，这些损失都不会带来类内紧凑性和类间可分离性，从而限制了它们的全部学习潜力。最近在医学视觉中采用自集成策略的 SemiSL 方法[14,44]因其在分割任务中最先进的性能而受到关注。然而，它们是为单个数据集设计的，无法跨域泛化。

无监督域适应（UDA）[18, 61]可以用来解决这个问题，例如，Xie等人[60]提出了一种有效的UDA方法，具有自我训练策略来释放学习潜力。然而，这些方法大多数严重依赖于丰富的来源标签，因此在临床部署中使用有限的标签产生不合格的性能[71]。表征学习是另一种从有限注释中学习的有前途的方法，其中为大型源域上的借口任务训练的模型可以转移到目标域中的下游任务。当前表征学习的进步被归因于对比学习（CL）的兴起[23]，其目的是针对投影嵌入空间中的指定锚点区分相似样本（正样本）和不相似样本（负样本）。通过从大规模未标记数据中学习有用的表示，这个想法导致了自我监督范式的重大进步[9,43,57]。 CL 的基本思想是将语义相似的样本放在一起，并在嵌入空间中将不相似的样本分开。 这是通过适当设计目标函数（也称为对比损失函数）来实现的，该函数优化不同数据点之间的互信息。从借口任务中学到的信息随后可以转移到下游任务，例如分类[62]、分割[53, 66]等。

尽管近年来 CL 框架取得了巨大成功，但它也并非没有问题，主要包括：
（a）[15]中报告了采样偏差和加剧的类冲突，因为由于负样本的无指导选择，语义上相似的实例被强烈对比[ 9]、造成性能不合格；
（b）在 CL 中[21]，将针对现有大规模源域数据集（例如 ImageNet）上的某些代理任务训练的模型调整为目标域的特定下游任务是一种常见且理想的做法。 然而，异构数据集中的显着域变化通常可能会损害整体性能[73]，特别是在医学图像中；
（c）设计一个合适的借口任务可能具有挑战性，并且通常无法跨数据集推广[37]。第一个问题可以通过访问标记样本来解决。例如，[27]表明，包含标签可以显着提高分类性能，但这是在完全监督的情况下进行的。最近有人尝试部分解决最后两个问题，这两个问题在第 2 节中重点介绍。

Our Proposal and Contribution

受这些未解决问题的启发，我们的目标是通过几个新颖的贡献来充分利用 CL 在 SemiSL 领域的潜力：

• 我们通过利用 CL 和 SemiSL 的强大功能，提出了一种新颖的端到端分割范例。在我们的例子中， SemiSL 中生成的伪标签通过为度量学习策略 提供额外的指导 来帮助 CL，而 CL 中重要的 类判别特征学习 则提高了 SemiSL 的多类分割性能 。因此，在医学图像分割任务中， SemiSL 有助于 CL，反之亦然。
• 我们引入了一种新颖的伪标签引导对比损失（PLGCL），它可以挖掘类判别特征，而无需对借口任务进行任何显式训练，从而证明跨多个领域的通用性。
• 我们采用基于 Patch 的 CL 框架，其中正补丁和负补丁是从基于熵的度量中采样的，该度量由 SemiSL 设置中获得的伪标签引导。这可以防止（类冲突），即 CL 中语义相似实例的强制和无指导的对比。
• 经过对来自不同领域的三个数据集的评估，我们的方法被证明是有效的，增加了其通用性和鲁棒性。

2 Related Work

2.1 Semi-supervised Learning

基于 SemiSL 的方法从大量未标记样本中提取有用的表示，同时对一些标记样本进行监督学习。现有 SemiSL 方法采用的策略包括伪标记 [35,42]、一致性正则化 [4,26]、熵最小化 [22, 49] 等。基于伪标记的方法对标记数据进行模型训练，然后生成未标记数据集上的伪标签。 然后使用不确定性引导的细化[50]、随机传播[16]等对生成的伪标签的质量进行微调。 由于为语义分割获取像素级注释的成本很高，因此基于一致性的方法对增强输入强制执行一致的预测图像[17]或增强特征嵌入[39]而不使用注释。熵最小化强制模型对未标记数据输出低熵预测[20]。 整体方法还结合使用这些方法来完成各种任务 [6, 46]。

半监督医学图像分割中另一种广泛使用的方法是 Mean Teacher [47]，它鼓励学生模型和教师模型之间的一致预测。近年来它已扩展到多种 SemiSL 算法。 Yu等人[65]提出了一种不确定性引导的均值教师框架（UA-MT），与转换一致性相结合以提高性能。 Wang等人[52]提出了一个三重不确定性引导的均值教师框架，通过定义两个辅助任务：在均值教师网络之上重建和预测有符号距离场，以帮助模型学习独特的特征以实现更好的预测。杭等人[22]在平均教师网络之上采用了全局局部结构感知熵最小化方法。自训练方法[60,66]结合了来自未标记数据预测的附加信息，可用于提高模型性能。然而，大多数现有的半监督分割方法并没有明确强调类间可分离性问题，因此无意中限制了它们的性能，我们试图在我们提出的工作中解决这一问题。

2.2 Contrastive Learning

近年来，出现了几种强大的（不）相似性学习方法，它们在各种计算机视觉任务中采用对比损失[12,13,37,40]。先前分割中的 CL 方法大多用于自监督预训练，以设计强大的特征提取器，然后将其转移到下游任务 [9, 54]。为了生成正对，这些方法严重依赖于[2, 67]支持的数据增强，尽管值得注意的是大量负数对这些方法的成功至关重要[8]。赵等人[69]设计了一种 CL 策略来挖掘图像级和块级表示之间的关系特征。最近，Wang 等人[55]证明了跨图像对比学习在医学图像分割中的优势。然而，在这种情况下，CL 的一个主要缺点是类冲突问题 [1, 72]——由于朴素 CL 目标的不知情的负面选择，语义相似的补丁会被强烈对比。正如[28]所示，这极大地损害了多类场景中的分割性能。我们的工作旨在通过提出半监督分割中 CL 与一致性正则化的新颖集成来缓解这个问题。与 Boserup 等人 [7] 需要额外的置信网络不同，我们利用伪标签对正负查询进行基于熵的采样，以进行对比学习。

最近的一些进展在半监督环境中采用对比学习[21,25,68]，其中在借口分类任务上训练的模型可以有效地转移到分割任务。然而，他们都没有有效地利用 SemiSL 中的伪标签来改进 CL，反之亦然。此外，这些方法的成功依赖于借口任务的精心设计以及借口任务域和最终分割域之间的最小域转移。我们试图在这项工作中通过在 SemiSL 设置中有效利用 CL 来设计端到端分割框架来解决这些问题。 Chaitanya 等人[10]提出了一种基于局部对比学习的自我训练策略，由伪标签指导，这与我们的工作最接近。 然而，尚不清楚他们提出的像素级 CL 如何在不仔细选择正例和负例的情况下学习判别特征。此外，他们的方法缺乏任何伪标签细化策略，这对于生成伪标签的质量至关重要，并且与度量学习方案直接相关。此外，他们的逐像素 CL 框架存在内存不足问题，限制了它们对一小部分像素进行子采样，并抑制模型学习全局信息。为了解决大多数这些问题，我们提出了以伪标签为指导的分块对比学习，并联合优化 SemiSL 中的 CL 损失和一致性损失，以同时学习特征表示和细化伪标签。

[69] Cross-Level Contrastive Learning and Consistency Constraint for Semi-Supervised Medical Image Segmentation
[55] Exploring Cross-Image Pixel Contrast for Semantic Segmentation
[7] Efficient Self-Supervision using Patch-based Contrastive Learning for Histopathology Image Segmentation
[10] Local contrastive loss with pseudo-label based self-training for semi-supervised medical image segmentation

3 Method

给定一个标记图像集 ${\mathbb{I}}_L$ 及其相应的标记集 ${\mathbb{Y}}_L$ 和一个未标记图像集 ${\mathbb{I}}_U$，其中分别包含 ${\mathcal{N}}_L$ 和 ${\mathcal{N}}_U$ 个图像（其中${\mathcal{N}}_L\ll {\mathcal{N}}_U$）我们引入了一种以伪标签为指导的分片对比学习策略，旨在从 ${\mathbb{I}}_L$ 和 ${\mathbb{I}}_U$ 中学习信息。我们提出的方法可以分为四个步骤：首先，我们定义补丁的生成，由（真或伪）标签的有效利用指导（第3.1小节），然后我们制定一个新的对比损失函数（第3.2小节）。之后，我们定义总体学习目标（第 3.3 节），最后，我们在第 3.4 节中描述伪标签生成和细化策略。

3.1 Class-aware Patch Sampling

让我们将小批量的第 $i$ 个图像表示为 $I_i$ ，包含 $M$ 个像素，其中图像中的第 $m$ 个像素用 $I_i(m)$ 表示；$m\in [1,M]$。我们提出的框架使用编码器和解码器网络 ${\mathcal{E}}_S$ 和 ${\mathcal{D}}_S$，分别由 ${\theta }_{\mathcal{E},\mathcal{S}}$ 和 ${\theta }_{\mathcal{D},\mathcal{S}}$ 参数化，从 $I_i$ 生成伪标签 $Y_i^{\prime }$ ，其等效地表示为类别置信度度量 $C_i$ ，即 $[{\mathcal{E}}_S,{\mathcal{D}}_S]$ : $I_i\to C_i$ 。这里 $C_i={\mathrm{C}}_i^k(m)$ 和 ${\mathrm{C}}_i^k(m)$ 表示属于 $k$ 类的图像 $I_i$ 的像素 $m$ 的置信度，其中 $k=\left\{1,2,..K\right\}$ 和 $K(\ge 1)$ 表示分割图中的类数。此后，将该置信图与 $I_i$ 相乘，以获得关注图像 $I_k^{\prime }=I_i\odot {\mathrm{C}}_i^k$ ，其中 ($\odot$) 表示逐元素乘法。该关注图像需要生成Patch，其中第 $k$ 类的第 $i$ 个关注图像的第 $j$ 个Patch由 $P_{i,j}^k$ 表示。

给定 $k$ 类的锚点补丁，包含 $k$ 类对象（或其某些部分）的所有补丁都被视为正，而来自其他 $(K-1)$ 类的所有补丁都是负的。对大量斑块进行适当采样对于 CL 至关重要。我们可以根据补丁的类别置信度对补丁进行采样，例如，补丁 $P_{i,j}^k$ 的平均置信度计算如下：

高平均补丁置信度表示补丁 $P_{i,j}^k$ 更有可能包含属于 $k$ 类的对象（或其一部分），而接近 0 的值表示相反。中间的值表示任一方向的不确定性。然而，$Av{g}_{i,j}^k$ 仅基于补丁在类 $k$ 上的置信度，它忽略了两个重要的项目：（i）补丁的强度外观信息和（ii）类 $k$ 和其他$(K-1)$类之间的置信不确定性。因此，我们建议根据关注图像 ${I_i^{\prime }}^k$ 计算平均补丁熵。对于补丁$P_{i,j}^k$ ，其平均补丁熵是根据参与图像 ${I_i^{\prime }}^k$ 中的像素强度值计算的，表示为：

是熵函数，${I_i^{\prime }}^k(m)$ 是块内第 $m$ 个像素的强度值。 $En{t}_{i,j}^k$ 反映图像 $i$ 中斑块 $j$ 的三种信息：属于 $k$ 类的置信度、其他$(K-1)$ 类的不确定性以及 $I_i$ 的强度外观（注意，$I_k^{\prime }=I_i\odot {\mathrm{C}}_i^k$)。因此，对于给定的 $k$ 类锚点补丁，所有具有 $n$ 个最接近 $Ent{k}_i^k$ 值的补丁都被视为正值，其余的则为负值。这些补丁通过编码器 ${\mathcal{E}}_S$ 和投影头 ${\mathcal{H}}_S$ 以获得特征嵌入，然后用于下一节中的对比损失公式。锚点的嵌入被视为查询，它与其他补丁的所有其他嵌入（被视为键）形成对比，这是我们 CL 的基础。整个流程如图 1(A) 所示。

Hadamard Product

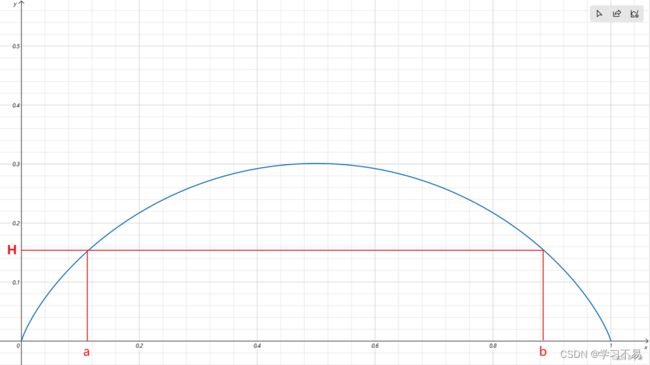
熵函数：
在信息论和统计学中具有重要作用。它常用于衡量二元随机变量的不确定性或信息量。
具体来说，二进熵函数在信息论中用于衡量一个二元随机变量的不确定性。当 x 表示事件发生的概率时，F(x) 表示了在该概率下的平均信息量或不确定性。这个函数的取值范围是 [0,1]，当 x 接近 0 或 1 时，不确定性最大，熵值接近 1；当 x 接近 0.5 时，不确定性最小，熵值接近 0。
$\mathcal{F}(x)=-xlog(x)-(1-x)log(1-x)$ 的函数图像：

3.2 Pseudo-label Guided Contrastive Loss

我们提出了一种新颖的伪标签引导对比损失（PLGCL），假设未标记集 ${\mathbb{I}}_U$ 具有伪标签 ${\mathbb{Y}}_U^{\prime }$ 的可用性（伪标签生成将在第 3.4 小节中解释）以及标记样本$({\mathbb{I}}_L,{\mathbb{Y}}_L$)。 JCL [8] 等先前的工作仅针对给定查询计算正样本分布上的 InfoNCE 损失 [38] 的期望。在我们的例子中，由于类信息以类补丁的形式存在，我们可以对正键和负键的类条件的联合分布进行 InfoNCE 的期望，这是 PLGCL 的基础。

令第 $k$ 类的第 $u$ 个查询补丁表示为 $P_u$，如果 $v$ 为正（即，它与补丁 $P_u$ 具有相同的伪/真类），则其对应的第 $v$ 个关键补丁为 $P_v^{k_{+}}$；否则，它被表示为 $P_v^{k_{-}}$ （与 $k$ 不同的类的负密钥补丁）。我们将 $P_u$、$P_v^{k_{+}}$ 、$P_v^{k_{-}}$ 的嵌入分别表示为 $f_u$、$f_v^{k_{+}}$ 、$f_v^{k_{-}}$ ，使得 $f_u,f_v^{k_{+}},f_v^{k_{-}}\leftarrow {\mathcal{H}}_S({\mathcal{E}}_S(P_u,P_v^{k_{+}},P_v^{k_{-}}))$。令 $f_v^{k_{+}}\sim p(\cdot |k_{+})$ 和 $f_v^{k_{-}}\sim p(\cdot |k_{-})$ 为 InfoNCE 损失相对于联合分布 $\mathcal{J}$ 的期望，在所有类条件密度 $p(\cdot |k_{+})$上和 $p(\cdot |k_{-})$，表示为：

其中 $\tau$ 是温度参数 [12]。方程 4 的封闭式上限可推导为：

最后一个方程是利用凹函数上的 Jensen 不等式获得的，即 $E[log(\cdot )]\le log[E(\cdot )]$。

现在，对所有类条件密度 $p(\cdot |k_{+})$ 和 $p(\cdot |k_{-})$ 使用高斯假设 [8]，我们将它们参数化为 $f_v^{k_{+}}\sim Norm({\mu }_{f_v^{k_{+}}},{\sigma }_{f_v^{k_{+}}})$ 和 $f_v^{k_{-}}\sim Norm({\mu }_{f_v^{k_{-}}},{\sigma }_{f_v^{k_{-}}})$，其中 $\mu$ 和 $\sigma$ 分别表示均值矩阵和协方差矩阵。当 $x\sim Norm(\mu ,\sigma )$ 且 $E_{g(a,b,c,..)}h(a)=E_{g(a)}h(a)$( 时，利用 $E_x(e^{a^{T}x})=e^{a^T\mu +\frac{1}{2}{a}^T\sigma a}$，方程 4 的上限导致我们的分片伪标签引导对比损失：

其中 $\zeta$ 是源自 ${\sum }_v$ 项的缩放因子，即特定类的所有负嵌入的总和。如[8]所述，统计数据在训练后期提供的信息更多，因此使用 $\lambda$ 来衡量 ${\sigma }_{f^{k_{+}}}$ 稳定训练的效果。所提出的损失 ${\mathcal{L}}^{PLGCL}$ 依赖于从 $f_v^{k_{+}}$ 、 $f_v^{k_{-}}$ 对 ${\mu }_{f_v^{k_{+}}}$ 、${\sigma }_{f_v^{k_{+}}}$ 、 ${\mu }_{f_v^{k_{-}}}$ 、 ${\sigma }_{f_v^{k_{-}}}$ 的合理估计。我们通过基于熵的采样策略准确估计正值和负值来解决这个问题（第 3.1 节）。

3.3 The Overall Learning Objective

与所提出的 CL 框架一起，我们的方法可以在半监督环境中从图像中挖掘重要的像素级信息，为此我们采用了学生教师网络 [47]。我们将学生编码器和解码器表示为 ${\mathcal{E}}_S$、${\mathcal{D}}_S$，分别由 ${\theta }_{\mathcal{E},\mathcal{S}}$、${\theta }_{\mathcal{D},\mathcal{S}}$ 参数化，以及教师编码器-解码器模型 ${\mathcal{E}}_T$、${\mathcal{D}}_T$ ，由 ${\theta }_{\mathcal{E},\mathcal{T}}$、${\theta }_{\mathcal{D},\mathcal{T}}$ 参数化。让学生投影头表示为 ${\mathcal{H}}_S$，参数化为 ${\theta }_{\mathcal{H},\mathcal{S}}$。通过学生-教师网络，我们将未标记图像 $I_i\in {\mathbb{I}}_U$ 的一致性成本定义为学生和教师模型输出之间的交叉熵 (CE) 损失：

其中 $I_i^s$ 和 $I_i^w$ 表示输入 $I_i$ 的强增强和弱增强。此外，我们计算来自学生编码器-解码器网络的标记样本 $I_i\in {\mathbb{I}}_L$ 的预测与可用的基本事实 $Y_i\in {\mathbb{Y}}_L$ 之间的监督 CE 损失，如下所示：

最终的目标函数可归结为：

其中 $\mathcal{B}$ 是采样的小批量； ${\mathcal{B}}_L$、${\mathcal{B}}_U$ 分别是小批量中标记和未标记的样本，|·|是设定的基数。在训练期间，学生网络参数通过使用 SGD 优化器最小化公式 8 进行更新，而教师网络参数则使用指数移动平均 (EMA) 进行更新，如下所示：

其中 $t$ 跟踪步数，$\alpha$ 是“平滑系数”[47] 或“动量系数”[23]。

3.4 Pseudo-label Generation and Refinement

如图1所示，我们的方法由三部分组成（A）伪标签引导对比学习，（B）未标记样本的一致性正则化，以及（C）标记样本的监督学习。对比学习部分需要伪标签作为输入。为此，我们使用 50 个 epoch 的小型半监督预热阶段，仅使用等式 8 中的 $L^{Reg}$ 和 $L^{Sup}$ 来生成伪标签。生成并传递图像 $I_i\in {\mathbb{I}}_U$ 的弱增强和强增强分别通过学生和教师模型。我们使用一致性损失 $L^{Reg}$ 来强制确保两个获得的输出之间的一致性（参见公式 6）。此外，我们还计算图像 $I_i\in {\mathbb{I}}_L$ 的学生模型 $Y_i^{\prime }$ 的分割输出和可用的地面实况 $Y_i\in {\mathbb{Y}}_i$ 之间的监督 CE 损失 $L^{Sup}$ 。

预热训练生成初始伪标签，然后在预热阶段后引入对比损失$L^{PLGCL}$，并使用细化的伪标签来训练模型直至收敛。学生模型的参数使用当前网络参数和计算损失的梯度进行迭代更新，而教师网络参数则使用学生模型的 EMA 进行更新（公式 9 和公式 10）。算法 1 总结了总体工作流程。

4 Experiment and Results

我们在具有各种医学成像模式的三个广泛使用的数据集上评估了所提出的方法：MRI、CT 和组织病理学。

4.1 Dataset

（1）ACDC 数据集是心脏 MRI 数据集 [5]，包含 100 个短轴电影 MRI，使用 3T 和 1.5T 机器捕获，并包含三类的专家注释：左心室、右心室（LV、RV）和心肌（MYO）。我们按照[31, 57]的工作将数据集分成 70−10−20 分别作为训练集、验证集和测试集。
（2）KiTS19是一个肿瘤分割数据集[24]，包含210个肾脏CT的标记体积。我们遵循[26]的实验设置，即150用于训练，20用于验证，40用于测试。
（3）结直肠腺癌 (CRAG) 数据集 [19] 包含使用 OmnyxVL120 扫描仪拍摄的 213 张 H&E WS 组织病理学图像。它的图像具有 20 倍物镜放大倍率，分辨率为 0.55 µm/像素。我们按照[43]将数据分成 80−10−10 的训练、测试和验证比率。

4.2 Implementation

我们提出的方法在 PyTorch 环境中实现，并使用具有 32GB RAM 的 Tesla V100 GPU 执行。我们使用三种不同的指标来评估模型性能，即 Dice 相似度得分 (DSC)、Hausdorff 距离 95 (HD95) 和平均对称距离 (ASD) [9]。为了公平比较，我们遵循之前的 SemiSL 作品 [4,10,26]，并使用 10% 和 20% 的标记数据来训练模型，其余部分为未标记数据，除了 KiTS19，我们遵循与[51]在训练时使用 2.5% 和 10% 的图像作为标记。我们使用简单的 U-Net [41] 主干作为编码器-解码器结构，投影头基本上是浅 FC 层 [12]。该模型使用 ADAM 优化器进行收敛，批量大小为 16，学习率为 1e − 4。公式 5 中的 τ 和 λ 分别取 0.2 和 4，如下 [8]。通过验证，方程 9 中的 α、方程 5 中的 β、γ 以及第 3.1 节中基于 n 最近熵的采样中的 n 分别设置为 0.999、0.25、0.2 和 20。对于弱增强，我们使用随机旋转和裁剪，而形态和亮度变化用于强增强[63]。

4.3 Results and Comparison with SOTA

我们使用不同百分比的标记数据进行实验，并将性能与表 1 中以完全监督方式（即使用 100% 的标签）训练的对应数据进行比较。使用不同标签百分比的结果的定性分析如图 2 所示。正如表 1 和图 2 的最后两行所示，我们的方法可以通过使用很少的标签来挖掘判别性特征，从而获得与完全监督的对应结果非常接近的良好结果。

接下来，我们提出的方法与现有最先进的基于 CL 和 SemiSL 的分割方法进行比较。如表 1(a) 所示，我们提出的方法在 MRI 上优于所有 SoTA SemiSL 方法，如 UA-MT [65]、URPC [34]、DTC [32]、MC-Net [59]、SASSNet [29]数据集。正如第 2 节中所讨论的，LCLPL [10] 提出了一种伪标签引导的局部对比学习，这与我们的工作最接近。然而，他们的方法存在无指导的阳性和阴性选择，没有伪标签细化，导致性能次优。相比之下，我们的方法受益于所提出的 PLGCL 损失和基于熵的补丁采样，从而提高了性能。此外，这些边距较大且标签较少（10%），这表明我们的方法从有限的注释中学习的稳健性。对 KiTS19 数据集进行了类似的观察，从表 1(b) 可以明显看出，所提出的方法优于广泛使用的 SemiSL 方法，如 [29,45,56,65]。最近的一种方法 [51] 在 SemiSL 中使用生成贝叶斯深度学习策略产生了第二好的结果，但缺乏挖掘类信息和解决类冲突的能力。大多数其他方法缺乏教师网络通过观察伪标签如何影响学生的反馈机制。然而，在我们的例子中，正则化网络受益于 CL 框架，反之亦然，即使仅使用 2.5% 的标签，也能获得最佳性能。在表 1© 中，我们将我们的工作与 CRAG 数据集上现有的 SoTA 方法的性能进行了比较。在这种情况下，一些最近的方法，如 Double-UA [56]、DTC [32]、UA-MT [65] 产生了良好的结果，但未能在不同的模式中泛化，使我们的方法在所有三个数据集中成为明显的赢家。

4.4 Ablation Study

我们进行了一组消融实验来验证各个组件的有效性。

4.4.1 Effectiveness of PLGCL

我们在使用和不使用伪标签引导对比损失（L P LGCL）的情况下进行了实验。如表2所示，删除PLGCL会显着影响性能，因为它有助于模型学习判别性类别信息，因此PLGCL的引入提高了分割性能。此外，它的功能非常强大，即使没有预热（即在第一个训练周期后立即开始使用伪标签），它仍然可以帮助模型产生相当准确的分割性能（表 2 中的第 3 行）。此外，我们还分析了使用和不使用 L P LGCL 的表示空间的 t-SNE 分解，如图 3 所示。有趣的是，观察 PLGCL 如何随着训练的进行改进特征嵌入的聚类，从而产生良好的类间可分离性和类内紧凑性。另一方面，如果没有 PLGCL，来自不同类的嵌入在特征空间中会相互纠缠。这充分证明了我们提出的方案对于解决 CL 中类冲突这一关键问题的有效性。

4.4.2 Effectiveness of Warm-up Training

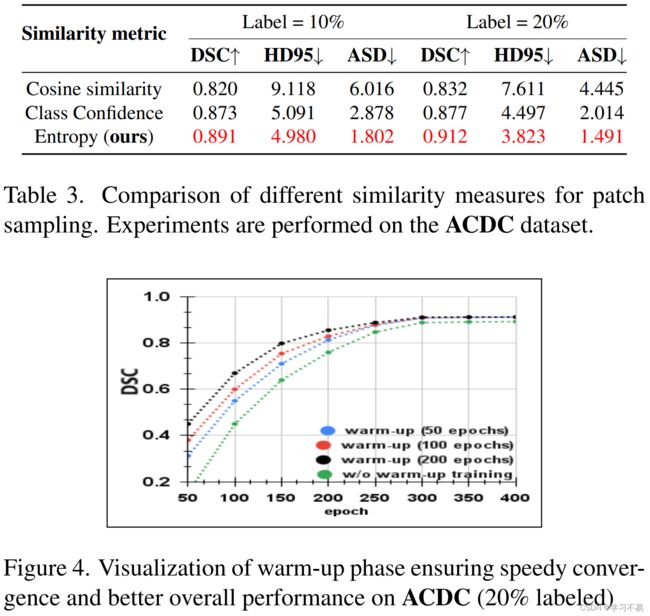
在伪标签生成和细化中，我们使用仅使用 L Sup 和 L Reg 的小型预热阶段，然后进行完整的模型训练。为了确定热身的有效性，我们进行了两组有热身和无热身的实验。首先，模型被预热，之后生成的伪标签用于 CL，并在整个模型训练期间迭代细化。在第二个实验中，我们直接使用第一次迭代中的伪标签进行 CL，而不进行任何迭代细化。如图 4 所示，预热有助于模型在训练的第二阶段更好地初始化，这也得到了[70]的证实。较长时间的预热虽然提供了初始提升，但不一定会提高最终的分割性能（参见图 4）。更好的初始化为 PLGCL 的强有力指导提供了有意义的附加信号，这从表 2 中的观察结果可以明显看出，表 2 中引入预热和 PLGCL 将整个性能提高了 (∼ 7 − 10%)。

4.4.3 Effectiveness of Patch Sampling

我们将我们的补丁采样方法与两个值得注意的方法进行比较：（A）余弦相似度：它是两个补丁之间相似性测量的最明显和最常见的指标。给定两个矢量化补丁 a 和 b，余弦相似度计算如下： Sim(a, b) = a · b/|a||b|。

(B) 类别置信度：对于补丁 P k i,j ，我们计算平均补丁置信度 Avgk i,j （等式 1），具有相似置信度值的补丁被采样为正值，其余的为负值。虽然简单，但 I 'k i 中基于余弦相似度的补丁采样未能产生令人满意的结果，如表 3 所示。然而，基于类置信度的采样性能更好。由于正样本和负样本的采样集并不总是不相交，因此可能会导致较高的误分类率，从而导致性能不佳。我们认为，最好根据类置信图方程 2 所涉及的图像中的熵对正值和负值进行采样，因为它是斑块之间视差映射的更好度量。

5 Conclusion

在这项工作中，我们通过有效利用伪标签在 SemiSL 设置中制定了一种新的 CL 策略。据我们所知，这是首次尝试将 CL 集成到半监督环境中，使用一致性正则化和伪标签进行半监督医学图像分割。当对来自多个领域的三个医学分割数据集进行评估时，所提出的模态不可知模型优于 SoTA 方法，证明了其有效性和普遍性。