【OpenCV入门】第八部分——滤波器

图像平滑处理

图像平滑处理是指在尽量保留原图像信息的情况下，去除掉图像内部的噪声（分布不均匀的、高亮度的像素点）。而用于图像平滑处理的工具就是滤波器。OpenCV提供了种类丰富的滤波器，虽然每种滤波器的实现算法都不同，但每种滤波器都能完成图像平滑处理的操作。本文主要讲解其中的4中滤波器，分别是均值滤波器、中值滤波器、高斯滤波器和双边滤波器。

均值滤波器

噪声与周围像素的差别非常大，导致从视觉上就能看出噪声无法与周围像素组成可识别的图像信息，从而降低了整个图像的质量。如果图像中的噪声都是随机的纯黑像素或者纯白像素，这样的噪声也被称作“椒盐噪声”或“盐噪声”。

以一个像素为核心，核心周围像素可以组成一个 n 行 n 列(简称 n × n) 的矩阵，这样的矩阵结构在滤波操作中被称为“滤波核”。矩阵的行列数决定了滤波核的大小，例如图 9.4 所示的滤波核大小为 3x3，包含 9 个像素;图 9.5 所示的滤波核大小为 5x5，包含 25 个像素。

均值滤波器 (也被称为低通滤波器) 可以把图像中的每一个像素都当成滤波核的核心，然后计算出核内所有像素的平均值，最后让核心像素值等于这个平均值。

上图就是均值波的计算过程。滤波核大小为 3x3，核心像素值是 35，颜色极深，周围像素值都在 110~150之间，因此可以认为核心像素是噪声。将滤波核中的所有像素值相加，然后除以像素个数，就得出了平均值 123 (四舍五入取整)。将核心像素的值改成 123，其颜色就与周围颜色差别不大了，图像就变得平滑了。这就是均值滤波去噪的原理。

OpenCV将均值滤波器封装成了 blur()方法：

dst = cv2.blur(src, ksize, anchor, borderType)

• src： 被处理的图像。
• ksize： 滤波核大小，其格式为(高度，宽度)，建议使用如(3,3)、(5,5)、(7,7)等宽高相等的奇数边长。滤波核越大，处理之后的图像就越模糊。
• anchor： （可选）滤波核的锚点，建议采用默认值，方法可以自动计算锚点
• borderType：（可选）边界样式，建议采用默认值
• dst： 经过均值滤波处理之后的图像。

实例1： 对花朵图像进行均值滤波操作

import cv2

img = cv2.imread("3.png")  # 读取原图
dst1 = cv2.blur(img, (3, 3))  # 使用大小为3*3的滤波核进行均值滤波
dst2 = cv2.blur(img, (5, 5))  # 使用大小为5*5的滤波核进行均值滤波
dst3 = cv2.blur(img, (9, 9))  # 使用大小为9*9的滤波核进行均值滤波
cv2.imshow("img", img)  # 显示原图
cv2.imshow("3*3", dst1)  # 显示滤波效果
cv2.imshow("5*5", dst2)
cv2.imshow("9*9", dst3)
cv2.waitKey()  # 按下任何键盘按键后
cv2.destroyAllWindows()  # 释放所有窗体

结果如下：

中值滤波器

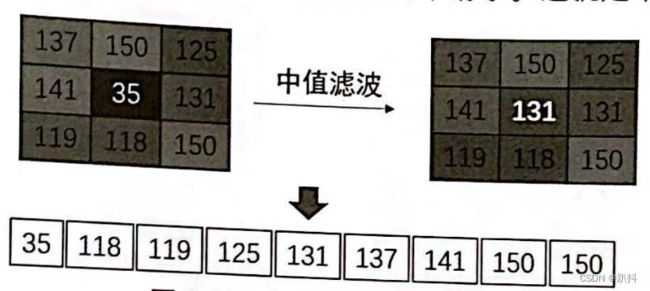
中值滤波器的原理与均值滤波器非常相似，唯一的不同就是不会计算像素的平均值，而是将所有像素值排序，把最中间的像素值取出，赋值给核心像素。

例如上图就是中值滤波的计算过程。滤波核大小为3×3，核心像素值是 35，周围像素值都在110~150之间。将核内所有像素值升序排序，9个像素值排成一队，最中间位置为第5个位置，这个位置的像素值为131。不需再做任何计算，直接把131赋值给核心像素，其颜色就与周围颜色差别不大了，图像就变得平滑了。这就是中值滤波去噪的原理。

OpenCV将中值滤波器封装成了medianBlur()方法：

dst = cv2.medianBlur(src, ksize)

• src： 被处理的图像。
• ksize： 滤波核的边长 (宽度)，必须是大于1的奇数，例如3、5、7等。方法会根据此边长自动创建一个正方形的滤波核。中值滤波器的 ksize 参数是边长，而其他滤波器的 ksize 参数通常为(高,宽)。
• dst： 经过中值滤波处理之后的图像

实例2： 对花朵图像进行中值滤波操作

import cv2

img = cv2.imread("3.png")  # 读取原图
dst1 = cv2.medianBlur(img, 3)  # 使用宽度为3的滤波核进行中值滤波
dst2 = cv2.medianBlur(img, 5)  # 使用宽度为5的滤波核进行中值滤波
dst3 = cv2.medianBlur(img, 9)  # 使用宽度为9的滤波核进行中值滤波
cv2.imshow("img", img)  # 显示原图
cv2.imshow("3", dst1)  # 显示滤波效果
cv2.imshow("5", dst2)
cv2.imshow("9", dst3)
cv2.waitKey()  # 按下任何键盘按键后
cv2.destroyAllWindows()  # 释放所有窗体

结果如下：

中值滤波处理的图像会比均值滤波处理的图像丢失更多细节。

高斯滤波器

高斯滤波也被称为高斯模糊、高斯平滑，是目前应用最广泛的平滑处理算法。高斯滤波可以很好地在降低图片噪声、细节层次的同时保留更多的图像信息，经过处理的图像会呈现“磨砂玻璃”的滤镜效果。

进行均值滤波处理时，核心周围每个像素的权重都是均等的，也就是每个像素都同样重要，所以计算平均值即可。但在高斯滤波中，越靠近核心的像素权重越大，越远离核心的像素权重越小。

高斯滤波的计算过程涉及到卷积运算，会有一个与滤波核大小相等的卷积核。本文不会深入介绍高斯函数以及高斯核的计算方式，仅以 3x3 的滤波核为例，简单地描述一下高斯滤波的计算过程。

卷积核中保存的值就是核所覆盖区域的权重值，其遵循图 9.16 的规律。卷积核中所有权重值相加的结果为 1。例如，3x3 的卷积核可以是如图 9.17 所示的值。随着核大小、标准差的变化，卷积核中的值也会发生较大变化，图 9.17 仅是一种最简单的情况。

进行高斯滤波的过程中，滤波核中像素会与卷积核进行卷积计算，最后将计算结果赋值给滤波核的核心像素。其计算过程如下所示：

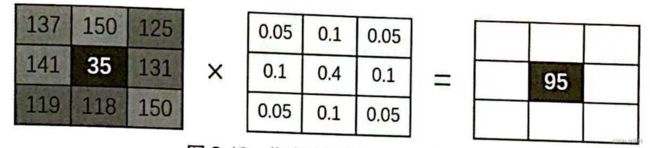
在上图的计算过程中，滤波核中的每个像素值都会与卷积核对应位置的权重值相乘最后计算出9个值，让这9个值相加，再四舍五入取整，就得到了高斯滤波的计算结果。

OpenCV将高斯滤波器封装成了GaussianBlur()方法：

dst = cv2.GaussianBlur(src, ksize, sigmaX, sigmaY, borderType)

• src： 被处理的图像
• ksize： 滤波核的大小，宽高必须是奇数，例如(3,3)、(5,5) 等，
• sigmaX： 卷积核水平方向的标准差。
• sigmaY： 卷积核垂直方向的标准差。修改 sigmaX 或 sigmaY 的值都可以改变卷积材中的权重比例。如果不知道如何设计这两个参数值，就直接把这两个参数的值写成 0，方法就会根据滤波核的大小自动计算出合适的权重比例。
• borderType：（可选）边界样式，建议使用默认值。
• dst： 经过高斯滤波处理之后的图像。

实例3： 对花朵图像进行高斯滤波

import cv2

img = cv2.imread("3.png") # 读取原图
dst1 = cv2.GaussianBlur(img, (5, 5), 0, 0) # 使用大小为5*5的滤波核进行高斯滤波
dst2 = cv2.GaussianBlur(img, (9, 9), 0, 0) # 使用大小为9*9的滤波核进行高斯滤波
dst3 = cv2.GaussianBlur(img, (15, 15), 0, 0) # 使用大小为15*15的滤波核进行高斯滤波
cv2.imshow("img", img) # 显示原图
cv2.imshow("5", dst1) # 显示滤波效果
cv2.imshow("9", dst2)
cv2.imshow("15", dst3)
cv2.waitKey() # 按下任何键盘按键后
cv2.destroyAllWindows() # 释放所有窗体

结果如下：

双边滤波器

不管是均值滤波、中值滤波还是高斯滤波，都会使整幅图像变得平滑，图像中的边界会变得模糊不清。双边滤波是一种在平滑处理过程中可以有效保护边界信息的滤波操作。

双边滤波器会自动判断滤波核处于“平坦”区域还是“边缘”区域：如果滤波核处于“平坦”区域，则会使用类似高斯滤波的算法进行滤波；如果滤波核处于“边缘”区域，则加大“边缘”像素的权重，尽可能地让这些像素值保持不变。

例如 ，图9.23是一幅黑白拼接图像，对这个图像进行高斯滤波，黑白交界处就会变得模糊不清，效果如图9.24所示;但如果对这幅图像进行双边滤波，黑白交界处的边界则可以很好地保留下来，效果如图9.25所示。

OpenCV将双边滤波器封装成了 bilateralFilter() 方法

dst = cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace, borderType)

• src： 被处理的图像。
• d： 以当前像素为中心的整个滤波区域的直径。如果是 d<0，则自动根据 sigmaSpace 参数计算得到。该值与保留的边缘信息数量成正比，与方法运行效率成反比。
• sigmaColor： 参与计算的颜色范围，这个值是像素颜色值与周围颜色值的最大差值只有颜色值之差小于这个值时，周围的像素才会进行滤波计算。值为 255 时，表示所有色都参与计算。
• sigmaSpace： 坐标空间的σ (sigma) 值，该值越大，参与计算的像素数量就越多
• borderType：（可选）边界样式，建议默认。
• dst： 经过双边滤波处理之后的图像。

实例4： 对一幅人脸图像进行”磨皮“

import cv2

img = cv2.imread("girl.png")  # 读取原图
# 双边滤波，选取范围直径为7，颜色差为120
dst2 = cv2.bilateralFilter(img, 7, 120, 100)
cv2.imshow("img", img)  # 显示原图
cv2.imshow("bilateral", dst2)  # 显示双边滤波效果
cv2.waitKey()  # 按下任何键盘按键后
cv2.destroyAllWindows()  # 释放所有窗体

结果如下：

拉普拉斯高通滤波器

锐化又可以称作锐化滤镜，可以加深图像的边缘细节，以达到略微提高图像清晰度的目的，还能让图像中某些色彩更加鲜明。拉普拉斯高通滤波器就是实现锐化效果的一种关键技术。拉普拉斯高通滤波器使用的滤波核如下图所示：

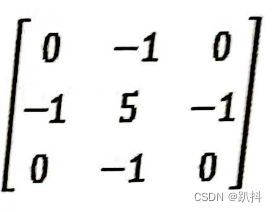
使用这个核进行滤波计算 (同卷积计算) 后，中间的像素值会先乘以5再减去其上、下、左、右四个相邻的像素值。如果中心像素值与四周像素值差别很大，算法就会加深这种差别。从视觉上看，处理之后的图像边缘会呈现出明显的颗粒化。

OpenCV 把拉普拉斯高通滤波器封装成了 filter2D()方法

dst = cv2.filter2D(src, ddepth, kernel, anchor=None, delta=None, borderType=None)

• src： 原始图像。
• ddepth： 输出的图像深度
• kernel： 滤波核。
• anchor：（可选）核的锚点位置，默认为核的中心
• delta：（可选）亮度，默认值为 0。
• borderType：（可选）边界样式。
• dst： 输出的图像。

实例5： 锐化图像

import cv2
import numpy as np

# 拉普拉斯高通滤波的滤波核
def laplacian(img):
    # Laplacian高通滤波算子，5*中间像素值 - 上下左右四个像素值，让像素的梯度越来越大
    kernel = np.array([
        [0, -1, 0],
        [-1, 5, -1],
        [0, -1, 0]])
    dst = cv2.filter2D(img, cv2.CV_32F, kernel)  # 滤波
    dst = cv2.convertScaleAbs(dst)  # 取绝对值
    return dst

# 加载图像
img = cv2.imread('pluto.jpg')
cv2.imshow('Original Image', img)

dst1 = laplacian(img)
cv2.imshow('Laplace', dst1)
cv2.waitKey()
cv2.destroyAllWindows()

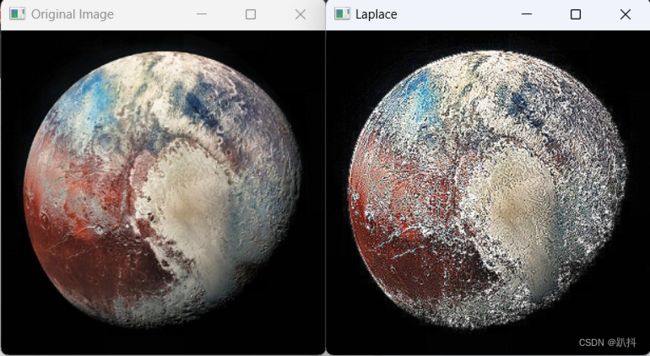
结果如下：