机器人中的数值优化(十二)——带约束优化问题简介、LP线性规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
十八、带约束优化简介
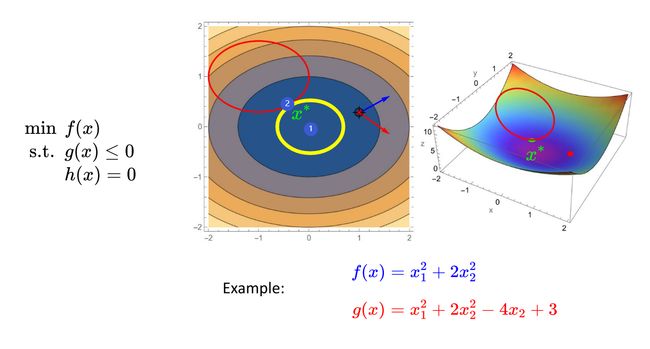
1、简单的例子看有无约束的区别
在如下图所示的表达式f(x)中,无约束优化求得最最优解位于原点处,即图中的①处,若对该问题添加了不等式约束g(x)使解得范围约束在图中的红色椭圆内,此时,求得的最优解,为图中②处
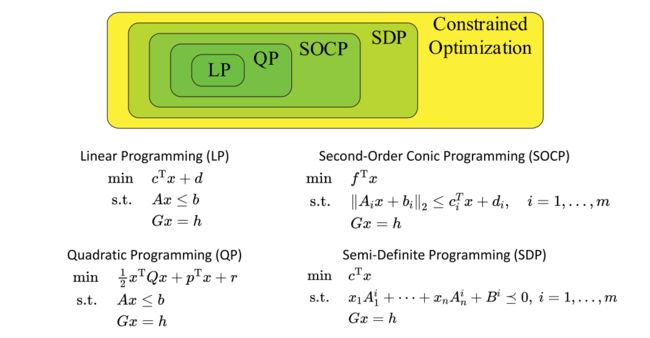
2、带约束优化的类别及复杂性
(1)、线性规划LP
目标函数是线性的,等式约束和不等式约束也是线性的,x是决策变量,c、d、A、b、G、h都是常数矩阵或向量
(2)、二次规划QP
目标函数含有二次项,一般情况下矩阵Q是半正定的,即Q>=0,等式约束或不等式约束一般是线性的。
(3)、锥规划SOCP
目标函数线性的,一般情况下,不等式约束由一个线性表达式的二范数小于等于另一个线性表达式的形式给出。
(4)、半定锥规划SDP
目标函数线性的,一般情况下,不等式约束由广义的不等式形式给出,(喇叭形状的大于等于号是半正定的意思)
(5)、一般形式的带约束的优化问题
一般来说,不加说明的话,LP、SOCP、SDP的目标函数都是线性的,等式约束也是线性的,他们的差别在不等式约束上,一般来说LP的线性不等式约束区域是一个凸多面体,SOCP的不等式约束是一个锥的形状,锥的表面和内部都是可行解。
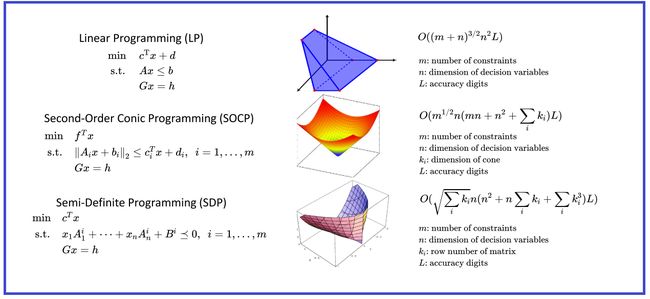
最坏时间复杂度如上图右侧所示,其中m是问题的约束个数,n是x的维度,L是求解精度,比如10的负多少次方,即精确到小数点后几位的位数。SOCP中的ki是锥的维度,m个锥的维度可能不同。SDP中的ki表示,m个广义不等式中Ai或Bi的行向量或列向量的个数。从LP→SOCP→SDP复杂度是增长的。
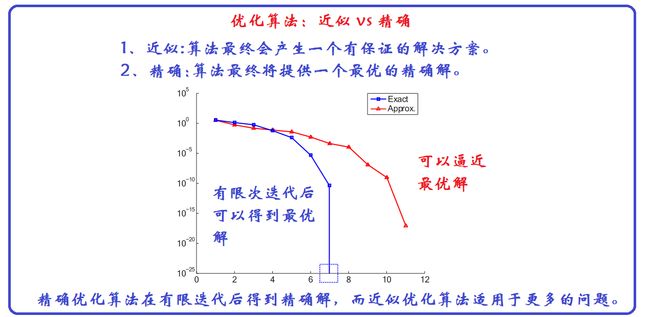
另一类分类方式是按照近似优化算法和精确优化算法划分的,精确优化算法可以在有限次迭代后精确的收敛到最优解,而近似优化算法可以不断的逼近最优解。
十九、低维度LP线性规划
线性规划(Linear Programming,简称LP)是数学规划中的一个重要分支,用于解决在给定一组线性约束条件下,优化一个线性目标函数的问题。线性规划在工程、经济、管理等领域有广泛的应用,它能够找到最优的决策方案,使得目标函数的值达到最大或最小。
一般线性规划问题可以表示为以下标准形式:
最大化或最小化: f = c 1 x 1 + c 2 x 2 + … + c n x n + d f = c_1x_1 + c_2x_2 + \ldots + c_nx_n+d f=c1x1+c2x2+…+cnxn+d
不等式约束为:
a 11 x 1 + a 12 x 2 + … + a 1 n x n ≤ b 1 a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \leq b_1 a11x1+a12x2+…+a1nxn≤b1
a 21 x 1 + a 22 x 2 + … + a 2 n x n ≤ b 2 a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n \leq b_2 a21x1+a22x2+…+a2nxn≤b2
⋮ \vdots ⋮
a m 1 x 1 + a m 2 x 2 + … + a m n x n ≤ b m a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n \leq b_m am1x1+am2x2+…+amnxn≤bm
其中, f f f是要优化的目标函数值, c 1 , c 2 , … , c n c_1, c_2, \ldots, c_n c1,c2,…,cn是目标函数中各项的系数, x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn是决策变量, a i j a_{ij} aij是约束条件矩阵的元素, b i b_i bi是约束条件的右侧常数项。上面的展开式形式可以写成以下的矩阵形式:
min c T x + d s . t . A x ≤ b G x = h \min\quad c^\mathrm{T}x+d\quad\mathrm{s.t.}\quad Ax\leq b\quad Gx=h mincTx+ds.t.Ax≤bGx=h
线性规划的目标是找到一组决策变量 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn,使得目标函数 f f f的值最小化或最大化。同时,这组决策变量要满足所有的约束条件。
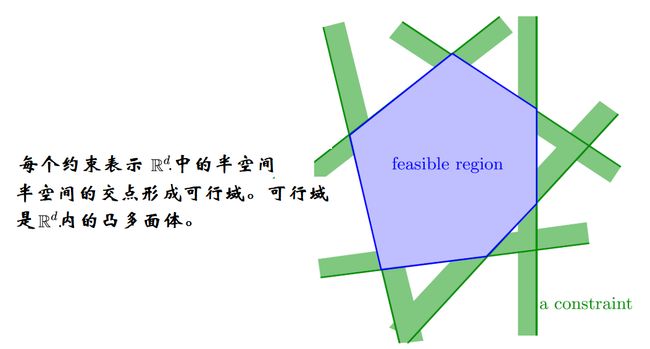
每个不等式约束在几何上限制了一个半空间区域,半空间即线的某一侧区域,所有的半空间取交集即下图中蓝紫色的可行域
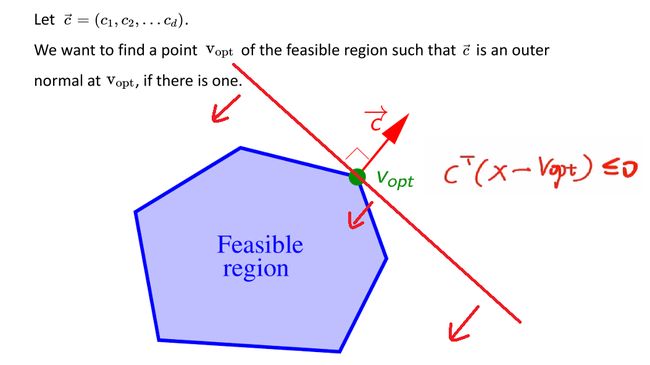
由不等式约束确定了可行域后,在可行域内求解使得 f = c T x + d f=c^\mathrm{T}x+d f=cTx+d最大或最小,d为常量,即在可行域内找到一个使得 c T x c^\mathrm{T}x cTx最大或最小的点 v o p t v_{opt} vopt,使这样一个内积运算的值最大,即在可行域内找一个点 v o p t v_{opt} vopt,构成一个向量x,使得其在c方向上的投影最大。
此时,最大值 c T v o p t > = c T x c^\mathrm{T}v_{opt} >= c^\mathrm{T}x cTvopt>=cTx,其中x是可行域内任意一点,由该表达式可确定如下图红线及箭头所表示的半空间,该半空间包含整个可行域,容易看出,LP问题的最优解 v o p t v_{opt} vopt常位于多边形区域内的某个顶点上。
工程中的许多优化问题都是线性规划。其中一个比较精确的实用算法是单纯形算法(Simplex Method)。单纯形算法虽然是精确的,但在最坏的情况下,其复杂度可能是随问题的参数指数增长的。也有一些伪多项式算法,比如内点法(Interior point methods,IPM),只能提供近似解,计算强度也比较大。一般只在规模很大的情况下才用内点法。在路径规划中,常处理维度较低(如1<=d<=10),但约束个数较多的问题(m很大),往往需要高效率的去求解一些精确解。
(1)一维情况
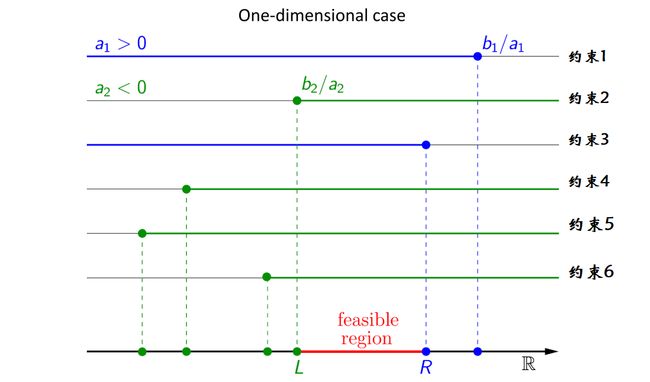
对于下面例子中给出的一维的情况,很容易在线性时间内(O(n))得到其精确解,其中c、a1 ~ an,b1 ~ bn 为一维常数,x为一维变量
假设存在如下图所示的6个不等式约束,很容易得到如下图中红色区域所示的可行域
(2)二维情况
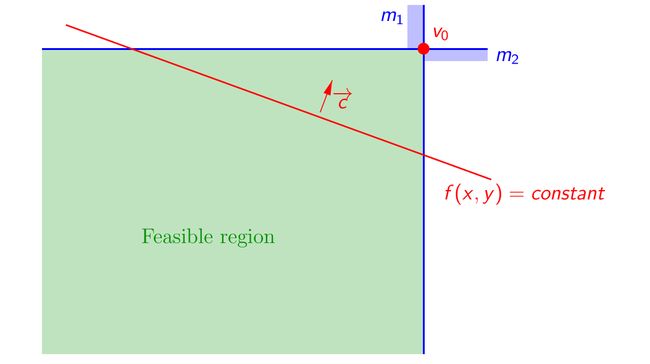
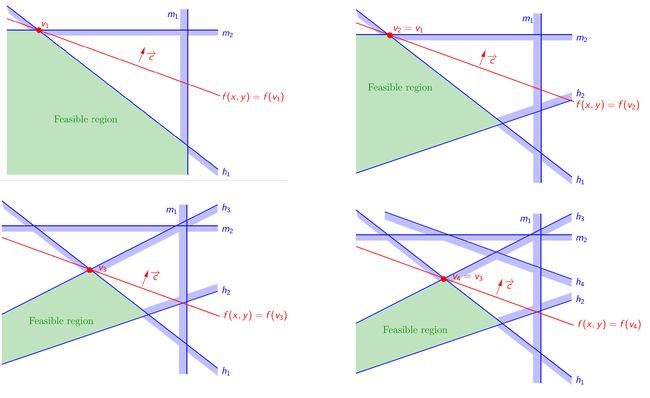
对于下图中所示的二维的情况,两个不等式约束对应的半空间的交集为可行域,即图中绿色区域,c和x都是二维的,目标函数在红线的上侧取得最大值,可得精确解为图中的v0点。
若此时加入一个新的不等式约束h1,此时可行域变为下图所示的绿色区域,加入约束h1之前得到的最优解v0已经不在可行域中,此时目标函数的最优的精确解变为v1点,易知v1点必然位于新加入的约束h1的某个顶点处,再加入新的约束h2后,由于加入约束h2之前的最优解v1依然在当前可行域中,此时的精确解v2=v1,即加入新约束h2后,最优解没有改变,依次类推,再加入新的约束h3后,精确解变为v3,再加入新的约束h4后,精确解为v4=v3。
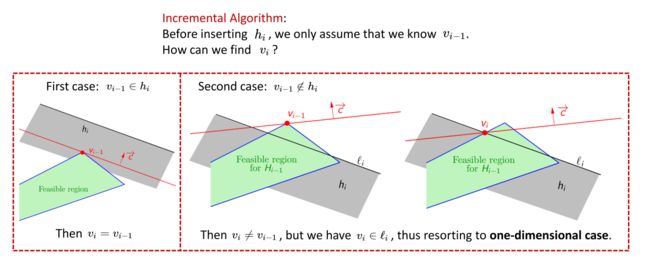
我们对上述过程进行总结,当我们加入一个新的约束 h i h_i hi时,若已知在约束 h 1 h_1 h1 ~ h i − 1 h_{i-1} hi−1下的最优解为 v i − 1 v_{i-1} vi−1,基于这些信息,如何获取加入新的约束 h i h_i hi后的最优解 v i v_i vi,可分为两种情况:
① 若 v i − 1 v_{i-1} vi−1属于新加入的约束 h i h_i hi对应的半空间内,即加入新约束 h i h_i hi后, v i − 1 v_{i-1} vi−1依然在可行域中,此时最优解不变, v i v_{i} vi= v i − 1 v_{i-1} vi−1
② 若 v i − 1 v_{i-1} vi−1不属于新加入的约束 h i h_i hi对应的半空间内,即加入新约束 h i h_i hi后, v i − 1 v_{i-1} vi−1已经不在可行域中了,此时新的最优解 v i v_{i} vi必然位于新加入的约束 h i h_i hi的边界与之前某个约束的边界相交的顶点上,退一步来说,此时新的最优解 v i v_{i} vi必然位于新约束 h i h_i hi的边界 l i l_i li上,此时,我们可以把之前所有的约束 h 1 h_1 h1 ~ h i − 1 h_{i-1} hi−1投影到 l i l_i li上,转化为上面介绍的一维的情况,即在一维线区域 l i l_i li上寻求满足各个约束投影的区间的交集,再配合目标函数,即可得到此时的最优解 v i v_{i} vi。
如果我们随机化约束条件的输入顺序,采用以上增量式方法进行求解,理论上期望的时间复杂度是线性的。
可以使用Fisher-Yates算法对约束条件的顺序进行打乱,Fisher-Yates算法的目标是给定一个n,随机生成一个1 ~ n 的排列,给定n后,有n!,即n的阶乘种可能的排列,Fisher-Yates算法生成任意一种排列的概率是相同的,每种排列的可能性都是1/(n!)
用C++实现时,可以使用 < random >库来实现生成1~m中任意一个整数的功能,来供Fisher-Yates算法调用。
Fisher-Yates算法的流程如下:
①、首先初始化一个1~n的序列,该序列中第几个位置上的数就是几,如序列第n的位置上存放的数值就是n。
②、随机生成一个1~n之间的整数k1,将序列第k1位置上存放的数值,与序列第n个位置上存放的数值进行交换。
③、随机生成一个1~(n-1)之间的整数k2,将序列第k2位置上存放的数值,与序列第(n-1)位置上存放的数值进行交换。
…
…
…
依次类推,直至随机生成1~2之间的一个数(kn-1),将序列第(kn-1)位置上存放的数值,与序列第2个位置上存放的数值进行交换。完成后,Fisher-Yates算法就生成了一个由整数1 ~ n构成 的排列。
(3)更一般的d维情况(d一般是比较小的个位数)
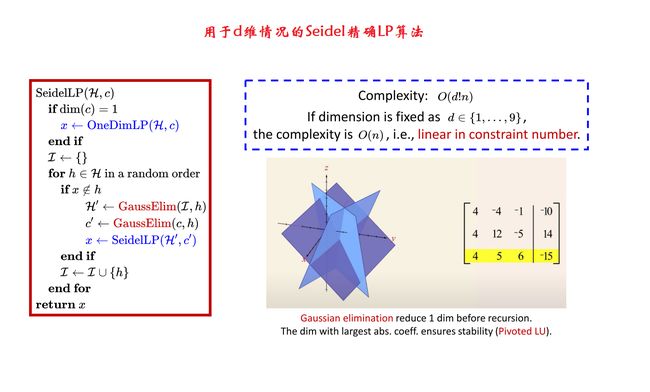
d维的LP线性规划的主要思想是,d维的线性规划在遇到新加入的超平面是Exact时,将其转换成d-1维的线性规划,这跟上面2维线性规划时转换成1维线性规划的思想是相同的,这种思想有点像递归的思想。
上图中给出的伪代码中,输入参数H即不等式约束 a T x < = b a^\mathrm{T}x<=b aTx<=b,也即一系列半空间,输入参数c即 c T x c^\mathrm{T}x cTx中的系数,如果此时c的维度是一维的,则直接采用上文中介绍的一维情况的解决方法求解,若此时c不是一维的,则初始化一个空集 I I I,可以提前用Fisher-Yates算法对H的序列进行打乱,打乱后进行for循环时,每次依次从H中取一个h,然后判断:
情况1:若当前最优解属于h,则当前最优解满足约束h,不需要计算新的最优解,直接将h添加到集合 I I I中,继续进行下一轮for循环,处理下一个约束h
情况2:若当前的最优解不属于h,则需要计算一个新的最优解x,将已经加入到集合 I I I中的约束用高斯消元法投影到约束h的边界上,得到低一个维度的H’,然后将c也用高斯消元法投影到h上,得到低一个维度的c’,然后将低一个维度的H’和c’作为参数递归调用SeidelLP()函数本身进行降维处理,直至降为1维情况。然后就可以得到新的最优解x,此时约束h已经满足,将其添加到集合 I I I中,本轮循环结束,继续进行下一轮for循环,处理下一个约束h。
for循环结束后,即可得到满足所有约束hi的最优解x
当d的维数较大时,比如d是20维的,深层次的递归调用可能出现复杂度爆炸,但当d的维数是个位数时,可以高效率的得到精确解。
接下来借助下图中的例子,来看一下如何使用高斯消元法将d维的半空间,投影成d-1维的半空间:
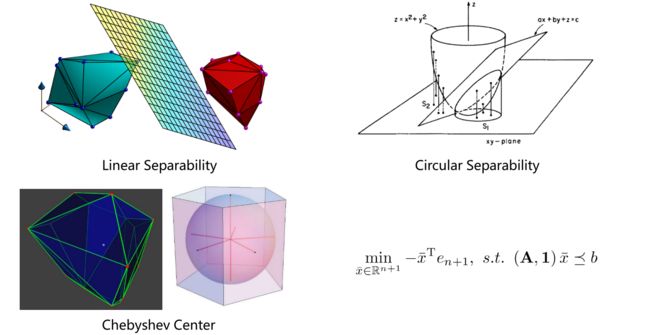
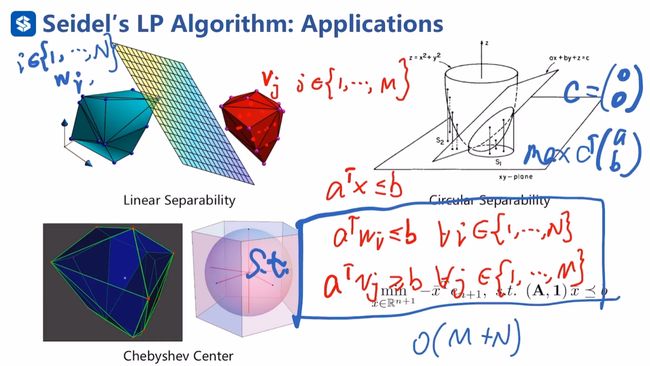
Seidel′s LP线性规划可以高效的处理维度不高,约束很多的情况,可以得到高效率的精确解。下图给出了一些应用实例
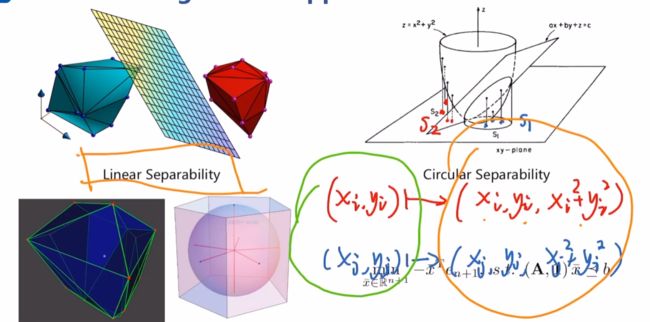
(1)线性可分问题:假设图中红色凸多边形是障碍物,蓝色凸多边形是机器人或机器人的一部分,现在想要知道机器人是否与障碍物发生了碰撞,可以将障碍物的顶点及其内部的一些冗余点vi与机器人的顶点及其内部的一些冗余点wi,若他们不碰撞,那必然存在一个分离超平面,设该超平面为 a T x < = b a^\mathrm{T}x<=b aTx<=b,则机器人满足 a T w i < = b a^\mathrm{T}w_{i}<=b aTwi<=b,障碍物满足 a T v i > = b a^\mathrm{T}v_{i}>=b aTvi>=b,在这两组约束下,求解目标函数 c T x c^\mathrm{T}x cTx,这里的x即为a,b构成的向量,c可设成0向量。可求得任意一个可行超平面,说明两者没有碰撞。Seidel′s LP线性规划可以很好的用于检测机器人是否与障碍物发生了碰撞。
(2)圆形可分问题,在工业流水线的机器视觉中有时需要判断是否存在一个圆来分隔两种点集,如下图中的蓝色点集和红色点集
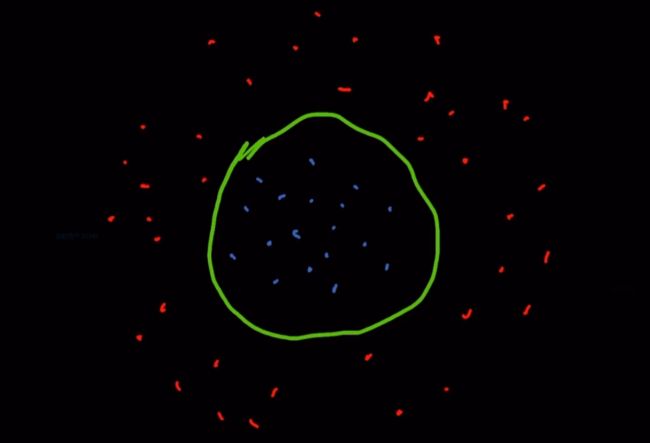
可以进行升维处理,将圆形区域作为增加的维度,下图等式中右侧是一个线性可分问题,若右侧表达式线性可分,则左侧表达式存在圆形来分隔两个点集
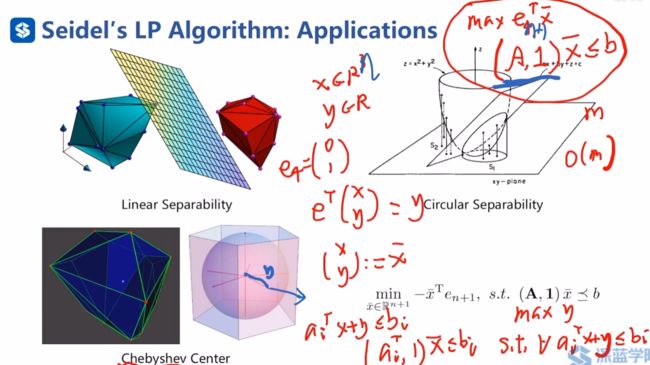
(3)在安全区域中找一个点,距离安全区域的边界的距离最大化,即在安全区域中找一个圆,使得该圆的半径最大化,即最小的碰撞距离最大化,此时圆心即为所求的最安全的点。
参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化