一文讲解Transformer
我们本篇文章来详细讲解Transformer:
首次提出在:Attention is all you need (arxiv.org)
简单来说,Transfomer就是一种Seq2seq结构,它基于多头自注意力机制,解决了传统RNN在计算过程中不能够并行化的问题。即相较于RNN而言,Transfomer所采用的多头自注意力机制更快,因为,对于每个单词(即被分割的每个单位),它可以并行计算。而不是向传统RNN那样,必须要在前面的单词(特征)计算出来之后,才可以对后面的单词(特征)进行计算。
对于Transformer的整体结构而言,它可以分成两块,即Encoder和Decoder,分别是编码器和解码器部分。在这两部分中,均采用了多头自注意力机制这样一个组件。
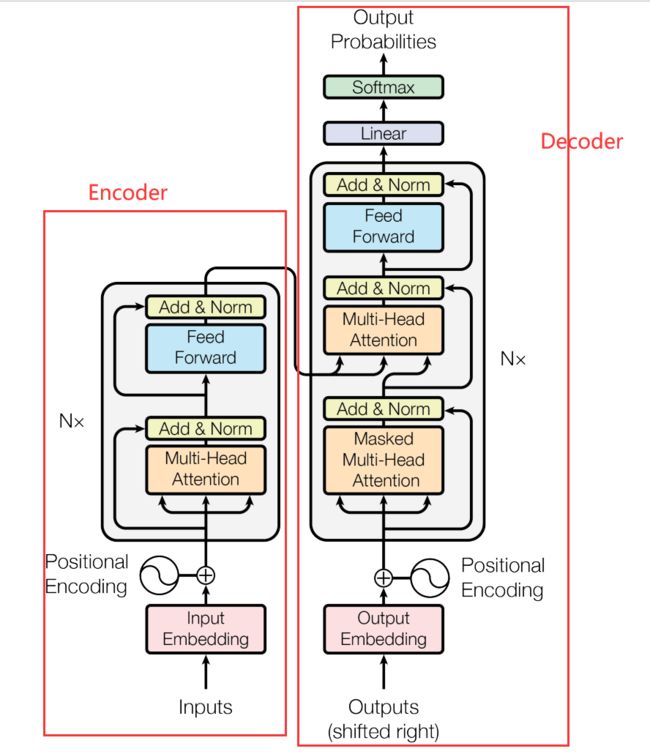
如上图所示,左侧为Encoder,右侧为Decoder。
在Encoder中,先将inputs进行input Embedding(单词编码,可以有很多种方式,例如可以采用 Word2Vec、Glove 等算法预训练得到,也可以在 Transformer 中训练得到)。
紧接着进行位置编码(Positional Encoding),它的目的是为了防止该模型结构变成了一个词袋模型。因为从后面的介绍将会看出,自注意力机制所计算出来的结果是和位置无关的。具体来说,将输入的向量a加上一个向量e,也即位置编码。这个e是认为计算出来的。通常采用正弦位置编码方案。
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d ) PE_{(pos,2i)}=sin(pos/10000^{2i/d}) PE(pos,2i)=sin(pos/100002i/d)
P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d ) PE_{(pos,2i+1)}=cos(pos/10000^{2i/d}) PE(pos,2i+1)=cos(pos/100002i/d)
其中,pos表示单词在句子中的位置,d表示PE的维度,其中2i表示偶数维度,2i+1表示奇数维度。
这样做的好处(即算出来,而不是train出来的好处):
1、使 PE 能够适应比训练集里面所有句子更长的句子,假设训练集里面最长的句子是有 20 个单词,突然来了一个长度为 21 的句子,则使用公式计算的方法可以计算出第 21 位的 Embedding。
2、可以让模型容易地计算出相对位置,对于固定长度的间距 k,PE(pos+k) 可以用 PE(pos) 计算得到。因为 Sin(A+B) = Sin(A)Cos(B) + Cos(A)Sin(B), Cos(A+B) = Cos(A)Cos(B) - Sin(A)Sin(B)。(中学时三角函数变换计算)
至于为什么是相加,解释起来有点复杂:
假设我不是加上去的,因为这样多多少少有些突兀,我是拼接上去的。也即,我把能够代表位置的向量拼接到原本的input Embedding中。
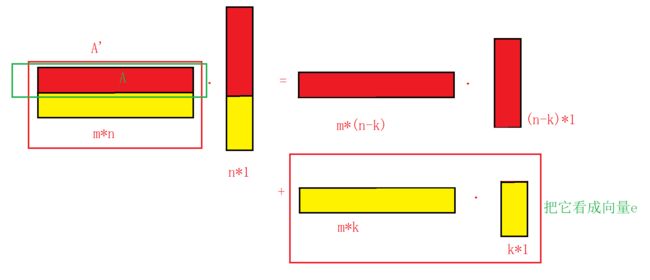
在input Embedding时,会乘以一个矩阵来进行编码变换的。我们设该矩阵为A,原本的单词向量我们设置为a,那么得到的就是 W = A T ⋅ a W = A^{T}·a W=AT⋅a
接着,如果我要是拼上去的,那么我假设我需要用的矩阵就是A’ ,那么 W ′ = A ′ T ⋅ a W' = A'^{T}·a W′=A′T⋅a。如下图所示:
接下里,我们介绍多头自注意力机制。在此之前,我们先来介绍自注意力机制。
在传统的RNN当中,由于它存在无法并发执行、梯度丢失等问题。如果我们考虑CNN来去解决这类问题,但是想要用CNN来去解决又往往需要叠很多的卷积层。也不很合适。于是,就有人提出了一种基于自注意力机制的组件,来去解决这类问题。它可以做到,通过注意力机制,关联句子中长距离的语义关系,而且,Self-Attention可以比RNN更好地解决长时依赖问题。因为它的计算量比RNN低,它可以进行并行计算。
具体来说,自注意力机制可以这样解释:
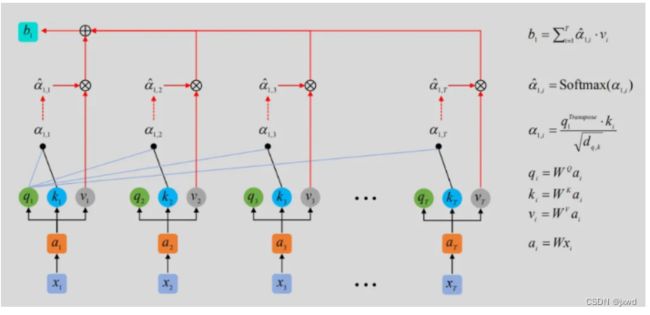
如上图。对于输入的单词向量 x 1 x_1 x1… x n x_n xn,经过单词编码和位置编码,得到 a 1 a_1 a1… a n a_n an。
然后,我们要得到三个不同的向量。分别成为query(q)、key(k)和value(v),其中,q和k是用来计算关联程度的,而v是用来进行关联度查询。这三个向量的得到,是由 a a a分别乘以 W Q W^Q WQ、 W K W^K WK、 W v W^v Wv得到。
也就是说,所有的 q q q,即 q 1 、 q 2 . . . q r q_1、q_2...q_r q1、q2...qr,是由 a 1 、 a 2 . . . a r a_1、a_2...a_r a1、a2...ar乘以 W Q W^Q WQ得到,
同理,所有的 k k k,即 k 1 、 k 2 . . . k r k_1、k_2...k_r k1、k2...kr,是由 a 1 、 a 2 . . . a r a_1、a_2...a_r a1、a2...ar乘以 W K W^K WK得到,
所有的 v v v,即 v 1 、 v 2 . . . v r v_1、v_2...v_r v1、v2...vr,是由 a 1 、 a 2 . . . a r a_1、a_2...a_r a1、a2...ar乘以 W V W^V WV得到。
接下来,计算q和k的Attention。即他们关联由多大。计算公式为 a i , j = q i T ⋅ k j d q , k a_{i,j} = \frac{q^{T}_{i}·k_{j}}{\sqrt{d_{q,k}}} ai,j=dq,kqiT⋅kj,这里的d表示的是q、k的维数。需要注意的是,是每一个 q q q,和每一个 k k k都要计算。
以上图为例, q 1 q1 q1和 k 1 k1 k1,那么得到的就是 a 1 , 1 = q 1 T ⋅ k 1 d q , k a_{1,1} = \frac{q^{T}_{1}·k_{1}}{\sqrt{d_{q,k}}} a1,1=dq,kq1T⋅k1,我们将结果记为 a 1 , 1 a_{1,1} a1,1,与此同时,按照同样的方法,得到 a 1 , 2 、 a 1 , 3 a_{1,2}、a_{1,3} a1,2、a1,3…
接着,再将所有的 a a a进行softmax函数操作。所谓softmax,和sigmod类似。函数表达式: s o f t m a x ( x ) = e x i ∑ j = 1 n e x j {softmax(x)=\frac{e^{x_i}}{\sum_{j=1}^n{e^{x^j}}}} softmax(x)=∑j=1nexjexi它的作用是求每一部分的概率,映射到同一区域内(输出为互斥类别,且只能选择一个类别)。这样以后,就得到 a ^ 1 , j {\hat{a}_{1,j}} a^1,j
最后,将 a 1 , j ( s o f t m a x 后的 ) a_{1,j}(softmax后的) a1,j(softmax后的)分别和 v j v_j vj相乘,然后求和,就得到 b 1 b_1 b1,
同理,将 a 2 , j ( s o f t m a x 后的 ) a_{2,j}(softmax后的) a2,j(softmax后的)分别和 v j v_j vj相乘,然后求和,就得到 b 2 b_2 b2,
…
直至全部输出 b 1 . . . b n b_1 ... b_n b1...bn,
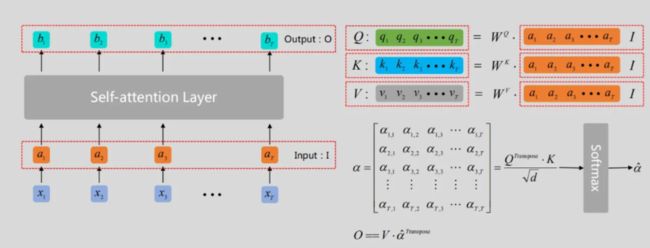
不过,与RNN相比较,可以看到,我们的transformer在计算到 b 1 . . . b n b_1 ... b_n b1...bn时,是可以同步的。因为它可以通过一个矩阵,来一次性全部计算完。如下图(右侧公式):
在这样一个组件中,我们每一个 b b b的得到,和输入的每个 a a a都是相关的。所以,我们就可以通过学习,得到某些单词之间的相关性应该是高还是低。即便两个单词相距很远,但仍可以察觉到关联。因为在整个注意力机制中,它和位置是无关的。“天涯若比邻”。
这就是自注意力机制。
我们下面来介绍多头自注意力机制。
所谓多头,就是同时有多个自注意力机制。每个注意力机制中,所关注的关联有一定区别,从而,在训练过程中,可以充分考虑不同单词之间的关联程度,从而可以很好地实现泛化。
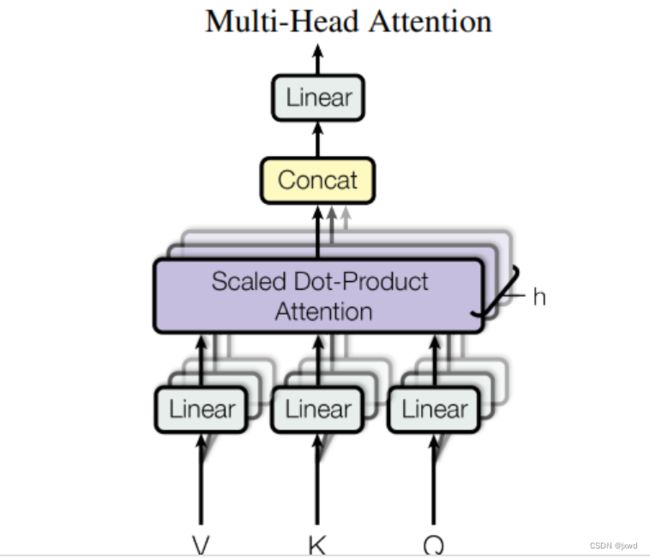
那多头注意力机制,是怎么训练的呢?答:和单个的自注意力机制一模一样。在Transformer模型中,一共用到了8个头。这样,一组输入通过八个自注意力机制,就得到了八个输出矩阵。然后,我们将这八个矩阵Contact(拼接)在一起,然后进行一个Liner变换,最终得到一个n×n的矩阵。具体过程如下图所示:
(原论文中的图,在此图中,直观地展示了多头自注意力的运转过程)
下图中,展示了具体过程:
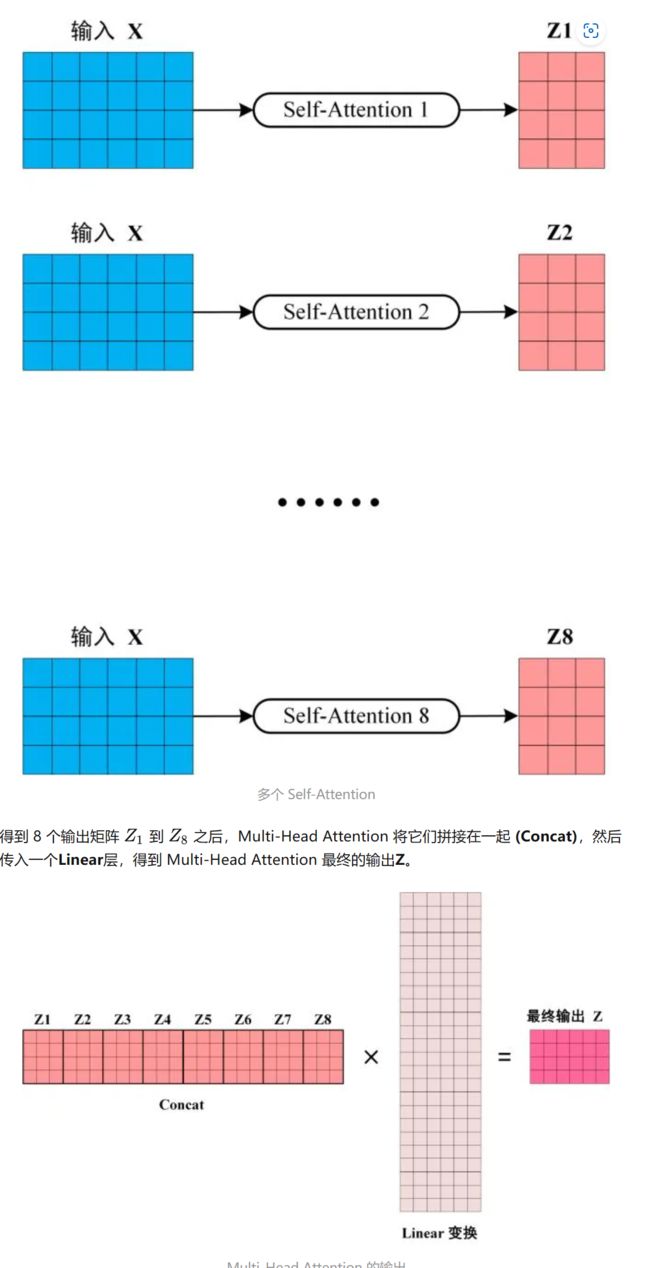
多头自注意力机制到此介绍完毕。接下来继续介绍Transformer。
左侧,Encoder部分,经过了Multi-Head Attention后,得到的输出,和Multi-Head Attention的输入,进行Add&Norm,即残差连接加归一化(标准化)。
残差连接刚刚已说过,就是X(输入) + Multi-Head-Attention)(X)->输入加输出的方式,让其可以更好地只关注差异。
Norm这里指归一化,所使用的是 Layer Normalization,将每一层神经元的输入都转成均值方差都一样的,用来加快收敛。注意,这里的每一层,而不是每一个维度(每一个维度是Batch Normalization)。所采用的归一化公式是z-score归一化。因为样本范围不确定。
进行Add&Norm之后,进行Feed Forward运算。Feed Forward实际上很简单,是一个两层的全连接层,第一层的激活函数为 Relu,第二层不使用激活函数。因此,它的公式为: m a x ( 0 , X W 1 + b 1 ) W 2 + b 2 max(0,XW_1+b_1)W_2+b_2 max(0,XW1+b1)W2+b2
X是输入,Feed Forward 最终得到的输出矩阵的维度与X一致。
然后继续进行Add&Norm。
这样以后,算是经过了一个Encoder Block。通过多个 Encoder block 叠加就可以组成 Encoder(Transformer用到了N个)。
第一个 Encoder block 的输入为句子单词的表示向量矩阵,后续 Encoder block 的输入是前一个 Encoder block 的输出,最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C,这一矩阵后续会用到 Decoder 中。
到此为止,Encoder解释完毕。
接下来看Decoder。我们先来看右下角的Masked Multi-Head Attention
需要明白,在Decoder中,需要根据之前的翻译,来去找到当前最可能的翻译。没有被翻译出来的内容不能被看到。
所以,这里引入了一个Masked自注意力机制。它的输入是已经输出出来的单词(因为需要根据之前的翻译来去推测之后的翻译)。而在最一开始的时候,是一个类似于标志位的东西。所谓Masked,就是对矩阵进行遮挡。把不知道的部分变成0。
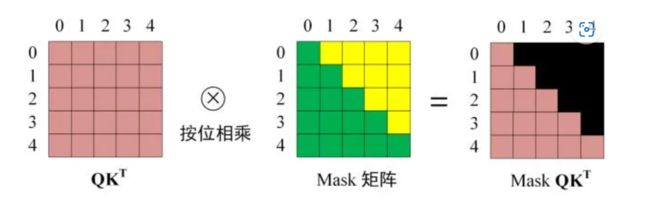
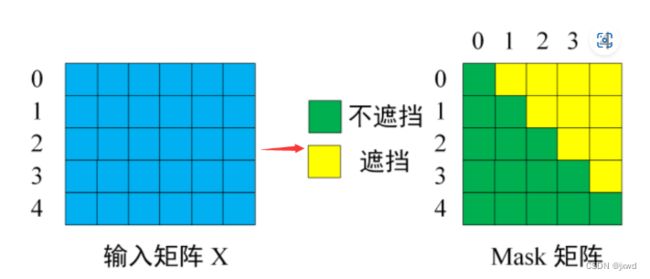
如下图,对于原本的输入矩阵,在 Mask 可以发现单词 0 只能使用单词 0 的信息,而单词 1 可以使用单词 0, 1 的信息,即只能使用之前的信息。
注意,这里的Masked矩阵,在训练当中,由于我们已经提前知道了其正确答案,所以遮挡住有其必要性。否则拿未预测出的部分去预测自己,就相当于作弊了。
而在预测时,我们实际上本身就不知道后面的内容到底是什么。即便我们不遮挡,我们也是不知道后面是什么的——但换一种理解方式,就好似后面的内容被遮挡住了,所以我们看不见。
确定了输入矩阵之后,接下来的操作就和之前的self-Attention一样了。通过输入矩阵X,来去计算Q、K、V。然后计算Q和K的Attention score,然后再用Mask矩阵进行遮挡。遮挡操作如图:
得到Mask Q K T QK^T QKT之后,再去进行softmax,然后和V相乘,然后再关联、做Liner变换、求和。
Masked Multi-Head Attention介绍完毕。
然后看上面的Multi-Head Attention部分。
Decoder block 第二个 Multi-Head Attention 变化不大, 主要的区别在于其中 Self-Attention 的 K, V矩阵不是使用 上一个 Decoder block 的输出计算的,而是使用 Encoder 的编码信息矩阵 C 计算的。
根据 Encoder 的输出 C计算得到 K, V,根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个 Decoder block 则使用输入矩阵 X 进行计算),后续的计算方法与之前描述的一致。
这样做的好处是在 Decoder 的时候,每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。
这样,就能构成一个Decoder block。
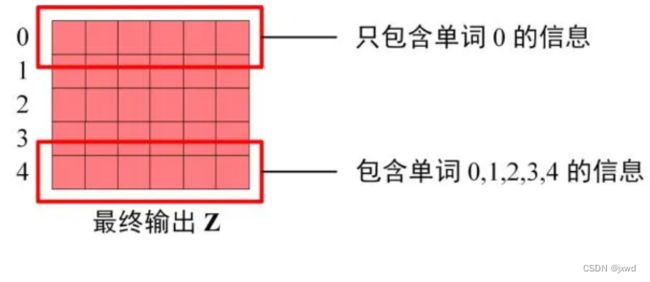
Decoder block 最后的部分是利用 Softmax 预测下一个单词,在之前的网络层我们可以得到一个最终的输出 Z,因为 Mask 的存在,使得单词 0 的输出 Z0 只包含单词 0 的信息,如下:
与Encoder一样,Decoder也是由N个Decoder block组成(就是多个)
Transformer介绍到这里基本结束。
参考:
1、Transformer模型详解(图解最完整版) - 知乎 (zhihu.com)
2、1706.03762.pdf (arxiv.org)
3、Multi-headed Self-attention(多头自注意力)机制介绍 - 知乎 (zhihu.com)
4、Transformer,BERT模型介绍 - 知乎 (zhihu.com)
5、Transformer - YouTube