- 使用LangChain访问个人数据第一章-简介
明志刘明
大模型学习手册langchain
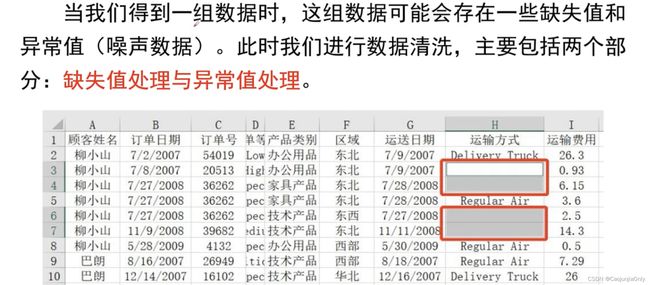
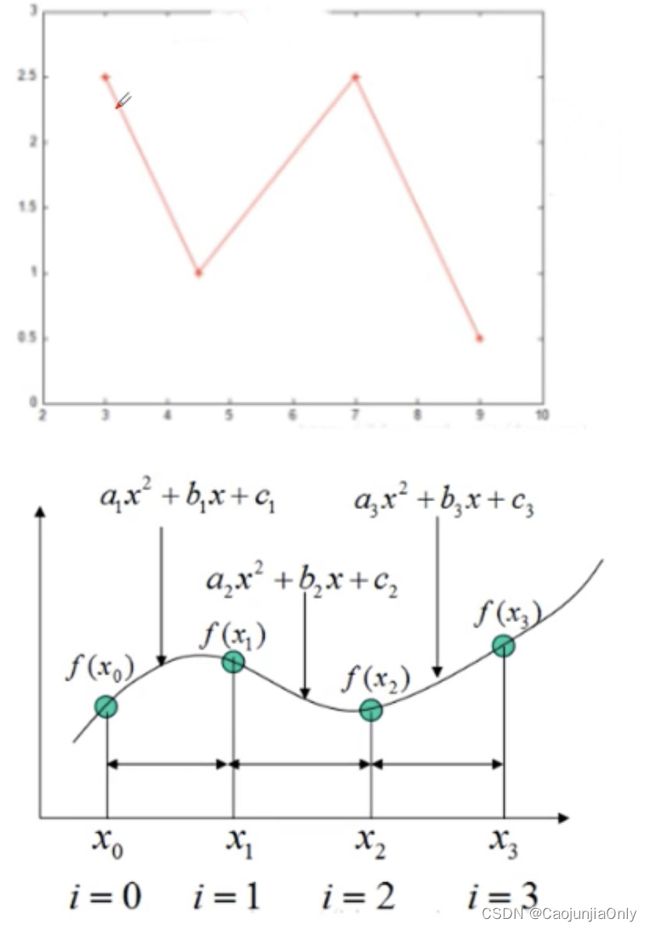
需要学习提示词工程的同学请看面向开发者的提示词工程需要学习ChatGPT的同学请查看搭建基于ChatGPT的问答系统需要学习LangChian开发的同学请查看基于LangChain开发应用程序正文在大数据时代,数据价值逐渐凸显,打造定制化、个性化服务,个人数据尤为重要。要开发一个具备较强服务能力、能够充分展现个性化智能的应用程序,大模型与个人数据的对齐是一个重要步骤。作为针对大模型开发应运而生的框
- 探索R语言:经典案例解析与源代码
翠绿探寻
r语言信息可视化开发语言R语言
探索R语言:经典案例解析与源代码引言:R语言是一种流行的数据分析和统计建模工具,具有丰富的功能和广泛的应用领域。在本文中,我们将通过经典案例来探索R语言的一些重要功能和技术。我们将提供相应的源代码,以便读者能够实际运行并理解这些示例。案例一:数据导入与处理在数据分析中,数据导入和处理是首要任务。R语言提供了丰富的函数和包,用于处理各种数据格式。下面是一个简单的示例,演示了如何导入和处理CSV格式的
- 数据分析与AI丨AI Fabric:数据和人工智能架构的未来
Altair澳汰尔
数据分析aiRapidMiner知识图谱人工智能
AIFabric架构是模块化、可扩展且面向未来的,是现代商业环境中企业实现卓越的关键。在当今商业环境中,数据分析和人工智能领域发展可谓日新月异。几乎每天都有新兴技术诞生,新的应用场景不断涌现,前沿探索持续拓展。可遗憾的是,众多企业在利用数据和人工智能方面,脚步总是滞后。这是每个行业进行创新和获得竞争优势的冲刺阶段,但正如大多数企业时常感受到的那样,大规模实施下一代数据和AI工具说起来容易做起来难。
- Linux下安装Mysql环境
软件分享工作室
Linuxlinuxmysql运维
1.mysql说明MySQL是一种开源的关系型数据库管理系统,它具有高性能、可靠性和灵活性的特点。MySQL支持多种操作系统,包括Windows、Linux和MacOS等。它是最流行的数据库管理系统之一,被广泛应用于网站开发、数据存储和数据分析等领域。2.mysql优点1.开源免费:MySQL是开源软件,可以免费使用和修改,没有任何使用限制。2.跨平台:MySQL可以在多种操作系统上运行,包括Wi
- Python学习指南:系统化路径 + 避坑建议
程之编
Python全栈通关秘籍青少年编程python开发语言人工智能机器学习
新手小白学习编程就像搭积木——需要从基础开始,逐步构建知识体系。以下是为你量身定制的Python学习路径,帮你告别杂乱,高效入门!一、学习前的关键认知明确目标:想用Python做什么?数据分析(如Excel自动化、可视化)Web开发(如搭建网站)人工智能(如机器学习)自动化办公(如处理文件、邮件)目标不同,后续学习侧重点不同(但基础通用)。避免误区:❌只看教程不写代码✅边学边动手,哪怕抄代码也要运
- 架构生命周期(演进史)技术应服务于业务
Limbo1213
java架构生命周期演进史
架构生命周期简介本篇幅主要讲述架构的各阶段出现的需求问题、业务问题、性能问题以及相应的解决方案。1、web1.0时代(1996年左右)2、web2.0时代(2006年左右)3、互联网时代(2012年左右)–》互联网±-》智慧城市。滴滴打车。饿了么(工商局)4、大数据+云计算5、AI未来以来时代…第一时期单一应用架构allinone。所有的模块和代码都在一起。技术也不分层。(2000年左右)网站的初
- MySQL-关于如何保存“大数据”
赵师的工作日
mysql大数据数据库
作者:赵师的工作日(赵明中)现役OracleACE、MySQL8.0ocp、TiDBPCTA\PCTP、ElasticsearchCertifiedEngineer微信号:mzzhao23微信公众号:赵师的工作日墨天轮社区:赵师的工作日CSND:赵师的工作日数据库的种类有很多,各类数据库充分发挥各自的优势从而保证业务稳定运行,mysql轻量级、关键数据,redis缓存、快,ES搜索,Mongodb
- ClickHouse 作用,优缺点。
mldsh13
clickhouse
ClickHouseClickHouse是一个开源的分布式列式数据库管理系统(DBMS),专门设计用于实时分析(OLAP)。它最初由俄罗斯的Yandex开发,后来成为了开源项目,被广泛应用于需要高性能数据分析和查询的场景。作用:实时分析:ClickHouse专注于快速查询和分析大量数据,使其特别适用于数据分析、报告和实时仪表板等应用场景。大规模数据处理:能够处理海量数据,支持分布式架构,可以水平扩
- PIPCA个人信息保护合规审计师认证介绍!
熙丫 13381482386
大数据
个人信息保护合规审计师"(PersonalInformationProtectionComplianceAuditor-CCRC)是中国网络安全审查认证中心与市场监管大数据中心为深入贯彻实施《个人信息保护法》,推动个人信息处理者切实履行合规审计职责,针对企事业单位及第三方机构中从事个人信息保护合规审计(简称“个保审计”)的专业人员,依据《个人信息保护法》、《网络安全从业人员能力基本要求》
- doris:阿里云 MaxCompute
向阳1218
大数据doris
MaxCompute是阿里云上的企业级SaaS(SoftwareasaService)模式云数据仓库。什么是MaxCompute连接MaxCompute示例--1.创建Catalog。CREATECATALOGmcPROPERTIES("type"="max_compute","mc.default.project"="xxx","mc.access_key"="xxxx","mc.secret_
- Apache Doris 实现毫秒级查询响应
随风九天
匠心数据库服务javaapacheApacheDoris
1.引言1.1数据分析的重要性随着大数据时代的到来,企业对实时数据分析的需求日益增长。快速、准确地获取数据洞察成为企业在竞争中脱颖而出的关键。传统的数据库系统在处理大规模数据时往往面临性能瓶颈,难以满足实时分析的需求。例如,一个电商公司需要实时监控销售数据以调整库存和营销策略,而传统的数据库可能需要数分钟甚至数小时才能生成报表,这显然无法满足业务需求。1.2ApacheDoris简介ApacheD
- JSON数据解析实战:从嵌套结构到结构化表格
亿牛云爬虫专家
代理IP爬虫代理pythonjson数据解析嵌套结构结构化表格GoogleScholar学术文献爬虫代理
在信息爆炸的时代,如何从杂乱无章的数据中还原出精准的知识图谱,是数据侦探们常常面临的挑战。本文以GoogleScholar为目标,深入解析嵌套JSON数据,从海量文献信息中提取关键词、作者、期刊等内容。最终,我们不仅将数据转换成结构化表格,还通过Graphviz制作出技术关系图谱,揭示文献间的隐秘联系。关键数据分析在本次调研中,我们的核心目标是获取GoogleScholar上的学术文献信息。为此,
- ClickHouse Keeper 源码解析
阿里云云栖号
云栖号技术分享java开发语言后端
简介:ClickHouse社区在21.8版本中引入了ClickHouseKeeper。ClickHouseKeeper是完全兼容Zookeeper协议的分布式协调服务。本文对开源版本ClickHousev21.8.10.19-lts源码进行了解析。作者简介:范振(花名辰繁),阿里云开源大数据-OLAP方向负责人。内容框架背景架构图核心流程图梳理内部代码流程梳理Nuraft关键配置排坑结论关于我们R
- 基于大数据架构的就业岗位推荐系统的设计与实现【java或python】—计算机毕业设计源码+LW文档
qq_375279829
大数据架构python课程设计算法
摘要随着互联网技术的迅猛发展和大数据时代的到来,就业市场日益复杂多变,求职者与招聘方之间的信息不对称问题愈发突出。为解决这一难题,本文设计并实现了一个基于大数据架构的就业岗位推荐系统。该系统通过收集、整合并分析大量求职者简历信息、企业招聘信息以及市场动态数据,运用先进的机器学习算法,为求职者提供个性化的岗位推荐服务,同时帮助企业快速定位到合适的候选人。本文将从系统设计的背景与意义、技术基础、需求分
- 供应链工作效率如何提升
dev.null
社会供应链
提升供应链工作效率可以从以下几个关键方面入手:1.优化供应链管理数据驱动决策:利用AI和大数据分析,提高预测准确性,优化库存管理。供应链可视化:采用ERP(企业资源计划)和SCM(供应链管理)系统,实现实时跟踪和监控。流程自动化:使用RPA(机器人流程自动化)减少人为操作,提高效率。2.提高物流效率智能调度:使用AI优化配送路线,减少运输时间和成本。自动化仓储:采用自动分拣、机器人搬运、无人机配送
- 使用Activeloop Deep Lake构建深度学习数据仓库与向量存储
dgay_hua
深度学习人工智能python
技术背景介绍随着深度学习技术的发展,数据的存储与管理成为了一个重要的问题。尤其是对于需要处理大量数据的应用,例如自然语言处理和图像识别,传统的数据存储方式已经无法满足需求。ActiveloopDeepLake是专为深度学习设计的数据仓库,可以作为向量存储使用,支持多模态数据的存储和处理,并且可以直接用于细调大型语言模型(LLMs)。此外,它还提供自动版本控制,无需依赖其他服务,兼容主要云服务提供商
- 【PyCharm】Python和PyCharm的相互关系和使用联动介绍
lisw05
pythonpythonpycharmide
李升伟整理Python是一种广泛使用的编程语言,而PyCharm是JetBrains开发的专门用于Python开发的集成开发环境(IDE)。以下是它们的相互关系和使用联动的介绍:1.Python和PyCharm的关系Python:一种解释型、面向对象的高级编程语言,适用于多种开发任务,如Web开发、数据分析、人工智能等。PyCharm:专为Python设计的IDE,提供代码编辑、调试、测试、版本控
- 【人工智能】农业工程与信息技术文献推荐
lisw05
人工智能农业信息技术机器人
李升伟整理1.农业物联网与智能化管理《农业物联网导论》作者:李道亮内容简介:本书系统介绍了农业物联网的基本概念、技术架构及其在农业生产中的应用,包括传感器网络、远程监控、智能决策支持系统等。《农业信息智能获取技术》作者:岳峻、傅泽田、高文内容简介:重点探讨了如何利用信息技术获取农业数据,包括遥感技术、无人机监测和传感器网络的应用。2.农业大数据与决策支持《农业大数据:理论与实践》作者:梅方权内容简
- phoenix无法连接hbase shell创建表失败_报错_PleaseHoldException: Master is initializing---记录020_大数据工作笔记0180
添柴程序猿
hbase连接报错phoenix连接hbasephoenixPleaseHoldExcep
今天发现,我的phoenix,去连接hbase集群,怎么也连不上了,奇怪了...弄了一晚上org.apache.hadoop.hbase.PleaseHoldException:Masterisinitializing[root@hadoop120bin]#ll总用量184-rwxr-xr-x.1rootroot36371月222020chaos-daemon.sh-rwxr-xr-x.1root
- 数据分析在宇宙观测中的重要性
AI天才研究院
计算ChatGPTDeepSeekR1&大数据AI人工智能大模型javapythonjavascriptkotlingolang架构人工智能大厂程序员硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLM系统架构设计软件哲学Agent程序员实现财富自由
数据分析在宇宙观测中的重要性关键词:数据分析、宇宙观测、数据预处理、数据挖掘、数据可视化摘要:本文将探讨数据分析在宇宙观测中的重要性,从数据分析在宇宙观测中的应用背景、重要性、面临的挑战与机遇以及未来发展趋势等方面进行深入分析,旨在为读者提供一个全面而详细的了解。引言第1章:分析数据与宇宙观测的关联1.1.1数据分析在宇宙观测中的应用背景宇宙观测是研究宇宙的结构、演化、性质以及各种物理现象的科学。
- 物联网-电路局“一杆一档”管理
小赖同学啊
智能硬件物联网
电路局“一杆一档”管理及设备管理维修的技术实现为了实现电路局对电杆及其安装设备的“一杆一档”管理,并结合设备管理、维修等相关工作,可以通过物联网(IoT)、地理信息系统(GIS)、大数据、人工智能(AI)和移动互联网等技术手段,构建一个智能化、数字化的管理系统。以下是详细的技术实现方案。1.实现目标“一杆一档”管理:为每根电杆建立唯一的数字化档案,记录其位置、型号、安装时间、维护记录等信息。对电杆
- 淘宝天猫商品评论数据接口:实时API调用指南
pythonc++java
淘宝天猫商品评论数据接口是用于获取淘宝和天猫平台上商品评论数据的工具。通过该接口,开发者可以实时调用API获取所需数据,为数据分析、应用开发等提供便利。以下是淘宝天猫商品评论数据接口的实时API调用指南:一、准备工作注册淘宝开放平台账号:访问淘宝开放平台官网,注册并登录账号。申请API密钥:在开放平台中,申请API密钥,以便在调用接口时进行身份验证。熟悉API文档:仔细阅读淘宝开放平台的API文档
- 基于SpringBoot的智能问诊系统设计与隐私保护策略
大熊计算机
技术博文springboot后端java
通过SpringBoot框架,我们可以快速搭建一个智能问诊系统,为用户提供便捷的线上医疗服务。然而,在系统设计和实现过程中,如何保障用户的隐私和数据安全,始终是一个亟需关注的问题。本文将探讨基于SpringBoot的智能问诊系统的设计原理、开发实践及隐私保护策略。1.智能问诊系统概述智能问诊系统是基于人工智能、数据分析及信息技术等手段,通过网络平台为用户提供医疗咨询、初步诊断、健康管理等服务的系统
- 2025最新Linux系统深度优化指南:20个核心技巧与实战案例解析
emmm形成中
linux应用实操服务器linuxgithub
2025最新Linux系统深度优化指南:20个核心技巧与实战案例解析摘要:随着Linux在云计算、大数据、AI等领域的广泛应用,系统性能优化成为运维工程师的核心技能。本文结合2025年最新实践案例,从内核调优、资源管理、安全加固到云原生适配,全面解析Linux系统优化的20项核心技术,助力企业打造高性能、高可用的服务器环境。一、Linux系统优化的重要性与趋势在数字化转型加速的背景下,Linux系
- python数据分析一周速成2.连表查询【含数据库实战项目】
噼里啪啦噼酷啪Q
数据分析数据分析CDApython
连表查询结合数据库实战(sql和hive跨库取数)数据准备#前面省略数据库连接,提示:可以用pymysql和pyhive模块pre_sql="""selectap,timefrombiaoyiawherea.time>20250101"""sql_df=run_mysql(pre_sql)pre_hive="""selectapplication_number,activation_dtefrom
- 数学建模与优化算法在确定X和Y值时,如何处理实验数据的不确定性?
学术乙方
油纸绝缘算法经验分享
在数学建模与优化算法中处理实验数据的不确定性以确定油纸绝缘系统中的X和Y值,可以参考以下方法和步骤:建立数学模型油纸绝缘系统的几何结构可以用X-Y模型来描述,其中X表示挡板厚度与总厚度的比值,Y表示间隔器宽度与总宽度的比值。这些参数直接影响油纸绝缘的介电特性。通过实验数据(如介电谱曲线)和理论模型,可以建立数学方程来描述X和Y对介电特性的影响。引入不确定性建模实验数据通常存在测量误差、环境变化等因
- 大数据与hdfs创建文件夹
猫猫头有亿点炸
大数据hdfshadoop
注意事项:在hdfs上操作的文件,创建文件的时候注意他与linux是不一样的(模式如下:)hdfsdfs-mkdir/test1错误示例:否则,无论如何hdfsdfs-ls/test1/都没有文件的
- 【基础5】归并排序
流光听风语
基础算法排序算法算法
核心思路归并排序基本思想是将一个数组分成两个子数组,分别对这两个子数组进行排序,然后将排好序的子数组合并成一个最终的有序数组,即分治法:分:将数组递归拆分成左右两半,直到每个子数组只剩1个元素(天然有序)。治:将两个有序子数组合并为一个有序数组,直到合并成完整数组。优缺点优点缺点✅稳定排序(相等元素顺序不变)❌额外空间(需O(n)临时数组)✅时间复杂度稳定O(nlogn)❌递归可能栈溢出(极大数据
- web组态可视化平台
万维——组态
物联网编辑器数学建模前端低代码
Web组态可视化软件是一种用于创建、管理和展示工业自动化、物联网(IoT)和智能建筑等领域的图形化界面的工具。它允许用户通过Web浏览器实时监控和控制设备、系统或流程。以下是几款常见的Web组态可视化软件:1.ThingsBoard特点:开源、支持物联网设备管理、数据可视化、报警管理。适用场景:物联网平台、设备监控、数据分析。优势:高度可定制化,支持多种协议(MQTT、CoAP、HTTP等)。2.
- 智能遥感新质生产力:ChatGPT、Python和OpenCV强强联合;空天地遥感数据分析的全流程;地面数据、无人机数据、卫星数据、多源数据等处理
小艳加油
DeepSeekChatGPT遥感遥感新质生产力ChatGPTOpenCV遥感数据处理
通过系统化的模块设计和丰富的实战案例,深入理解和掌握遥感数据的处理与计算。不仅涵盖了从零基础入门Python编程、OpenCV视觉处理的基础知识,还将借助ChatGPT智能支持,引导您掌握遥感影像识别和分析的进阶技术。更为重要的是,通过15个经过精心设计的真实案例,深度参与地质监测、城市规划、农业分析、生态评估等不同场景下的遥感应用实践。层层递进、结构严谨,帮助您系统性掌握从数据预处理、图像增强、
- mondb入手
木zi_鸣
mongodb
windows 启动mongodb 编写bat文件,
mongod --dbpath D:\software\MongoDBDATA
mongod --help 查询各种配置
配置在mongob
打开批处理,即可启动,27017原生端口,shell操作监控端口 扩展28017,web端操作端口
启动配置文件配置,
数据更灵活
- 大型高并发高负载网站的系统架构
bijian1013
高并发负载均衡
扩展Web应用程序
一.概念
简单的来说,如果一个系统可扩展,那么你可以通过扩展来提供系统的性能。这代表着系统能够容纳更高的负载、更大的数据集,并且系统是可维护的。扩展和语言、某项具体的技术都是无关的。扩展可以分为两种:
1.
- DISPLAY变量和xhost(原创)
czmmiao
display
DISPLAY
在Linux/Unix类操作系统上, DISPLAY用来设置将图形显示到何处. 直接登陆图形界面或者登陆命令行界面后使用startx启动图形, DISPLAY环境变量将自动设置为:0:0, 此时可以打开终端, 输出图形程序的名称(比如xclock)来启动程序, 图形将显示在本地窗口上, 在终端上输入printenv查看当前环境变量, 输出结果中有如下内容:DISPLAY=:0.0
- 获取B/S客户端IP
周凡杨
java编程jspWeb浏览器
最近想写个B/S架构的聊天系统,因为以前做过C/S架构的QQ聊天系统,所以对于Socket通信编程只是一个巩固。对于C/S架构的聊天系统,由于存在客户端Java应用,所以直接在代码中获取客户端的IP,应用的方法为:
String ip = InetAddress.getLocalHost().getHostAddress();
然而对于WEB
- 浅谈类和对象
朱辉辉33
编程
类是对一类事物的总称,对象是描述一个物体的特征,类是对象的抽象。简单来说,类是抽象的,不占用内存,对象是具体的,
占用存储空间。
类是由属性和方法构成的,基本格式是public class 类名{
//定义属性
private/public 数据类型 属性名;
//定义方法
publ
- android activity与viewpager+fragment的生命周期问题
肆无忌惮_
viewpager
有一个Activity里面是ViewPager,ViewPager里面放了两个Fragment。
第一次进入这个Activity。开启了服务,并在onResume方法中绑定服务后,对Service进行了一定的初始化,其中调用了Fragment中的一个属性。
super.onResume();
bindService(intent, conn, BIND_AUTO_CREATE);
- base64Encode对图片进行编码
843977358
base64图片encoder
/**
* 对图片进行base64encoder编码
*
* @author mrZhang
* @param path
* @return
*/
public static String encodeImage(String path) {
BASE64Encoder encoder = null;
byte[] b = null;
I
- Request Header简介
aigo
servlet
当一个客户端(通常是浏览器)向Web服务器发送一个请求是,它要发送一个请求的命令行,一般是GET或POST命令,当发送POST命令时,它还必须向服务器发送一个叫“Content-Length”的请求头(Request Header) 用以指明请求数据的长度,除了Content-Length之外,它还可以向服务器发送其它一些Headers,如:
- HttpClient4.3 创建SSL协议的HttpClient对象
alleni123
httpclient爬虫ssl
public class HttpClientUtils
{
public static CloseableHttpClient createSSLClientDefault(CookieStore cookies){
SSLContext sslContext=null;
try
{
sslContext=new SSLContextBuilder().l
- java取反 -右移-左移-无符号右移的探讨
百合不是茶
位运算符 位移
取反:
在二进制中第一位,1表示符数,0表示正数
byte a = -1;
原码:10000001
反码:11111110
补码:11111111
//异或: 00000000
byte b = -2;
原码:10000010
反码:11111101
补码:11111110
//异或: 00000001
- java多线程join的作用与用法
bijian1013
java多线程
对于JAVA的join,JDK 是这样说的:join public final void join (long millis )throws InterruptedException Waits at most millis milliseconds for this thread to die. A timeout of 0 means t
- Java发送http请求(get 与post方法请求)
bijian1013
javaspring
PostRequest.java
package com.bijian.study;
import java.io.BufferedReader;
import java.io.DataOutputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.net.HttpURL
- 【Struts2二】struts.xml中package下的action配置项默认值
bit1129
struts.xml
在第一部份,定义了struts.xml文件,如下所示:
<!DOCTYPE struts PUBLIC
"-//Apache Software Foundation//DTD Struts Configuration 2.3//EN"
"http://struts.apache.org/dtds/struts
- 【Kafka十三】Kafka Simple Consumer
bit1129
simple
代码中关于Host和Port是割裂开的,这会导致单机环境下的伪分布式Kafka集群环境下,这个例子没法运行。
实际情况是需要将host和port绑定到一起,
package kafka.examples.lowlevel;
import kafka.api.FetchRequest;
import kafka.api.FetchRequestBuilder;
impo
- nodejs学习api
ronin47
nodejs api
NodeJS基础 什么是NodeJS
JS是脚本语言,脚本语言都需要一个解析器才能运行。对于写在HTML页面里的JS,浏览器充当了解析器的角色。而对于需要独立运行的JS,NodeJS就是一个解析器。
每一种解析器都是一个运行环境,不但允许JS定义各种数据结构,进行各种计算,还允许JS使用运行环境提供的内置对象和方法做一些事情。例如运行在浏览器中的JS的用途是操作DOM,浏览器就提供了docum
- java-64.寻找第N个丑数
bylijinnan
java
public class UglyNumber {
/**
* 64.查找第N个丑数
具体思路可参考 [url] http://zhedahht.blog.163.com/blog/static/2541117420094245366965/[/url]
*
题目:我们把只包含因子
2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14
- 二维数组(矩阵)对角线输出
bylijinnan
二维数组
/**
二维数组 对角线输出 两个方向
例如对于数组:
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
slash方向输出:
1
5 2
9 6 3
13 10 7 4
14 11 8
15 12
16
backslash输出:
4
3
- [JWFD开源工作流设计]工作流跳跃模式开发关键点(今日更新)
comsci
工作流
既然是做开源软件的,我们的宗旨就是给大家分享设计和代码,那么现在我就用很简单扼要的语言来透露这个跳跃模式的设计原理
大家如果用过JWFD的ARC-自动运行控制器,或者看过代码,应该知道在ARC算法模块中有一个函数叫做SAN(),这个函数就是ARC的核心控制器,要实现跳跃模式,在SAN函数中一定要对LN链表数据结构进行操作,首先写一段代码,把
- redis常见使用
cuityang
redis常见使用
redis 通常被认为是一个数据结构服务器,主要是因为其有着丰富的数据结构 strings、map、 list、sets、 sorted sets
引入jar包 jedis-2.1.0.jar (本文下方提供下载)
package redistest;
import redis.clients.jedis.Jedis;
public class Listtest
- 配置多个redis
dalan_123
redis
配置多个redis客户端
<?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi=&quo
- attrib命令
dcj3sjt126com
attr
attrib指令用于修改文件的属性.文件的常见属性有:只读.存档.隐藏和系统.
只读属性是指文件只可以做读的操作.不能对文件进行写的操作.就是文件的写保护.
存档属性是用来标记文件改动的.即在上一次备份后文件有所改动.一些备份软件在备份的时候会只去备份带有存档属性的文件.
- Yii使用公共函数
dcj3sjt126com
yii
在网站项目中,没必要把公用的函数写成一个工具类,有时候面向过程其实更方便。 在入口文件index.php里添加 require_once('protected/function.php'); 即可对其引用,成为公用的函数集合。 function.php如下:
<?php /** * This is the shortcut to D
- linux 系统资源的查看(free、uname、uptime、netstat)
eksliang
netstatlinux unamelinux uptimelinux free
linux 系统资源的查看
转载请出自出处:http://eksliang.iteye.com/blog/2167081
http://eksliang.iteye.com 一、free查看内存的使用情况
语法如下:
free [-b][-k][-m][-g] [-t]
参数含义
-b:直接输入free时,显示的单位是kb我们可以使用b(bytes),m
- JAVA的位操作符
greemranqq
位运算JAVA位移<<>>>
最近几种进制,加上各种位操作符,发现都比较模糊,不能完全掌握,这里就再熟悉熟悉。
1.按位操作符 :
按位操作符是用来操作基本数据类型中的单个bit,即二进制位,会对两个参数执行布尔代数运算,获得结果。
与(&)运算:
1&1 = 1, 1&0 = 0, 0&0 &
- Web前段学习网站
ihuning
Web
Web前段学习网站
菜鸟学习:http://www.w3cschool.cc/
JQuery中文网:http://www.jquerycn.cn/
内存溢出:http://outofmemory.cn/#csdn.blog
http://www.icoolxue.com/
http://www.jikexue
- 强强联合:FluxBB 作者加盟 Flarum
justjavac
r
原文:FluxBB Joins Forces With Flarum作者:Toby Zerner译文:强强联合:FluxBB 作者加盟 Flarum译者:justjavac
FluxBB 是一个快速、轻量级论坛软件,它的开发者是一名德国的 PHP 天才 Franz Liedke。FluxBB 的下一个版本(2.0)将被完全重写,并已经开发了一段时间。FluxBB 看起来非常有前途的,
- java统计在线人数(session存储信息的)
macroli
javaWeb
这篇日志是我写的第三次了 前两次都发布失败!郁闷极了!
由于在web开发中常常用到这一部分所以在此记录一下,呵呵,就到备忘录了!
我对于登录信息时使用session存储的,所以我这里是通过实现HttpSessionAttributeListener这个接口完成的。
1、实现接口类,在web.xml文件中配置监听类,从而可以使该类完成其工作。
public class Ses
- bootstrp carousel初体验 快速构建图片播放
qiaolevip
每天进步一点点学习永无止境bootstrap纵观千象
img{
border: 1px solid white;
box-shadow: 2px 2px 12px #333;
_width: expression(this.width > 600 ? "600px" : this.width + "px");
_height: expression(this.width &
- SparkSQL读取HBase数据,通过自定义外部数据源
superlxw1234
sparksparksqlsparksql读取hbasesparksql外部数据源
关键字:SparkSQL读取HBase、SparkSQL自定义外部数据源
前面文章介绍了SparSQL通过Hive操作HBase表。
SparkSQL从1.2开始支持自定义外部数据源(External DataSource),这样就可以通过API接口来实现自己的外部数据源。这里基于Spark1.4.0,简单介绍SparkSQL自定义外部数据源,访
- Spring Boot 1.3.0.M1发布
wiselyman
spring boot
Spring Boot 1.3.0.M1于6.12日发布,现在可以从Spring milestone repository下载。这个版本是基于Spring Framework 4.2.0.RC1,并在Spring Boot 1.2之上提供了大量的新特性improvements and new features。主要包含以下:
1.提供一个新的sprin