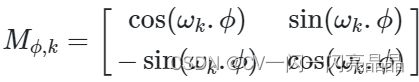transformer位置编码最详细的解析
位置编码positional encoding
-
- 1. 位置编码是什么，为什么需要它？
- 2. transformer提出的位置编码方法
- 3. 直觉
- 4. 其他细节
- 5. 相对位置
- 6. 常见问题解答
1. 位置编码是什么，为什么需要它？
位置和词语的顺序是任何语言的重要组成部分。它们定义了语法，从而决定了句子的实际语义。循环神经网络（RNN）本质上考虑了词语的顺序；它们按照顺序逐个解析句子中的词语。这样可以将词语的顺序整合到RNN的主干中。
但是Transformer架构放弃了循环机制，转而采用多头自注意机制，避免了RNN的循环方法，大大加快训练时间。从理论上讲，它可以捕捉到句子中更长的依赖关系。
由于句子中的每个词语同时通过Transformer的编码器/解码器堆栈，模型本身对于每个词语的位置/顺序没有任何概念。因此，我们需要一种方法将词语的顺序融入到我们的模型中。
为了使模型具有一定的顺序感，一种可能的解决方案是为每个词语添加关于其在句子中位置的信息。我们称这个“信息片段”为位置编码。
一个方法是为每个时间步分配一个在[0, 1]范围内的数字，其中0表示第一个词，1表示最后一个时间步。它引入的一个问题是无法确定在特定范围内有多少个词。换句话说，时间步的差值在不同句子中没有一致的含义。
另一个方法是线性地为每个时间步分配一个数字。也就是说，第一个词被赋予“1”，第二个词被赋予“2”，依此类推。这种方法的问题是，不仅值可能变得非常大，而且我们的模型可能面临比训练中的句子更长的句子。此外，我们的模型可能不会看到具有特定长度的任何样本，这会影响我们模型的泛化能力。
理想情况下，应满足以下几个条件：
它应为每个时间步（词语在句子中的位置）输出一个唯一的编码。
不同长度的句子之间的任意两个时间步之间的距离应保持一致。
我们的模型应能适应更长的句子而不需要额外的努力。其值应该受到限制。
它必须是确定性的。
2. transformer提出的位置编码方法
作者提出的编码方法是一种简单而巧妙的技术，满足上述所有标准。首先，它不是一个单独的数字，而是一个包含有关句子中特定位置信息的d维向量。其次，这种编码并没有集成到模型本身中。相反，这个向量用于为每个单词提供关于其在句子中位置的信息。换句话说，我们增强了模型的输入，注入了单词的顺序。
假设t是输入句子中的目标位置，
是其对应的编码，d是编码的维度（其中 d≡2 0）。那么
将是产生输出向量
的函数，定义如下：
其中
从函数定义中可以得出，频率沿着向量维度递减。因此，它形成了从2
π到的10000⋅2π几何级数。
您还可以将位置嵌入
想象为一个包含每个频率的正弦和余弦对的向量（注意d可被2整除）：
3. 直觉
这些正弦和余弦的组合如何表示位置/顺序？实际上非常简单，假设想以二进制格式表示一个数字，那么会是什么样子？
观察不同位之间的变化率。最低有效位（LSB）在每个数字上交替变化，次低位在每两个数字上旋转，依此类推。
但在浮点数世界中使用二进制值会浪费空间。因此，我们可以使用它们的浮点连续对应物——正弦函数。事实上，它们等同于交替位。而且，通过降低它们的频率，我们可以从红色位过渡到橙色位。
4. 其他细节
之前提过，位置编码用于为输入的单词提供位置信息。但是它是如何实现的呢？事实上，原始论文在实际嵌入之上添加了位置编码。对于句子[w1,…wn]中的每个单词wt，计算对应的嵌入并馈送给模型的过程如下：
为了使这个求和过程成立，我们保持位置编码的维度与单词嵌入的维度相等，即dword embedding=dpostional embedding
5. 相对位置
正弦余弦位置编码的另一个特点是它能够轻松地关注相对位置。以下是原始论文中的一句引用：
我们选择这个函数是因为我们假设它能够使模型轻松地学习通过相对位置进行关注，因为对于任何固定的偏移量k，PEpos+k可以表示为PEpos的线性函数。
为什么呢？因为对于每个对应于频率的正弦余弦对，存在一个线性变换
（与t无关）满足以下等式：
证明：
设M为 2×2的矩阵，我们想要找到u1,v1,u2和v2使得：
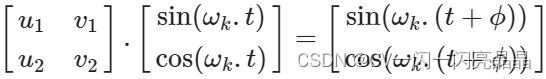
通过应用加法定理，我们可以将右边展开如下：
从而得到以下两个方程：
通过解上述方程，我们得到：
因此，最终的变换矩阵M为：
可以看到，最终的变换不依赖于t。可以找到与旋转矩阵非常相似的矩阵M。
类似地，我们可以找到其他正弦余弦对的M，最终允许我们表示为
对于任何固定偏移量ϕ的线性函数
。这个特性使得模型能够轻松地学习通过相对位置进行关注。
正弦余弦位置编码的另一个特性是相邻时间步之间的距离是对称的，并且随时间衰减得很好。
6. 常见问题解答
1. 为什么位置编码与词嵌入相加而不是连接起来？
我没有找到这个问题的理论原因。由于相加（与连接相比）可以节省模型的参数，所以将初始问题改为“将位置编码添加到单词中是否有任何缺点？”是合理的。我会说，不一定！
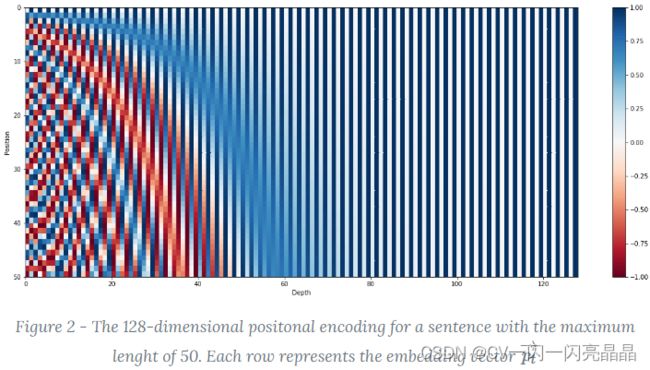
图2 会发现只有整个嵌入的前几个维度用于存储位置信息（嵌入维度为512，示例很小）。由于Transformer中的嵌入是从头开始训练的，参数可能设置为词的语义不会存储在前几个维度中，以避免干扰位置编码。
出于同样的原因，我认为最终的Transformer可以将词的语义与其位置信息分开。此外，没有理由将可分离性视为优势。也许相加为模型提供了一个良好的特征来源。
2. 位置信息在到达上层后不会消失吗？
Transformer架构配备了残差连接。因此，来自模型输入（包含位置编码）的信息可以有效地传播到处理更复杂交互的更深层。
3. 为什么同时使用正弦和余弦？
就个人而言，我认为只有同时使用正弦和余弦，我们才能将sin(x+k)和cos(x+k)表达为sin(x)和cos(x)的线性变换。似乎无法通过单一的正弦或余弦做到同样的事情。
参考文档：positional_encoding