基于四阶累积量的MUSIC算法与MUSIC-like算法(DOA估计)
DOA估计是阵列信号处理中的一个重要分支,Music(Multiple signal classification,多重信号分类)算法是相对比较经典的算法。在这里简单介绍下Music算法以及基于四阶累积量的Music的算法。
一、信号模型介绍
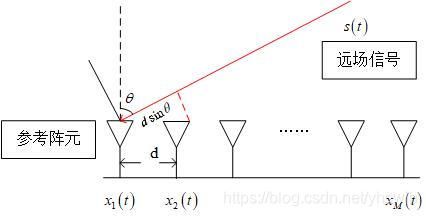
如图1所示, M M M个全向阵元组成的均匀线阵,阵元间距为 d d d,其中左侧第一个阵元为参考阵元,则参考点接收的入射信号为
x 1 ( t ) = s ( t ) e j ω t x_{1}(t)=s(t) e^{j \omega t} x1(t)=s(t)ejωt
其中, s ( t ) s(t) s(t)为信号的复振幅, ω \omega ω为信号的角频率。
阵元 m m m接收的信号为
x m ( t ) = s [ t − τ m ( θ ) ] e j ω [ t − τ m ( θ ) ] x_{m}(t)=s\left[t-\tau_{m}(\theta)\right] e^{j \omega\left[t-\tau_{m}(\theta)\right]} xm(t)=s[t−τm(θ)]ejω[t−τm(θ)]
其中, τ m ( θ ) \tau_{m}(\theta) τm(θ)为阵元 m m m接收到的入射波相对于参考点入射波的延时, θ \theta θ为入射角,也称为波达方向。对于窄带信号而言,相对于 τ m ( θ ) \tau_{m}(\theta) τm(θ)时间延迟的信号复包络变化可以忽略,则可以得到
s [ t − τ m ( θ ) ] ≈ s ( t ) s\left[t-\tau_{m}(\theta)\right]\approx s(t) s[t−τm(θ)]≈s(t)
因此可以得到
x m ( t ) = s ( t ) e j ω t e − j ω τ m = x 1 ( t ) e − j ω τ m x_{m}(t)=s(t) e^{j \omega t} e^{-j \omega \tau_{m}}=x_{1}(t) e^{-j \omega \tau_{m}} xm(t)=s(t)ejωte−jωτm=x1(t)e−jωτm
假设有 K ( K > M ) K(K>M) K(K>M)个远场窄带信号源入射该阵列上,则第 m m m个阵元接收到的信号可以表示为:
x m ( t ) = ∑ k = 1 K s k ( t ) e − j ( m − 1 ) τ k + n m ( t ) = ∑ k = 1 K s k ( t ) a m ( θ k ) + n m ( t ) m = 1 , 2 , ⋯ , M \begin{aligned} x_{m}(t) &=\sum_{k=1}^{K} s_{k}(t) e^{-j(m-1) \tau_{k}}+n_{m}(t) \\ &=\sum_{k=1}^{K} s_{k}(t) a_{m}\left(\theta_{k}\right)+n_{m}(t) \quad m=1,2, \cdots, M \end{aligned} xm(t)=k=1∑Ksk(t)e−j(m−1)τk+nm(t)=k=1∑Ksk(t)am(θk)+nm(t)m=1,2,⋯,M
其中 , τ k = 2 π d sin θ k / λ \tau_{k}=2\pi d\sin\theta_{k}/\lambda τk=2πdsinθk/λ, a ( θ k ) = [ 1 , e − j 2 π d sin θ k / λ , ⋯ , e − j 2 π ( M − 1 ) d sin θ k / λ ] a\left(\theta_{k}\right)=\left[1, e^{-j 2 \pi d \sin \theta_{k} / \lambda}, \cdots, e^{-j 2 \pi(M-1) d \sin \theta_{k} / \lambda}\right] a(θk)=[1,e−j2πdsinθk/λ,⋯,e−j2π(M−1)dsinθk/λ]表示对于入射角 θ k \theta_{k} θk 对应的导向矢量, θ k \theta_{k} θk表示第 k k k个信号源的入射方向。
为了方便描述,阵列接收的信号写成矩阵形式可以表述为
X = A S + N \mathbf{X}=\mathbf{A} \mathbf{S}+\mathbf{N} X=AS+N
其中 X = [ x 1 ( t ) , x 2 ( t ) , ⋯ , x M ( t ) ] T \mathbf{X}=\left[x_{1}(t), x_{2}(t), \cdots, x_{M}(t)\right]^{T} X=[x1(t),x2(t),⋯,xM(t)]T表示接收信号, A = [ a ( θ 1 ) , a ( θ 2 ) , ⋯ , a ( θ K ) ] T \mathbf{A}=\left[a(\theta_{1}), a(\theta_{2}), \cdots, a(\theta_{K})\right]^{T} A=[a(θ1),a(θ2),⋯,a(θK)]T阵列导向矢量矩阵, S = [ s 1 ( t ) , s 2 ( t ) , ⋯ , x K ( t ) ] T \mathbf{S}=\left[s_{1}(t), s_{2}(t), \cdots, x_{K}(t)\right]^{T} S=[s1(t),s2(t),⋯,xK(t)]T 表示信号, N = [ n 1 ( t ) , n 2 ( t ) , ⋯ , n M ( t ) ] T \mathbf{N}=\left[n_{1}(t), n_{2}(t), \cdots, n_{M}(t)\right]^{T} N=[n1(t),n2(t),⋯,nM(t)]T 表示阵列接收的噪声矢量,而且 n i ( t ) n_i(t) ni(t)为零均值,方差为 σ 2 \sigma^2 σ2 的相互独立的白噪声,也就是说
E [ n i ( t ) n j ∗ ( t ) ] = { σ 2 i = j 0 i ≠ j E\left[n_{i}(t) n_{j}^{*}(t)\right]=\left\{\begin{array}{ll} \sigma^{2} & i=j \\ 0 & i \neq j \end{array}\right. E[ni(t)nj∗(t)]={σ20i=ji=j
二、高阶统计量介绍
高阶统计量指高于二阶的统计量。高阶矩、高阶矩谱、高阶累积量以及高阶累积量谱都属于高阶统计量,下面对其概念和性质进行简单的介绍。
对于概率密度为 f ( x ) f\left( x \right) f(x)的随机变量 x x x,其第一特征函数为:
φ ( ω ) = E ( e j ω x ) = ∫ − ∞ + ∞ f ( x ) e j ω x d x \varphi \left( \omega \right)=E\left( {{e}^{j\omega x}} \right)=\int_{-\infty }^{+\infty }{f\left( x \right){{e}^{j\omega x}}dx} φ(ω)=E(ejωx)=∫−∞+∞f(x)ejωxdx
其第二类特征函数为:
ψ ( ω ) = ln φ ( ω ) \psi \left( \omega \right)=\ln \varphi \left( \omega \right) ψ(ω)=lnφ(ω)
对于随机变量 x x x的 k k k阶矩可以表示为:
m k = E [ x k ] = ∫ − ∞ + ∞ x k f ( x ) d x {{m}_{k}}=E\left[ {{x}^{k}} \right]=\int_{-\infty }^{+\infty }{{{x}^{k}}f\left( x \right)dx} mk=E[xk]=∫−∞+∞xkf(x)dx
其 k k k阶累积量可以表示为:
c k = ( − j ) k d k ψ ( ω ) d ω k ∣ ω = 0 {{c}_{k}}={{\left( -j \right)}^{k}}\frac{{{d}^{k}}\psi \left( \omega \right)}{d{{\omega }^{k}}}{{|}_{\omega =0}} ck=(−j)kdωkdkψ(ω)∣ω=0
对于一组随机变量 { x 1 , x 2 , ⋯ , x n } \left\{ {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right\} {x1,x2,⋯,xn} 可以得到其多维第一类特征函数 φ ( ω 1 , ω 2 , ⋯ , ω n ) = 1 + ∑ 1 ≤ r ≤ N j r k 1 ! k 2 ! ⋯ k n ! m k 1 k 2 − k n ω 1 k 1 ω 2 k 2 ⋯ ω n k n + o ( ∣ ω ∣ N ) \varphi \left( {{\omega }_{1}},{{\omega }_{2}},\cdots ,{{\omega }_{n}} \right)=1+\sum\limits_{1\le r\le N}{\frac{{{j}^{r}}}{{{k}_{1}}!{{k}_{2}}!\cdots {{k}_{n}}!}}{{m}_{{{k}_{1}}{{k}_{2}}-{{k}_{n}}}}\omega _{1}^{{{k}_{1}}}\omega _{2}^{{{k}_{2}}}\cdots \omega _{n}^{{{k}_{n}}}+o\left( |\mathbf{\omega }{{|}^{N}} \right) φ(ω1,ω2,⋯,ωn)=1+1≤r≤N∑k1!k2!⋯kn!jrmk1k2−knω1k1ω2k2⋯ωnkn+o(∣ω∣N)
其中 r = k 1 + k 2 + ⋯ k n , ω = ω 1 , ω 2 , ⋯ , ω n r={{k}_{1}}+{{k}_{2}}+\cdots {{k}_{n}},\mathbf{\omega }={{\omega }_{1}},{{\omega }_{2}},\cdots ,{{\omega }_{n}} r=k1+k2+⋯kn,ω=ω1,ω2,⋯,ωn
其 r r r阶矩可以表示为:
m x 1 k 1 , x 2 k 2 , ⋯ , x n k n = Δ E [ x 1 k 1 , x 2 k 2 , ⋯ , x n k n ] = ( − j ) r [ ∂ r φ ( ω 1 , ω 2 , ⋯ , ω n ) ∂ ω 1 k 1 ∂ ω 2 k 2 ⋯ ∂ ω n k n ] ∣ ω 1 = ω 2 = ⋯ ω n = 0 {{m}_{x_{1}^{{{k}_{1}}},x_{2}^{{{k}_{2}}},\cdots ,x_{n}^{{{k}_{n}}}}}\overset{\Delta }{\mathop{=}}\,E\left[ x_{1}^{{{k}_{1}}},x_{2}^{{{k}_{2}}},\cdots ,x_{n}^{{{k}_{n}}} \right]={{\left( -j \right)}^{r}}\left[ \frac{{{\partial }^{r}}\varphi \left( {{\omega }_{1}},{{\omega }_{2}},\cdots ,{{\omega }_{n}} \right)}{\partial \omega _{1}^{{{k}_{1}}}\partial \omega _{2}^{{{k}_{2}}}\cdots \partial \omega _{n}^{{{k}_{n}}}} \right]{{|}_{{{\omega }_{1}}={{\omega }_{2}}=\cdots {{\omega }_{n}}=0}} mx1k1,x2k2,⋯,xnkn=ΔE[x1k1,x2k2,⋯,xnkn]=(−j)r[∂ω1k1∂ω2k2⋯∂ωnkn∂rφ(ω1,ω2,⋯,ωn)]∣ω1=ω2=⋯ωn=0
对于一组随机变量 { x 1 , x 2 , ⋯ , x n } \left\{ {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right\} {x1,x2,⋯,xn}可以得到其多维第二类特征函数 ψ ( ω 1 , ω 2 , ⋯ , ω n ) = ∑ 1 ≤ r ≤ N j r k 1 ! k 2 ! ⋯ k n ! c k k k 2 − k n ω 1 k 1 ω 1 k 2 ⋯ ω n k n + o ( ω ∣ N ) \psi \left( {{\omega }_{1}},{{\omega }_{2}},\cdots ,{{\omega }_{n}} \right)=\sum\limits_{1\le r\le N}{\frac{{{j}^{r}}}{{{k}_{1}}!{{k}_{2}}!\cdots {{k}_{n}}!}}{{c}_{{{k}_{k}}{{k}_{2}}-{{k}_{n}}}}\omega _{1}^{{{k}_{1}}}\omega _{1}^{{{k}_{2}}}\cdots \omega _{n}^{{{k}_{n}}}+o\left( {{\left. \mathbf{\omega } \right|}^{N}} \right) ψ(ω1,ω2,⋯,ωn)=1≤r≤N∑k1!k2!⋯kn!jrckkk2−knω1k1ω1k2⋯ωnkn+o(ω∣N)
其 r r r阶累积量可以表示为:
c u m ( x 1 k 1 , x 2 k 2 , ⋯ , x n k n ) = ( − j ) r [ ∂ r ψ ( ω 1 , ω 2 , ⋯ , ω n ) ∂ ω 1 k 1 ∂ ω 2 k 2 ⋯ ∂ ω n k n ] ∣ ω 1 = ω 2 = ⋯ ω n = 0 cum\left( x_{1}^{{{k}_{1}}},x_{2}^{{{k}_{2}}},\cdots ,x_{n}^{{{k}_{n}}} \right)={{\left( -j \right)}^{r}}\left[ \frac{{{\partial }^{r}}\psi \left( {{\omega }_{1}},{{\omega }_{2}},\cdots ,{{\omega }_{n}} \right)}{\partial \omega _{1}^{{{k}_{1}}}\partial \omega _{2}^{{{k}_{2}}}\cdots \partial \omega _{n}^{{{k}_{n}}}} \right]{{|}_{{{\omega }_{1}}={{\omega }_{2}}=\cdots {{\omega }_{n}}=0}} cum(x1k1,x2k2,⋯,xnkn)=(−j)r[∂ω1k1∂ω2k2⋯∂ωnkn∂rψ(ω1,ω2,⋯,ωn)]∣ω1=ω2=⋯ωn=0
由于高阶累积量的复杂性以及计算量大等因素的影响,一般在实际应用中常常采用四阶或四阶以下的累积量。
零均值复平稳随机序列的四阶累积量定义为
C 4 , x ( k 1 , k 2 , k 3 ) = E { x ( n ) x ∗ ( n + k 1 ) x ( n + k 2 ) x ∗ ( n + k 3 ) } − E { x ( n ) x ∗ ( n + k 1 ) } E { x ( n + k 2 ) x ∗ ( n + k 3 ) } − E { x ( n ) x ( n + k 2 ) } E { x ∗ ( n + k 1 ) x ∗ ( n + k 3 ) } − E { x ( n ) x ∗ ( n + k 3 ) } E { x ∗ ( n + k 1 ) x ( n + k 2 ) } \begin{aligned} C_{4, x}\left(k_{1}, k_{2}, k_{3}\right)=& E\left\{x(n) x^{*}\left(n+k_{1}\right) x\left(n+k_{2}\right) x^{*}\left(n+k_{3}\right)\right\} \\ &-E\left\{x(n) x^{*}\left(n+k_{1}\right)\right\} E\left\{x\left(n+k_{2}\right) x^{*}\left(n+k_{3}\right)\right\} \\ &-E\left\{x(n) x\left(n+k_{2}\right)\right\} E\left\{x^{*}\left(n+k_{1}\right) x^{*}\left(n+k_{3}\right)\right\} \\ &-E\left\{x(n) x^{*}\left(n+k_{3}\right)\right\} E\left\{x^{*}\left(n+k_{1}\right) x\left(n+k_{2}\right)\right\} \end{aligned} C4,x(k1,k2,k3)=E{x(n)x∗(n+k1)x(n+k2)x∗(n+k3)}−E{x(n)x∗(n+k1)}E{x(n+k2)x∗(n+k3)}−E{x(n)x(n+k2)}E{x∗(n+k1)x∗(n+k3)}−E{x(n)x∗(n+k3)}E{x∗(n+k1)x(n+k2)}
由于复信号的对称性,上式中右边第三项为零,这样四阶累积量可以简化为
C 4 , x ( k 1 , k 2 , k 3 ) = E { x ( n ) x ∗ ( n + k 1 ) x ( n + k 2 ) x ∗ ( n + k 3 ) } − E { x ( n ) x ∗ ( n + k 1 ) } E { x ( n + k 2 ) x ∗ ( n + k 3 ) } − E { x ( n ) x ∗ ( n + k 3 ) } E { x ∗ ( n + k 1 ) x ( n + k 2 ) } \begin{aligned} C_{4, x}\left(k_{1}, k_{2}, k_{3}\right) &=E\left\{x(n) x^{*}\left(n+k_{1}\right) x\left(n+k_{2}\right) x^{*}\left(n+k_{3}\right)\right\} \\ &-E\left\{x(n) x^{*}\left(n+k_{1}\right)\right\} E\left\{x\left(n+k_{2}\right) x^{*}\left(n+k_{3}\right)\right\} \\ &-E\left\{x(n) x^{*}\left(n+k_{3}\right)\right\} E\left\{x^{*}\left(n+k_{1}\right) x\left(n+k_{2}\right)\right\} \end{aligned} C4,x(k1,k2,k3)=E{x(n)x∗(n+k1)x(n+k2)x∗(n+k3)}−E{x(n)x∗(n+k1)}E{x(n+k2)x∗(n+k3)}−E{x(n)x∗(n+k3)}E{x∗(n+k1)x(n+k2)}
在实际的应用中,通常取 k 1 = k 2 = k 3 = 0 {{k}_{1}}={{k}_{2}}={{k}_{3}}=0 k1=k2=k3=0,因此对于复信号的四阶累积量可以表示为
C 4 , x = E { x ( n ) x ∗ ( n ) x ( n ) x ∗ ( n ) } − E { x ( n ) x ∗ ( n ) } E { x ( n ) x ∗ ( n ) } − E { x ( n ) x ∗ ( n ) } E { x ∗ ( n ) x ( n ) } \begin{aligned} & {{C}_{4,x}}=E\left\{ x(n){{x}^{*}}\left( n \right)x\left( n \right){{x}^{*}}\left( n \right) \right\} \\ & \ \ \ \ \ \ -E\left\{ x(n){{x}^{*}}\left( n \right) \right\}E\left\{ x\left( n \right){{x}^{*}}\left( n \right) \right\} \\ & \ \ \ \ \ \ -E\left\{ x(n){{x}^{*}}\left( n \right) \right\}E\left\{ {{x}^{*}}\left( n \right)x\left( n \right) \right\} \\ \end{aligned} C4,x=E{x(n)x∗(n)x(n)x∗(n)} −E{x(n)x∗(n)}E{x(n)x∗(n)} −E{x(n)x∗(n)}E{x∗(n)x(n)}
高阶累积量还有以下性质:
若 { α i } i = 1 n \left\{ {{\alpha }_{i}} \right\}_{i=1}^{n} {αi}i=1n 为常数数列, { x i } i = 1 n \left\{ {{x}_{i}} \right\}_{i=1}^{n} {xi}i=1n为随机变量,则
c u m ( α 1 x 1 , α 2 x 2 , ⋯ , α n x n ) = ( ∏ i = 1 n α i ) c u m ( x 1 , x 2 , ⋯ , x n ) cum\left( {{\alpha }_{1}}{{x}_{1}},{{\alpha }_{2}}{{x}_{2}},\cdots ,{{\alpha }_{n}}{{x}_{n}} \right)=\left( \prod\limits_{i=1}^{n}{{{\alpha }_{i}}} \right)cum\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right) cum(α1x1,α2x2,⋯,αnxn)=(i=1∏nαi)cum(x1,x2,⋯,xn)
高阶累积量对其变量具有可加性
c u m ( x 1 + y 1 , x 2 , ⋯ , x n ) = c u m ( x 1 , x 2 , ⋯ , x n ) + c u m ( y 1 , x 2 , ⋯ , x n ) cum\left( {{x}_{1}}+{{y}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right)=cum\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right)+cum\left( {{y}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right) cum(x1+y1,x2,⋯,xn)=cum(x1,x2,⋯,xn)+cum(y1,x2,⋯,xn)
若随机变量 { x i } i = 1 n \left\{ {{x}_{i}} \right\}_{i=1}^{n} {xi}i=1n与随机变量 { y i } i = 1 n \left\{ {{y}_{i}} \right\}_{i=1}^{n} {yi}i=1n统计独立,则
c u m ( x 1 + y 1 , x 2 + y 2 , ⋯ , x n + y n ) = c u m ( x 1 , x 2 , ⋯ , x n ) + c u m ( y 1 , y 2 , ⋯ , y n ) cum\left( {{x}_{1}}+{{y}_{1}},{{x}_{2}}+{{y}_{2}},\cdots ,{{x}_{n}}+{{y}_{n}} \right)=cum\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right)+cum\left( {{y}_{1}},{{y}_{2}},\cdots ,{{y}_{n}} \right) cum(x1+y1,x2+y2,⋯,xn+yn)=cum(x1,x2,⋯,xn)+cum(y1,y2,⋯,yn)
若 { x i } i = 1 n \left\{ {{x}_{i}} \right\}_{i=1}^{n} {xi}i=1n为零均值的高斯随机变量,则其四阶累积量为零,也就是
c u m ( x 1 , x 2 , ⋯ , x n ) = 0 cum\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right)=0 cum(x1,x2,⋯,xn)=0
若 { x i } i = 1 n \left\{ {{x}_{i}} \right\}_{i=1}^{n} {xi}i=1n中有任意一个非空子集独立于该子集的余集,则
c u m ( x 1 , x 2 , ⋯ , x n ) = 0 cum\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}} \right)=0 cum(x1,x2,⋯,xn)=0
由于高阶累积量具有这些优良的性质,使得高阶累积量在阵列信号处理中的应用很广泛,也具有低阶累积量不具有的性质:
抑制高斯色噪声的影响(高斯噪声的二阶以上累积量恒为零);
辨识非因果、非最小相位系统或重构非最小相位信号;
提取由于高斯性偏离引起的各种信息;
检验和表征信号中的非线性以及辨识非线性系统;
检验和表征信号中的循环平稳性以及分析和处理循环平稳信号;
高阶累积量不仅可以自动抑制高斯噪声的影响,而且也能抑制对称分布噪声的影响;高阶循环统计量则能自动抑制任何平稳(高斯与非高斯)噪声的影响。
同时,采用高阶累积量应用到波达方向估计算法而不用高阶矩来进行分析主要是基于以下的原因:
高阶累积量的使用可以避免高斯有色噪声的影响,而高阶矩却不能;
两个统计独立的随机过程之和的高阶累积量等于各个随机过程的高阶累积量之和,这样在实际处理加性信号时将带来运算上的方便,而高阶矩却不满足此性质;
独立同分布过程的高阶累量为 δ \delta δ函数,因而其傅里叶变换是多维平坦的。
三、算法原理
3.1 传统Music算法
由接收信号的模型可以看出,对 x m ( t ) x_m(t) xm(t)进行 L L L点采样,要处理的问题就变成通过输出信号 { x m ( i ) ∣ i = 1 , 2 , ⋯ , L } \left\{x_{m}(i) \mid i=1,2, \cdots, L\right\} {xm(i)∣i=1,2,⋯,L}来估计信号源的波达方向角 θ 1 , θ 2 , ⋯ θ K \theta_1,\theta_2,\cdots\theta_K θ1,θ2,⋯θK,假设噪声为零均值的高斯白噪声,已知信号和噪声互不相关,对阵列的输出 X \mathbf{X} X进行相关运算可以得到其协方差矩阵
R x = E [ X X H ] = E [ ( A S + N ) ( A S + N ) H ] = A E [ S S H ] A H + E [ N N H ] = A R s A H + R N \begin{aligned} R_{x} &=E\left[\mathbf{X X}^{H}\right]=E\left[(\mathbf{A} \mathbf{S}+\mathbf{N})(\mathbf{A} \mathbf{S}+\mathbf{N})^{H}\right] \\ &=\mathbf{A} E\left[\mathbf{S} \mathbf{S}^{H}\right] \mathbf{A}^{H}+E\left[\mathbf{N} \mathbf{N}^{H}\right]=\mathbf{A} R_{s} \mathbf{A}^{H}+R_{N} \end{aligned} Rx=E[XXH]=E[(AS+N)(AS+N)H]=AE[SSH]AH+E[NNH]=ARsAH+RN
其中 R s = E [ S S H ] R_{s}=E[\mathbf{S} \mathbf{S}^{H}] Rs=E[SSH] 表示信号的相关矩阵, R N = E [ N N H ] = σ 2 I R_{N}=E[\mathbf{N} \mathbf{N}^{H}]=\sigma^2\mathbf{I} RN=E[NNH]=σ2I为噪声的自相关矩阵, σ 2 \sigma^2 σ2表示噪声的功率, I ∈ R M × M \mathbf{I} \in R^{M \times M} I∈RM×M 为单位阵。
在实际的应用中, R x \mathbf {R_{x}} Rx通常无法直接获得 ,所以采用样本的协方差矩阵来代替真实的协方差矩阵
R ^ x = 1 L ∑ l = 1 L X ( l ) X H ( l ) \hat{R}_{x}=\frac{1}{L} \sum_{l=1}^{L} \mathbf{X}(l) \mathbf{X}^{H}(l) R^x=L1l=1∑LX(l)XH(l)
其中 R ^ x \hat{R}_{x} R^x为 R x \mathbf {R_{x}} Rx 的最大似然估计,当 L → ∞ L\to \infty L→∞时,两者是等价的,但实际情况将由于样本数有限而造成误差。
根据矩阵特征分解的理论,可对阵列协方差矩阵进行特征分解,首先考虑理想情况,即无噪声的情况: R x = A R s A H \mathbf R_{x}=\mathbf{A} R_{s} \mathbf{A}^{H} Rx=ARsAH。若 R s R_{s} Rs为非奇异矩阵,即 r a n k ( R s ) = K rank(R_{s})=K rank(Rs)=K,各个信号源两两不相干,则 r a n k ( A R s A H ) = K rank(\mathbf{A} R_{s} \mathbf{A}^{H})=K rank(ARsAH)=K,而 R x = E [ X X H ] R_{x}=E[\mathbf{X X}^{H}] Rx=E[XXH],所以 R s H = R x {{R}_{s}}^{H}={{R}_{x}} RsH=Rx ,即 R s {{R}_{s}} Rs为Hermite矩阵,它的特征值是都是实数。同时由于 R s {{R}_{s}} Rs为正定的,所以 R x = A R s A H \mathbf R_{x}=\mathbf{A} R_{s} \mathbf{A}^{H} Rx=ARsAH是半正定的,也就是说,它有 K K K个非零特征值和 M − K M-K M−K个零特征值。
当存在噪声时 R x = A R s A H + σ 2 I \mathbf R_{x}=\mathbf{A} R_{s} \mathbf{A}^{H}+\sigma^2\mathbf{I} Rx=ARsAH+σ2I ,因为 σ 2 > 0 {{\sigma }^{2}}>0 σ2>0 ,所以 R x R_{x} Rx满秩,即 R x R_{x} Rx 有 M M M个正实特征值 λ 1 , λ 2 , ⋯ , λ M \lambda_{1}, \lambda_{2}, \cdots, \lambda_{M} λ1,λ2,⋯,λM 分别对应 M M M个特征矢量 v 1 , v 2 , ⋯ , v M {{v}_{1}},{{v}_{2}},\cdots ,{{v}_{M}} v1,v2,⋯,vM 。同时由于 R x R_{x} Rx为Hermite矩阵,所以各特征向量是正交的,即 v i H v j = 0 ∀ i ≠ j v_{i}^{H}{{v}_{j}}=0\ \ \ \ \forall \ \ i\ne j viHvj=0 ∀ i=j 。与信号有关的特征值只有 K K K个分别等于矩阵 A R s A H \mathbf{A}{{R}_{s}}{{\mathbf{A}}^{H}} ARsAH的各个特征值与 σ 2 \sigma^2 σ2之和,其余 M − K M-K M−K个特征值为 σ 2 \sigma^2 σ2,即 σ 2 \sigma^2 σ2为 R x R_{x} Rx的最小特征值,其为 M − K M-K M−K 维的,在特征向量为 v 1 , v 2 , ⋯ , v M {{v}_{1}},{{v}_{2}},\cdots ,{{v}_{M}} v1,v2,⋯,vM 中,有 K K K个是与信号有关的,另外 M − K M-K M−K 个与噪声有关,因此可以利用特征分解的性质求出信号源的波达方向 θ k \theta_{k} θk。
设 λ i {{\lambda }_{i}} λi为 R x R_{x} Rx的第 i i i个特征值, v i {{v}_{i}} vi是与 λ i {{\lambda }_{i}} λi 对应的特征向量,则可以得到 R x v i = λ i v i {{R}_{x}}{{v}_{i}}={{\lambda }_{i}}{{v}_{i}} Rxvi=λivi ,同时设 λ i = σ 2 {{\lambda }_{i}}\text{=}{{\sigma }^{2}} λi=σ2是 R x R_{x} Rx的最小特征值,可以得到
R x v i = σ 2 v i i = K + 1 , K + 2 , ⋯ , M {{R}_{x}}{{v}_{i}}={{\sigma }^{2}}{{v}_{i}}\ \ \ \ i=K+1,K+2,\cdots ,M Rxvi=σ2vi i=K+1,K+2,⋯,M
将 R x = A R s A H + σ 2 I {{R}_{x}}=\mathbf{A}{{R}_{s}}{{\mathbf{A}}^{H}}+{{\sigma }^{2}}\mathbf{I} Rx=ARsAH+σ2I代入
σ 2 v i = ( A R s A H + σ 2 I ) v i {{\sigma }^{2}}{{v}_{i}}\text{=}\left( \mathbf{A}{{R}_{s}}{{\mathbf{A}}^{H}}+{{\sigma }^{2}}\mathbf{I} \right){{v}_{i}} σ2vi=(ARsAH+σ2I)vi
因为 A H A ∈ R K × K {{\mathbf{A}}^{H}}\mathbf{A}\in {{R}^{K\times K}} AHA∈RK×K 满秩矩阵,故 ( A H A ) - 1 {{\left( {{\mathbf{A}}^{H}}\mathbf{A} \right)}^{\text{-}1}} (AHA)-1 存在,同理 R s − 1 {{R}_{s}}^{-1} Rs−1存在,将上式左右两边同时乘以 R s − 1 ( A H A ) - 1 A H R_{s}^{-1}{{\left( {{\mathbf{A}}^{H}}\mathbf{A} \right)}^{\text{-}1}}{{\mathbf{A}}^{H}} Rs−1(AHA)-1AH 有
R s − 1 ( A H A ) - 1 A H A R s A H v i = 0 R_{s}^{-1}{{\left( {{\mathbf{A}}^{H}}\mathbf{A} \right)}^{\text{-}1}}{{\mathbf{A}}^{H}}\mathbf{A}{{R}_{s}}{{\mathbf{A}}^{H}}{{v}_{i}}=0 Rs−1(AHA)-1AHARsAHvi=0即
A H v i = 0 i = K + 1 , K + 2 , ⋯ , M \mathbf{A}^{H} v_{i}=0 \quad i=K+1, K+2, \cdots, M AHvi=0i=K+1,K+2,⋯,M
通过上式可以看出,噪声特征值所对应的特征向量(称为噪声特征向量) v i {{v}_{i}} vi与矩阵 A \mathbf{A} A的列向量正交,而 A \mathbf{A} A的各列是与信号源的方向相对应的,用各噪声特征向量构造噪声矩阵 E n {{E}_{n}} En ,其中
E n = { v K + 1 , v K + 2 , ⋯ , v M } {{E}_{n}}=\left\{ {{v}_{K+1}},{{v}_{K+2}},\cdots ,{{v}_{M}} \right\} En={vK+1,vK+2,⋯,vM}
将上述过程可以总结为:通过对协方差矩阵进行特征值分解,将矩阵 R x R_{x} Rx的特征值进行从大到小排序, λ 1 ≥ λ 2 ≥ ⋯ ≥ λ M {{\lambda }_{1}}\ge {{\lambda }_{2}}\ge \cdots \ge {{\lambda }_{M}} λ1≥λ2≥⋯≥λM ,其中 K K K较大的特征值对应信号, M − K M-K M−K 较小的特征值对应噪声。将 K K K个较大特征值对应的特征向量张成的子空间称为信号子空间 Ω s {{\Omega }_{s}} Ωs, M − K M-K M−K个较小的特征值对应的特征向量张成的子空间称为噪声子空间 Ω N {{\Omega }_{N}} ΩN,即
{ Ω s = span { v 1 , v 2 , ⋯ , v K } Ω N = span { v K + 1 , v K + 2 , ⋯ , v M } \left\{\begin{array}{l} \Omega_{s}=\operatorname{span}\left\{v_{1}, v_{2}, \cdots, v_{K}\right\} \\ \Omega_{N}=\operatorname{span}\left\{v_{K+1}, v_{K+2}, \cdots, v_{M}\right\} \end{array}\right. {Ωs=span{v1,v2,⋯,vK}ΩN=span{vK+1,vK+2,⋯,vM}
因为各个特征向量相互正交,故可以得到 Ω s ⊥ Ω N {{\Omega }_{s}}\bot {{\Omega }_{N}} Ωs⊥ΩN ,而的各列是与信号源的方向相对应的,显然有 a ( θ k ) ⊥ Ω N a\left( {{\theta }_{k}} \right)\bot {{\Omega }_{N}} a(θk)⊥ΩN 。
定义空间谱
P ( θ ) = 1 a H ( θ ) E n E n H a ( θ ) = 1 ∥ E n H a ( θ ) ∥ 2 2 P\left( \theta \right)=\frac{1}{{{a}^{H}}\left( \theta \right){{E}_{n}}{{E}_{n}}^{H}a\left( \theta \right)}=\frac{1}{\left\| {{E}_{n}}^{H}a\left( \theta \right) \right\|_{2}^{2}} P(θ)=aH(θ)EnEnHa(θ)1=∥∥EnHa(θ)∥∥221
当 a ( θ ) a\left( \theta \right) a(θ)与 E n {{E}_{n}} En各列正交时,该分母为零,但由于噪声的存在,它实际上为一最小值,因此 P ( θ ) P(\theta) P(θ) 有一尖峰值,使 θ \theta θ变化,通过寻找波峰来估计波达方向。
Music算法的步骤为
1):根据 个接收信号矢量得到下面协方差矩阵的估计值 R x = 1 L ∑ l = 1 L X ( l ) X H ( l ) {{R}_{x}}=\frac{1}{L}\sum\limits_{l=1}^{L}{\mathbf{X}\left( l \right){{\mathbf{X}}^{H}}\left( l \right)} Rx=L1l=1∑LX(l)XH(l) ;
2):按特征值的大小排序将与信号个数 K K K相等的特征值和对应的特征向量看作信号部分空间,将剩下的 M − K M-K M−K个特征值和特征向量看作噪声部分空间,得到噪声矩阵 E n {{E}_{n}} En ;
3):使 θ \theta θ变化,寻找 P ( θ ) P(\theta) P(θ)的峰值,即为信源方向。
MUSIC算法的提出开创了空间谱估计算法研究的新时代,促进了特征结构类算法的兴起和发展,该算法已成为空间谱估计理论体系中的标志性算法。此算法提出之前的有关算法都是针对阵列接收数据协方差矩阵进行直接处理,而MUSIC算法的基本思想则是对任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分类相对应的信号子空间和与信号分量相正交的噪声子空间,然后利用这两个子空间的正交性构造空间谱函数,通过谱峰搜索,检测信号的DOA。
正是由于MUSIC算法在特定的条件下具有很高的分辨力、估计精度及稳定性,从而吸引了大量的学者对其进行深入的研究和分析。总的来说,它用于阵列的波达方向估计有以下一些突出的优点:
多信号同时测向能力
高精度测向
对天线波束内的信号的高分辨测向
可适用于短数据情况
采用高速处理技术后可实现实时处理
3.2基于四阶累积量的Music算法
阵列输出的信号的矩阵表达形式为
X = A S + N \mathbf{X}=\mathbf{AS+N} X=AS+N
其四阶累积量矩阵为
C x = E { ( ( A S + N ) ⊗ ( A S + N ) ∗ ) ( ( A S + N ) ⊗ X ∗ ) H } − E { ( ( A S + N ) ⊗ ( A S + N ) ∗ ) } E { ( ( A S + N ) ⊗ ( A S + N ) } } ( A S + N ) ∗ ) H } − E { ( ( A S + N ) ( A S + N ) H ) } ⊗ E { ( ( A S + N ) ( A S + N ) H ) ∗ } \begin{array}{l} C_{x}=E\left\{\left((\mathbf{A} \mathbf{S}+\mathbf{N}) \otimes(\mathbf{A} \mathbf{S}+\mathbf{N})^{*}\right)\left((\mathbf{A} \mathbf{S}+\mathbf{N}) \otimes \mathbf{X}^{*}\right)^{H}\right\} \\ -E\left\{\left((\mathbf{A} \mathbf{S}+\mathbf{N}) \otimes(\mathbf{A} \mathbf{S}+\mathbf{N})^{*}\right)\right\} E\{((\mathbf{A} \mathbf{S}+\mathbf{N}) \otimes(\mathbf{A} \mathbf{S}+\mathbf{N})\}\}(\mathbf{A} \mathbf{S}+ \\ \left.\left.\mathbf{N})^{*}\right)^{H}\right\}-E\left\{\left((\mathbf{A} \mathbf{S}+\mathbf{N})(\mathbf{A} \mathbf{S}+\mathbf{N})^{H}\right)\right\} \otimes E\left\{\left((\mathbf{A} \mathbf{S}+\mathbf{N})(\mathbf{A} \mathbf{S}+\mathbf{N})^{H}\right)^{*}\right\} \end{array} Cx=E{((AS+N)⊗(AS+N)∗)((AS+N)⊗X∗)H}−E{((AS+N)⊗(AS+N)∗)}E{((AS+N)⊗(AS+N)}}(AS+N)∗)H}−E{((AS+N)(AS+N)H)}⊗E{((AS+N)(AS+N)H)∗}
同时为了简化式上式的表述,根据Kronecker 乘积的性质可以得到
C s = E { ( S ⊗ S ∗ ) ( S ⊗ S ∗ ) H } − E { ( S ⊗ S ∗ ) } E { ( S ⊗ S ∗ ) H } − E { ( S S ∗ ) } ⊗ E { ( S S ∗ ) H } \begin{array}{c} C_{s}=E\left\{\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)^{H}\right\}-E\left\{\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)\right\} E\left\{\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)^{H}\right\} \\ -E\left\{\left(\mathbf{S S}^{*}\right)\right\} \otimes E\left\{\left(\mathbf{S S}^{*}\right)^{H}\right\}\end{array} Cs=E{(S⊗S∗)(S⊗S∗)H}−E{(S⊗S∗)}E{(S⊗S∗)H}−E{(SS∗)}⊗E{(SS∗)H}
C N = E { ( N ⊗ N ∗ ) ( N ⊗ N ∗ ) H } − E { ( N ⊗ N ∗ ) } E { ( N ⊗ N ∗ ) H } − E { ( N N ∗ ) } ⊗ E { ( N N ∗ ) H } \begin{array}{c}C_{N}=E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)^{H}\right\}-E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)\right\} E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)^{H}\right\} \\ -E\left\{\left(\mathbf{N} \mathbf{N}^{*}\right)\right\} \otimes E\left\{\left(\mathbf{N} \mathbf{N}^{*}\right)^{H}\right\} \end{array} CN=E{(N⊗N∗)(N⊗N∗)H}−E{(N⊗N∗)}E{(N⊗N∗)H}−E{(NN∗)}⊗E{(NN∗)H}
C x = ( A ⊗ A ∗ ) E { ( S ⊗ S ∗ ) ( S ⊗ S ∗ ) H } ( A ⊗ A ∗ ) H + E { ( N ⊗ N ∗ ) ( N ⊗ N ∗ ) H } − ( A ⊗ A ∗ ) E { ( S ⊗ S ∗ ) } E { S ) ⊗ S ∗ ) H } ( A ⊗ A ∗ ) H − E { ( N ⊗ N ∗ ) } E { ( N ⊗ N ∗ ) H } − ( A ⊗ A ∗ ) E { ( S S ∗ ) } ⊗ E { ( S S ∗ ) H } ( A ⊗ A ∗ ) H − E { ( N N ∗ ) } ⊗ E { ( N N ∗ ) H } \begin{array}{l} C_{x}=\left(\mathbf{A} \otimes \mathbf{A}^{*}\right) E\left\{\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)^{H}\right\}\left(\mathbf{A} \otimes \mathbf{A}^{*}\right)^{H}+ \\ E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)^{H}\right\}-\left(\mathbf{A} \otimes \mathbf{A}^{*}\right) E\left\{\left(\mathbf{S} \otimes \mathbf{S}^{*}\right)\right\} E\{\mathbf{S}) \\ \left.\left.\otimes \mathbf{S}^{*}\right)^{H}\right\}\left(\mathbf{A} \otimes \mathbf{A}^{*}\right)^{H}-E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)\right\} E\left\{\left(\mathbf{N} \otimes \mathbf{N}^{*}\right)^{H}\right\}-(\mathbf{A} \\ \left.\otimes \mathbf{A}^{*}\right) E\left\{\left(\mathbf{S S}^{*}\right)\right\} \otimes E\left\{\left(\mathbf{S S}^{*}\right)^{H}\right\}\left(\mathbf{A} \otimes \mathbf{A}^{*}\right)^{H}-E\left\{\left(\mathbf{N} \mathbf{N}^{*}\right)\right\} \\ \otimes E\left\{\left(\mathbf{N} \mathbf{N}^{*}\right)^{H}\right\} \end{array} Cx=(A⊗A∗)E{(S⊗S∗)(S⊗S∗)H}(A⊗A∗)H+E{(N⊗N∗)(N⊗N∗)H}−(A⊗A∗)E{(S⊗S∗)}E{S)⊗S∗)H}(A⊗A∗)H−E{(N⊗N∗)}E{(N⊗N∗)H}−(A⊗A∗)E{(SS∗)}⊗E{(SS∗)H}(A⊗A∗)H−E{(NN∗)}⊗E{(NN∗)H}
其中 C s {{C}_{s}} Cs和 C N {{C}_{N}} CN分别是信号源和噪声的四阶累积量矩阵。
令 R = A ⊗ A ∗ R=\mathbf{A}\otimes {{\mathbf{A}}^{*}} R=A⊗A∗ ,则接收信号的四阶累积量矩阵可以表示为
C x = R C s R H + C N {{C}_{x}}=R{{C}_{s}}{{R}^{H}}+{{C}_{N}} Cx=RCsRH+CN
对 C x {{C}_{x}} Cx进行特征值分解,并将其特征值从大到小排列为 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ M 2 {{\lambda }_{1}}\ge {{\lambda }_{2}}\ge \cdots \ge {{\lambda }_{{{M}^{2}}}} λ1≥λ2≥⋯≥λM2,对应的特征向量分别为 μ 1 , μ 2 , ⋯ , μ M 2 {{\mu }_{1}},{{\mu }_{2}},\cdots ,{{\mu }_{{{M}^{2}}}} μ1,μ2,⋯,μM2 。因为 r a n k ( R C s R H ) = K 2 rank\left( R{{C}_{s}}{{R}^{H}} \right)={{K}^{2}} rank(RCsRH)=K2 ,所以和MUSIC算法类似, C x {{C}_{x}} Cx有 K 2 {{K}^{2}} K2较大的特征值和 M 2 − K 2 {{M}^{2}}-{{K}^{2}} M2−K2 较小的特征值。同时将小特征值对于的特征向量张成的空间称为噪声子空间,即
Ω N = s p a n { μ K 2 + 1 , μ K 2 + 2 , ⋯ , μ M 2 } {{\Omega }_{N}}=span\left\{ {{\mu }_{{{K}^{2}}+1}},{{\mu }_{{{K}^{2}}+2}},\cdots ,{{\mu }_{{{M}^{2}}}} \right\} ΩN=span{μK2+1,μK2+2,⋯,μM2}
同时定义信号子空间为
Ω s = s p a n { ( a ( θ 1 ) ⊗ a ∗ ( θ 1 ) ) , ( a ( θ 2 ) ⊗ a ∗ ( θ 2 ) ) , ⋯ , ( a ( θ K ) ⊗ a ∗ ( θ K ) ) } {{\Omega }_{s}}=span\left\{ \left( a\left( {{\theta }_{1}} \right)\otimes {{a}^{*}}\left( {{\theta }_{1}} \right) \right),\left( a\left( {{\theta }_{2}} \right)\otimes {{a}^{*}}\left( {{\theta }_{2}} \right) \right),\cdots ,\left( a\left( {{\theta }_{K}} \right)\otimes {{a}^{*}}\left( {{\theta }_{K}} \right) \right) \right\} Ωs=span{(a(θ1)⊗a∗(θ1)),(a(θ2)⊗a∗(θ2)),⋯,(a(θK)⊗a∗(θK))}
由于信号子空间和噪声子空间相互正交,所以可以得到正交条件为
R H μ i = 0 i = K 2 + 1 , K 2 + 2 , ⋯ , M 2 {{R}^{H}}{{\mu }_{i}}=0\ \ \ \ \ \ i={{K}^{2}}+1,{{K}^{2}}+2,\cdots ,{{M}^{2}} RHμi=0 i=K2+1,K2+2,⋯,M2
定义噪声矩阵
E n = { μ K 2 + 1 , μ K 2 + 2 , ⋯ , μ M 2 } {{E}_{n}}=\left\{ {{\mu }_{{{K}^{2}}+1}},{{\mu }_{{{K}^{2}}+2}},\cdots ,{{\mu }_{{{M}^{2}}}} \right\} En={μK2+1,μK2+2,⋯,μM2}
则基于四阶累积量矩阵的MUSIC算法可以表示为
P ( θ ) = 1 ∥ E n H ⋅ [ a ( θ ) ⊗ a ∗ ( θ ) ] ∥ 2 2 P\left( \theta \right)=\frac{1}{\left\| E_{n}^{H}\centerdot \left[ a\left( \theta \right)\otimes {{a}^{*}}\left( \theta \right) \right] \right\|_{2}^{2}} P(θ)=∥EnH⋅[a(θ)⊗a∗(θ)]∥221
因此基于四阶累积量的Music算法的步骤可以总结如下:
1) 根据各阵元收到的信号构造复解析形式,从而得到矩阵 X \mathbf{X} X ;
2) 求矩阵 X \mathbf{X} X 的四阶累积量矩阵 C x {{C}_{x}} Cx ;
3) 对 C x {{C}_{x}} Cx进行特征分解,计算四阶累积量的空间谱;
4) 搜索谱峰就可以得到信源方向。
基于四阶累积量的MUSIC算法与MUSIC算法类似,但是不同之处在于利用四阶累积量矩阵代替原始的协方差矩阵,将原始的导向矢量换成导向矢量的Kronecker积,虽然在计算量上有所增加,但是却能对高斯噪声进行很好地抑制,达到更好的超分辨性能。
3.3基于四阶累积量的Music-like算法
由上文的叙述可以了解到,阵列的接收矢量 X \mathbf{X} X的秩与信号源个数相等,并且为 K K K,满足 K ≤ M K\le M K≤M ,因此可以得到矩阵 X ⊗ X ∗ \mathbf{X}\otimes {{\mathbf{X}}^{*}} X⊗X∗的秩满足 r a n k ( X ⊗ X ∗ ) ≤ K 2 rank\left( \mathbf{X}\otimes {{\mathbf{X}}^{*}} \right)\le {{K}^{2}} rank(X⊗X∗)≤K2 ,所以可以估计的信源数目至少为 M 2 − K 2 {{M}^{2}}-{{K}^{2}} M2−K2 ,通过对 C x {{C}_{x}} Cx进行特征分解,并将特征值按从小到大进行排序为 λ 1 , λ 2 , ⋯ , λ M 2 {{\lambda }_{1}},{{\lambda }_{2}},\cdots ,{{\lambda }_{{{M}^{2}}}} λ1,λ2,⋯,λM2,对应特征向量为 e 1 , e 2 , ⋯ , e M 2 {{\mathbf{e}}_{1}},{{\mathbf{e}}_{2}},\cdots ,{{\mathbf{e}}_{{{M}^{2}}}} e1,e2,⋯,eM2 ,其信号子空间 Ω s = s p a n { e 1 , e 2 , ⋯ , e K } = s p a n { b ( θ 1 ) , b ( θ 2 ) , ⋯ , b ( θ K ) } {{\Omega }_{s}}=span\left\{ {{\mathbf{e}}_{1}},{{\mathbf{e}}_{2}},\cdots ,{{\mathbf{e}}_{K}} \right\}\text{=}span\left\{ \mathbf{b}\left( {{\theta }_{1}} \right),\mathbf{b}\left( {{\theta }_{2}} \right),\cdots ,\mathbf{b}\left( {{\theta }_{K}} \right) \right\} Ωs=span{e1,e2,⋯,eK}=span{b(θ1),b(θ2),⋯,b(θK)}和噪声子空间 Ω N = s p a n { e K + 1 , e K + 2 , ⋯ , e M 2 } {{\Omega }_{N}}=span\left\{ {{\mathbf{e}}_{K+1}},{{\mathbf{e}}_{K+2}},\cdots ,{{\mathbf{e}}_{{{M}^{2}}}} \right\} ΩN=span{eK+1,eK+2,⋯,eM2},利用信号子空间 Ω s {{\Omega }_{s}} Ωs和噪声子空间 Ω N {{\Omega }_{N}} ΩN的正交性,可以得到MUSIC-like的空间谱为 P ( θ ) = 1 ∥ b H ( θ ) E N ∥ 2 2 P\left( \theta \right)=\frac{1}{\left\| {{\mathbf{b}}^{H}}\left( \theta \right){{\mathbf{E}}_{N}} \right\|_{2}^{2}} P(θ)=∥bH(θ)EN∥221
其中 b ( θ ) = a ( θ ) ⊗ a ∗ ( θ ) \mathbf{b}\left( \theta \right)=\mathbf{a}\left( \theta \right)\otimes \mathbf{a}^*\left( \theta \right) b(θ)=a(θ)⊗a∗(θ), E N {{\mathbf{E}}_{N}} EN为噪声子空间, P ( θ ) P\left( \theta \right) P(θ)的 K K K个极大值点对应的角度位置即为DOA角度。Music-like 算法扩展阵列示意图如下

四、算法仿真
这里简单给出MUSIC-like算法和Music算法的对比,(基于四阶累积量的Music算法与MUSIC-like算法基本相同,这里就不再具体仿真,想仿真的只需要简单改下代码即可)
实验参数设置
| 参数名称 | 参数值 |
|---|---|
| 阵元数 | 5 |
| 阵元间距 | λ / 2 \lambda/2 λ/2 |
| 信源数目 | 3 |
| 信源角度 | θ 1 = − 40 , θ 2 = − 5 , θ 3 = 30 \theta_1=-40,\theta_2=-5,\theta_3=30 θ1=−40,θ2=−5,θ3=30 |
| 信噪比 | 10dB |
| 快拍数 | 512 |
在上述仿真条件下,给出两者的对比如下
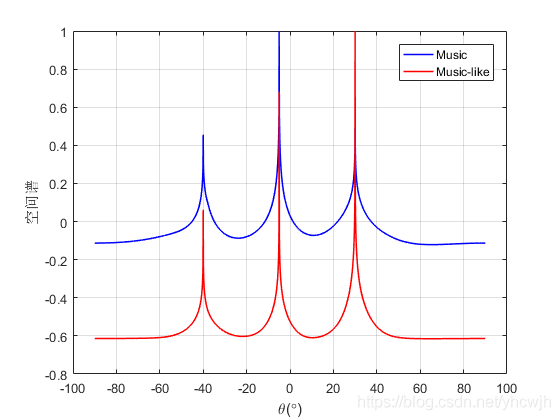
从图中可以看出,两者均能较好地区分出信号的DOA,同时将信源变成5个,此时的Music算法以及失效,但是由于Music-like算法的阵元扩展效果,依然能够分辨出信号的波达方向,其结果如下图所示
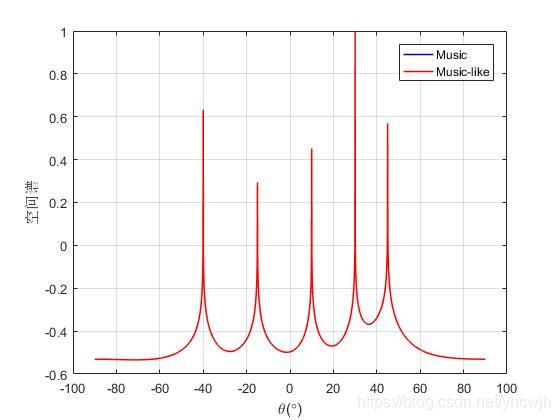
关于四阶累积量,其实有很多种定义,不同定义得到的结果可能不尽相同,文中只给出一种表示方法。同样地,也可以利用MATLAB高阶谱分析工具箱(HOSA)进行计算,这里就不再叙述
代码
clear;
close all;
clc;
derad = pi/180; % 角度变弧度
radeg = 180/pi; %弧度变角度
twpi = 2*pi; %2π
%%参数设置
M=5; %阵元数
snap=512; %信号长度、快拍数
dd=0.5; %阵元间距
d=0:dd:(M-1)*dd;
snr=10; %信噪比
K=5; %信源数
theta_range = 10;
% theta = (-theta_range:2*theta_range/(K-1):theta_range);
theta=[-40 -15 10 30 45]; %待估计的DOA
A=exp(-1i*twpi*d.'*sin(theta*derad)); %导向矢量矩阵
fs=pi/4; %产生非高斯信号的参数
w1=1:1/(K-1):2;
w=w1*fs;%信号频率
w=w.';
Pm1=0; %初始化MUSIC谱
Pm2=0; %初始化MUSIC-like谱
iter=10; %循环次数
for i=1:iter
for k=1:K %产生信号
r(k)=2*pi*randn(); %产生随机相位
S(k,:)=10^(snr/20)*exp(j*w(k)*[0:snap-1]+r(k));
end
noise=(randn(M,snap)+1i*randn(M,snap))*sqrt(0.5); %产生具有单位方差的噪声
X=A*S+noise; %产生阵列接收数据
Rxx=X*X'/snap; %协方差矩阵
[EV,D]=eig(Rxx); %特征值分解,从小到大
EVA=diag(D)'; %将特征值矩阵对角线提取并转为一行
[EVA,I]=sort(EVA); %将特征值排序 从小到大
EV=fliplr(EV(:,I)); % 对应特征矢量排序
En1=EV(:,K+1:M); % 取矩阵的第K+1到M列组成噪声子空间
%% MUSIC-LIKE 算法
C4=(kron(X,conj(X))*(kron(X,conj(X))'))/snap-kron(X,conj(X))/snap*kron(X,conj(X))'/snap-...
kron(X*X'/snap,conj(X*X'/snap)); % 四阶累积量计算
[V,D] = svd(C4); % 奇异值分解
En2 = V(:,K+1:M^2); % 噪声子空间
%%空间谱计算
ang=-90:0.1:90;
for ii=1:length(ang)
a=exp(-1j*twpi*d.'*sin(ang(ii)*derad));
Pmusic1(ii)=1/abs(a'*En1*En1'*a); %MUSIC谱
b = kron(a,conj(a)); % 扩展后的导向矢量
Pmusic2(ii)=1/abs(b'*En2*En2'*b);
end
Pm1=Pm1+10*log10(Pmusic1);
Pm2=Pm2+10*log10(Pmusic2);
end
Pm1=Pm1/iter;
Pm2=Pm2/iter;
Pm1=Pm1/max(Pm1);
Pm2=Pm2/max(Pm2);
figure(1);
plot(ang,Pm1,'b','linewidth',1.2);
hold on;
grid on;
plot(ang,Pm2,'r','linewidth',1.2);
xlabel('\theta(\circ)')
ylabel('空间谱')
legend('Music','Music-like');
参考文献:
[1]高阶统计量,百度百科
[2]高阶统计量,搜狗百科
[3]较为详细的MUSIC算法原理及MATLAB实现
[4]廖春艳. 基于二阶和高阶统计量DOA估计算法的对比[J]. 长沙大学学报, 2012(02):18-20.
[5]王静. 基于高阶累积量与稀疏约束的DOA估计方法[D]. 电子科技大学.
[6]朱敏,何培宇.一种新的基于四阶累积量的DOA估计算法[J].四川大学学报(自然科学版),2011,48(2):343-348.
[7]刁鸣,吴小强,李晓刚.基于四阶累积量的测向方法研究[J].系统工程与电子技术,2008,30(2):226-228.
[8]武思军,张锦中,张曙.基于四阶累积量进行阵列扩展的算法研究[J].哈尔滨工程大学学报,2005,26(3):394-397.