时间序列分解：stl、prophet原理与实现

参考文章：

局部加权线性回归Lowess
时间序列分解算法：STL
时间序列分解-STL分解法
STL——以鲁棒局部加权回归作为平滑方法的时间序列分解方法

STL时序分解：

将时序分解为趋势项、季节项（周、月等）、余项。利用Lowess局部加权回归技术进行平滑；通过外循环设计体现鲁棒性。

分别用Yv， Tv，Sv，Rv分别代表数据，趋势项、季节项和余项，v的范围为0到N，那么Yv=Tv+Sv+Rv ，其中v=1,⋯,N （加法模型中，各项具有相同量纲、STL只能处理加法模型，可以先将数据取对数，进行STL分解后的各分量结果取指数即可）

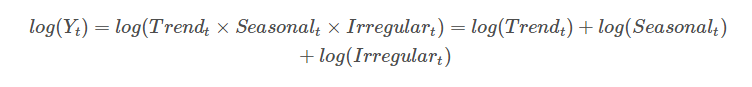
T(k)v、Sv(k)为内循环中第k-1次pass结束时的趋势分量、周期分量，初始时T(k)v=0
每个周期相同位置的样本点组成一个子序列（subseries），共有 n(pi)个子序列。

涉及参数：
• n(i) 内层循环数，一般为1-2
• n(o) 外层循环数， 一般不超过10；没有异常值时，可以设为0
• n(pi) 为一个周期的样本数（p在()中会显示乱码，用pi表示），
• n(s) 为Step 2中LOESS平滑参数，窗口大小，越大则子序列越平滑，一般不小于7的奇数
• n(l) 为Step 3中LOESS平滑参数，窗口大小，通常为大于等于n(pi)的最小奇数
• n(t)为Step 6中LOESS平滑参数，窗口大小，通常n(pi)—2n(pi)的奇数

内循环步骤：

Step 1: 去趋势（Detrending），减去上一轮结果的趋势分量T(k)v，即Yv−T(k)v

Step 2: 周期子序列平滑，用LOESS (q=n(s), d=1 )对每个子序列做回归，并向前向后各延展一个周期（单个子序列前后各延一个点）；平滑结果组成temporary seasonal series，记为C(k+1)v

Step 3: 周期子序列的低通量过滤，对上一个步骤的结果序列C(k+1)v依次做长度为n(pi)、n(pi)、3的滑动平均（moving average），然后做LOESS (q=n(l), d=1)回归，得到结果序列L(k+1)v,v=1,⋯,N ；相当于周期子序列的低通量L(k+1)v；

Step 4: 去除平滑周期子序列的低通量，得到季节项：S(k+1)v=C(k+1)v−L(k+1)v

Step 5: 去周期（Deseasonalizing），减去季节项分量，Yv−S(k+1)v

Step 6 : 趋势平滑（Trend Smoothing），对于step5中去除周期之后的序列做LOESS (q=n(t), d=1)回归，得到趋势分量T(k+1)v

外循环步骤：

计算更新各样本点v的鲁棒权重ρv值，在对应内循环的Step 2与Step 6中做LOESS回归时，邻域权重需要乘以ρv。
ρv值的计算：ρv=B(|Rv|/h)，其中，h=6∗median(|Rv|)

数据点的余项Rv越大，对应ρv权重越小；外循环主要用于调节robustness weight。如果数据序列中有异常值，则余项会较大，可以减小影响.

总结：

outer loop:
	计算robustness weight;
	inner loop:
		Step 1 去趋势：Yv−T(k)v;
		Step 2 周期子序列平滑：C(k+1)v;
		Step 3 周期子序列的低通量过滤：L(k+1)v;
		Step 4 去除平滑周期子序列趋势：S(k+1)v=C(k+1)v−L(k+1)v;
		Step 5 去周期：Yv−S(k+1)v;
		Step 6 趋势平滑：T(k+1)v;

X-11、STL、prophet方式时序分解的python实现

1.导入相关模块

statsmodels模块实现X-11时序分解；
rpy2模块实现对R语言相关模块STL的调用，另需要安装R软件；
fbprophet 模块实现prophet分解。

"""
安装R软件后，需要定义相关环境变量，或者直接添加如下三行定义，路径为R软件安装位置
如果出现cannot load library R.dll的错误，尝试卸载rpy2模块，移步‘https://www.lfd.uci.edu/~gohlke/pythonlibs/’网页下载非官方rpy2模块
Prophet安装失败可参考"https://www.it1352.com/2129684.html"
holidays功能需要pandas version <1.1.0 (e.g. 1.0.5)
"""
import os
# os.environ['R_HOME']='D:/Program Files/R/R-4.0.3'
# os.environ['PATH'] += os.pathsep + 'D:/Program Files/R/R-4.0.3/bin/X64/'
# os.environ['PATH'] += os.pathsep + 'D:/Program Files/R/R-4.0.3/'
import rpy2.robjects as robjects
from rpy2.robjects import pandas2ri
from rpy2.robjects import r
import statsmodels.api as sm
from fbprophet import Prophet

import seaborn as sns
import matplotlib.pyplot as plt
import math
import numpy as np
import pandas as pd
from pandas import DataFrame

2.利用statsmodels模块的seasonal_decompose函数实现X-11时序分解（非STL分解）

2.1算法实现函数decompose_x11如下：

def decompose_x11(dta, freq):
    """
    算法二：
    利用statsmodels模块的seasonal_decompose函数实现X-11时序分解（非STL分解）
    dta:预测数据，含'timestamp','value'两列
    """
    dta = dta.set_index('timestamp')
    dta['value'] = dta['value'].apply(pd.to_numeric, errors='ignore')
    dta.value.interpolate(inplace=True)
    """
    seasonal_decompose函数参数说明：
    model："additive"为加法模型， "multiplicative"为乘法模型
    freq:指定序列周期
    """
    res = sm.tsa.seasonal_decompose(dta.value, freq=freq, model="additive")
    trend = res.trend
    seasonal = res.seasonal
    residual = res.resid
    # 分解模型展示
    # res.plot()
    # plt.show()

    return trend, seasonal, residual

2.2具体实例的相关说明，另两种算法实现参考本实例

实例数据说明：'report_date_level_3to8.csv’含两列：时间列和待预测时序列；

先进行周期7day的分解，对结果趋势项、随机项合并进行周期30day的二次分解；

add2mult函数：实现加法模型的乘法分解（将df数据取对数，进行加法分解，然后将分项取指数即可）。

"""
先对数据进行周期为7 day的分解，得到T_1、S_7、R_1项；
将T_1、R_1合并(乘法模型中的合并为乘)进行周期为30 day的分解,得到T_2、S_30、R_2项，即原始数据由T_2、S_7、S_30、R_2组成；
如何考虑节假日的影响，根据上述R_2值（历史节假日）进行修正。
具体步骤如下：
step1:待预测数据data取对数，得到log(data）
step2：对log(data）进行加法分解（频率为7），并将得到的三分项取指数运算，得到T_1、S_7、R_1
step3：T_1、R_1合并，取对数，进行加法分解（频率为30），并将得到的三分项取指数运算，得到T_2、S_30、R_2
step4：原始数据data由T_2、S_7、S_30、R_2的乘法模型组成，根据R_2值（历史节假日）进行修正
"""
# 获取purchase列的数据,并对列重命名
purchase_data = pd.read_csv('report_date_level_3to8.csv', usecols=[1, 2])
purchase_data = purchase_data.rename(columns={'report_date':'timestamp', 'total_purchase_amtsum':'value'})


def add2mult(df, sea_freq, decompose_type=decompose_x11):
    """
    # 定义一个函数，实现乘法模型与加法模型的转变,即实现上述step1和step2
    data：待处理数据，含'timestamp'，'value'两列
    sea_freq：时序分解周期
    decompose_type：时序分解方式，x11或stl
    返回分解之后的各项T、S、R，各项之间是相乘的关系，但是用到的分解模型是加法模型
    """
    data = df.copy(deep=True)
    """step1: 待预测数据data取对数"""
    data['value'] = data['value'].apply(lambda x: math.log(x))
    """step2"""
    trend, seasonal, residual = decompose_type(data, sea_freq)
    # 将分解得到的三项由series转化为dataframe数据类型
    T_1 = pd.DataFrame({'timestamp': trend.index, 'value': trend.values})
    S_7 = pd.DataFrame({'timestamp': seasonal.index, 'value': seasonal.values})
    R_1 = pd.DataFrame({'timestamp': residual.index, 'value': residual.values})
    # 首位NAN的填充(X-11时序分解得到的trend、residual的前后半个周期均为空值，对空值用最近的非空值替代)
    if decompose_type == decompose_x11:
        m = T_1.shape[0]
        T_1.iloc[:int(sea_freq/2.0), 1].fillna(T_1.iloc[int(sea_freq/2.0)][1], inplace=True)
        T_1.iloc[m-int(sea_freq/2.0):, 1].fillna(T_1.iloc[m-int(sea_freq/2.0)-1]['value'], inplace=True)
        R_1.iloc[:int(sea_freq/2.0), 1].fillna(R_1.iloc[int(sea_freq/2.0)][1], inplace=True)
        R_1.iloc[m-int(sea_freq/2.0):, 1].fillna(R_1.iloc[m-int(sea_freq/2.0)-1]['value'], inplace=True)
    # 取指数运算
    T_1['value'] = T_1['value'].apply(lambda x: math.exp(x))
    S_7['value'] = S_7['value'].apply(lambda x: math.exp(x))
    R_1['value'] = R_1['value'].apply(lambda x: math.exp(x))

    return T_1, S_7, R_1

2.3 具体x11时序分解实例代码

x11分解的结果，因取移动平均算法，trend和residual 分项会有前后半周期缺失，进行最近非nan值填充，在上述add2mult函数有体现

"""利用X-11算法对数据进行多周期时序分解(T、R首位半周期缺失)"""
# 周期为7的分解，得到T_1, S_7, R_1
T_1, S_7, R_1 = add2mult(purchase_data, 7, decompose_type=decompose_x11)
# 对T_1、R_1合并（相乘），得到TR_1
TR_1 = T_1.copy(deep=True)
TR_1['value'] = T_1['value'] * R_1['value']
# 周期为30的分解，得到T_2, S_30, R_2
T_2, S_30, R_2 = add2mult(TR_1, 30, decompose_type=decompose_x11)
# 原始数据data由T_2、S_7、S_30、R_2的乘法模型组成，根据R_2值（历史节假日）进行修正
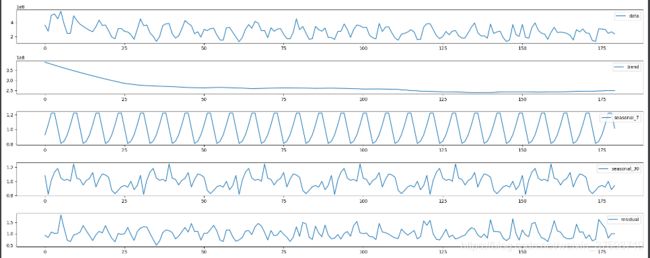
plt.figure(figsize=(20, 8))
plt.subplot(511)
plt.plot(purchase_data['value'], label="data")
plt.legend()
plt.subplot(512)
plt.plot(T_2['value'], label="trend")
plt.legend()
plt.subplot(513)
plt.plot(S_7['value'], label="seasonal_7")
plt.legend()
plt.subplot(514)
plt.plot(S_30['value'], label="seasonal_30")
plt.legend()
plt.subplot(515)
plt.plot(R_2['value'], label="residual")
plt.legend()
plt.show()

结果分解如下图：

3 利用rpy2模块实现对R语言stl函数的调用，进行STL时序分解

3.1算法实现函数如下：

def decompose_stl(df, frequency, s_window="periodic", **kwargs):
    """算法一：利用rpy2模块实现对R语言stl函数的调用，进行STL时序分解"""
    s = df['value'].tolist()
    length = df.shape[0]
    s = r.ts(s, frequency=frequency)
    """
    R语言stl函数参数说明：
    stl(x, 
    s.window,                           # 提取季节分量时的loess平滑窗口大小；"periodic"可使得季节效应在各年间都一样
    s.degree = 0,                       # 提取季节分量时的loess平滑拟合多项式阶数，0或1
    t.window = NULL,                    # 提取趋势分量时的loess平滑窗口大小
    t.degree = 1,                       # t.degree有时需要写成d_degree或t_degree
    l.window = nextodd(period), 
    l.degree = t.degree,
    s.jump = ceiling(s.window/10),
    t.jump = ceiling(t.window/10),
    l.jump = ceiling(l.window/10),
    robust = FALSE,                     # 是否启用鲁棒性
    inner = if(robust)  1 else 2,       # 内循环次数
    outer = if(robust) 15 else 0,       # 外循环次数，如果不启用robust，则无外循环
    na.action = na.fail)
    """
    decomposed = [x for x in r.stl(s, s_window, **kwargs).rx2('time.series')]
    df['trend'] = decomposed[length:2*length]
    df['seasonal'] = decomposed[0:length]
    df['residual'] = decomposed[2*length:3*length]

    return df['trend'], df['seasonal'], df['residual']

3.2 具体stl时序分解实例代码：

具体实例数据，两次周期分解逻辑、add2mult函数实现参考2.2小节

"""利用STL算法对数据进行多周期时序分解"""
# 周期为7的分解，得到T_1, S_7, R_1
T_1, S_7, R_1 = add2mult(purchase_data, 7, decompose_type=decompose_stl)
# 对T_1、R_1合并（相乘），得到TR_1
TR_1 = T_1.copy(deep=True)
TR_1['value'] = T_1['value'] * R_1['value']
# 周期为30的分解，得到T_2, S_30, R_2
T_2, S_30, R_2 = add2mult(TR_1, 30, decompose_type=decompose_stl)
# 原始数据data由T_2、S_7、S_30、R_2的乘法模型组成，根据R_2值（历史节假日）进行修正
plt.figure(figsize=(20, 8))
plt.subplot(511)
plt.plot(purchase_data['value'], label="data")
plt.legend()
plt.subplot(512)
plt.plot(T_2['value'], label="trend")
plt.legend()
plt.subplot(513)
plt.plot(S_7['value'], label="seasonal_7")
plt.legend()
plt.subplot(514)
plt.plot(S_30['value'], label="seasonal_30")
plt.legend()
plt.subplot(515)
plt.plot(R_2['value'], label="residual")
plt.legend()
plt.show()

分解结果如下：

4 利用fbprophet模块实现时序分解（类似STL分解）

"""
算法三：调用脸书的Prophet算法进行时序分解(加法或乘法模型可选)，类似于STL算法
"""

df = purchase_data.copy(deep=True)
df = df.rename(columns={'timestamp':'ds', 'value':'y'})      # 将数据df的两列名称timestamp、value改为ds、y
# df['y'] = (df['y'] - df['y'].mean()) / (df['y'].std())     # 时间序列需要进行归一化的操作
"""
Prophet参数介绍：
growth='linear',                   增长函数,如果要是用逻辑回归函数的时候，需要设置 capacity 的值
changepoints=None,
n_changepoints=25,
changepoint_range=0.8,
yearly_seasonality='auto',         周期设置
weekly_seasonality='auto',
daily_seasonality='auto',
holidays=None,                     节假日设置
seasonality_mode='additive',       加法模型与乘法模型
seasonality_prior_scale=10.0,
holidays_prior_scale=10.0,         类似节假日权重，越大则节假日权重越大
changepoint_prior_scale=0.05,
mcmc_samples=0,
interval_width=0.80,
uncertainty_samples=1000
"""
# 节假日前后影响范围，也就是 lower_window 和 upper_window
playoffs = pd.DataFrame({
  'holiday': 'playoff',
  'ds': pd.to_datetime(['2014-04-05', '2014-04-06', '2014-04-07',
                        '2014-05-01', '2014-05-02', '2014-05-03',
                        '2014-05-31', '2014-06-01', '2014-06-02',
                        '2014-09-06', '2014-09-07', '2014-09-08',
                        '2014-10-01', '2014-10-02', '2014-10-03', '2014-10-04', '2014-10-05',
                        '2014-10-06', '2014-10-07']),
  'lower_window': 0,
  'upper_window': 1,
})

superbowls = pd.DataFrame({
  'holiday': 'superbowl',
  'ds': pd.to_datetime(['2014-10-01', '2014-10-02', '2014-10-03', '2014-10-04', '2014-10-05',
                        '2014-10-06', '2014-10-07']),
  'lower_window': 0,
  'upper_window': 1,
})
holidays = pd.concat((playoffs, superbowls))

# df['cap'] = df['y'].apply(lambda x: 1000000000)
# df['cap'] = 1000000000

# 初始化模型
m = Prophet(seasonality_mode='multiplicative',
            holidays=holidays, holidays_prior_scale=1.0,
            weekly_seasonality=True)  
# 添加季节特征
m.add_seasonality(name='weekly', period=7, fourier_order=3, prior_scale=0.1)  # fourier_order:类似于平滑窗口，但是取值越小则曲线越平滑
m.add_seasonality(name='monthly', period=30, fourier_order=5)

# 拟合模型
m.fit(df)                                                  

future = m.make_future_dataframe(periods=0)   # 计算预测值：periods 表示需要预测的点数，freq 表示时间序列的频率
future.tail()
forecast = m.predict(future)
# # 画出预测图
# m.plot(forecast)
# plt.show()
# # 画出时间序列的分量图
# m.plot_components(forecast)
# plt.show()


# forecast['yhat']  = forecast['trend'] * forecast['weekly'] * forecast['monthly'] * forecast['holidays']

# 作图
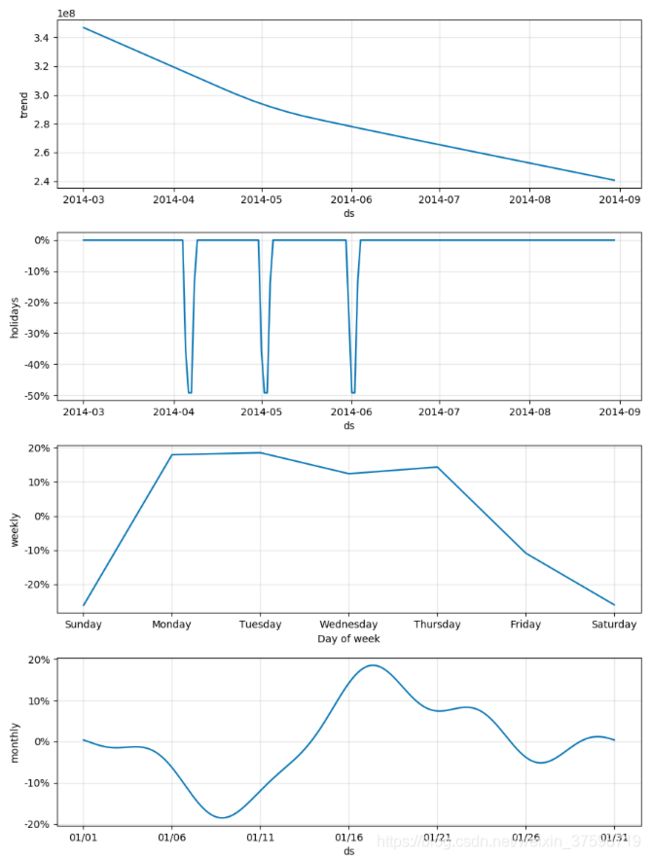
plt.figure(figsize=(20, 8))
plt.subplot(511)
plt.plot(forecast['yhat'], label="data")
plt.legend()
plt.subplot(512)
plt.plot(forecast['trend'], label="trend")
plt.legend()
plt.subplot(513)
plt.plot(forecast['weekly'], label="seasonal_7")
plt.legend()
plt.subplot(514)
plt.plot(forecast['monthly'], label="seasonal_30")
plt.legend()
plt.subplot(515)
plt.plot(forecast['holidays'], label="holidays")
plt.legend()
plt.show()

prophet模块作图、原始data与各分量对比，分别如下：

谢谢阅读！