数据结构与算法-二叉树
数据结构与算法-二叉树
- 1 二叉树的基本结构
- 2 二叉树的递归遍历
-
- 2.1 递归前序遍历
- 2.2 递归中序遍历
- 2.3 递归后序遍历
- 3 二叉树的非递归遍历
-
- 3.1 非递归前序遍历
- 3.2 非递归中序遍历
- 3.3 非递归后序遍历
- 3.4 leetcode 题目
- 4 二叉树的宽度优先遍历
- 5 求二叉树的最大宽度
- 6 判断一棵二叉树是否是搜索二叉树
- 7 判断一棵二叉树是否是完全二叉树
- 8 判断一棵树是否是满二叉树
- 9 判断一棵二叉树是否是平衡二叉树
- 10 公共祖先问题
- 11 二叉树的层序遍历
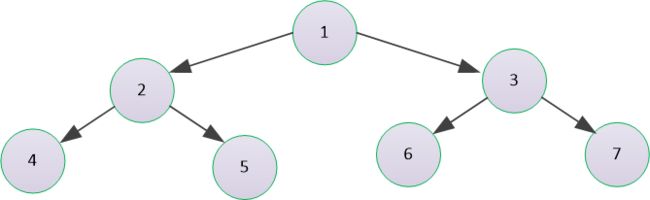
1 二叉树的基本结构
public static class TreeNode {
int val;
TreeNode left; // 左子节点
TreeNode right;// 右子节点
TreeNode(int val){
this.val = val;
}
}
2 二叉树的递归遍历
2.1 递归前序遍历
输出当前节点 → \rightarrow → 输出左子节点 → \rightarrow → 输出右子节点
coding
/**
* 二叉树的前序遍历
* @param root
*/
public static void preOrderRecur(TreeNode root){
if (root == null){
return;
}
System.out.print(root.val + " ");
preOrderRecur(root.left);
preOrderRecur(root.right);
}
二叉树基本结构中的二叉树使用前序遍历输出节点如下 :
1 → \rightarrow → 2 → \rightarrow → 4 → \rightarrow → 5 → \rightarrow → 3 → \rightarrow → 6 → \rightarrow → 7
2.2 递归中序遍历
coding
public static void inOrderRecur(TreeNode root){
if (root == null){
return;
}
inOrderRecur(root.left);
System.out.println(root.val + " ");
inOrderRecur(root.right);
}
二叉树基本结构中的二叉树使用中序遍历输出节点如下 :
4 → \rightarrow → 2 → \rightarrow → 5 → \rightarrow → 1 → \rightarrow → 6 → \rightarrow → 3 → \rightarrow → 7
输出左子节点 → \rightarrow → 输出父节点 → \rightarrow → 输出右子节点
2.3 递归后序遍历
coding
public static void posOrderRecur(TreeNode root){
if (root == null){
return;
}
posOrderRecur(root.left);
posOrderRecur(root.right);
System.out.print(root.val + " ");
}
二叉树基本结构中的二叉树使用后序遍历输出节点如下 :
4 → \rightarrow → 5 → \rightarrow → 2 → \rightarrow → 6 → \rightarrow → 7 → \rightarrow → 3 → \rightarrow → 1
二叉树的递归遍历使用了递归调用的栈机制
3 二叉树的非递归遍历
3.1 非递归前序遍历
/**
* 二叉树 前序遍历 非递归方式
* @param root
*/
public static void preOrderNonRecur(TreeNode root){
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
root = stack.pop();
System.out.print(root.val + " ");
if (root.right != null){
stack.push(root.right);
}
if (root.left != null){
stack.push(root.left);
}
}
}
3.2 非递归中序遍历
/**
* 二叉树的中序遍历 非递归方式
* @param root
*/
public static void inOrderNonRecur(TreeNode root){
if (root == null){
return;
}
Stack<TreeNode> stack = new Stack<>();
while (!stack.isEmpty() || root != null){
if (root != null){
stack.push(root);
root = root.left;
} else { // 节点的左子节点为空
// 从栈中弹出一个
root = stack.pop();
System.out.println(root.val + " ");
// 右边节点进栈
root = root.right;
}
}
}
3.3 非递归后序遍历
public static void posOrderUnRecur(TreeNode root){
if (root == null){
return;
}
Stack<TreeNode> s1 = new Stack<>();
Stack<TreeNode> s2 = new Stack<>();
s1.push(root);
while (!s1.isEmpty()){
root = s1.pop();
s2.push(root);
// 左边先进栈
if (root.left != null){
s1.push(root);
}
// 右边进栈
if (root.right != null){
s1.push(root);
}
}
while (!s2.isEmpty()){
System.out.println(s2.pop().val + " ");
}
}
3.4 leetcode 题目
- 给你二叉树的根节点 root ,返回它节点值的前序遍历。
数据范围:二叉树的节点数量满足 1 ≤ n ≤ 100 1≤n≤100 1≤n≤100 ,二叉树节点的值满足 1 ≤ v a l ≤ 100 1≤val≤100 1≤val≤100 ,树的各节点的值各不相同
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型一维数组
*/
public int[] preorderTraversal (TreeNode root) {
// write code here
if(root == null){
return null;
}
List<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()){
root = stack.pop();
list.add(root.val);
// 前序遍历 右边先进栈
if(root.right != null){
stack.push(root.right);
}
// 左边进栈
if(root.left != null){
stack.push(root.left);
}
}
int[] retArr = new int[list.size()];
for(int i = 0;i < list.size();++i){
retArr[i] = list.get(i);
}
return retArr;
}
- 给定一个二叉树的根节点root,返回它的中序遍历结果。
数据范围:树上节点数满足 0 ≤ n ≤ 1000 0≤n≤1000 0≤n≤1000,树上每个节点的值满足 − 1000 ≤ v a l ≤ 1000 −1000≤val≤1000 −1000≤val≤1000
进阶:空间复杂度 O ( n ) O(n) O(n),时间复杂度 O ( n ) O(n) O(n)
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型一维数组
*/
public int[] inorderTraversal (TreeNode root) {
// write code here
if (root == null){
return new int[0];
}
Stack<TreeNode> stack = new Stack<>();
List<Integer> list = new ArrayList<>();
while(!stack.isEmpty() || root != null){
if(root != null){
stack.push(root);
root = root.left;
} else {
root = stack.pop();
list.add(root.val);
root = root.right;
}
}
int[] resArr = new int[list.size()];
for(int i = 0;i < list.size();i++){
resArr[i] = list.get(i);
}
return resArr;
}
- 给定一个二叉树,返回他的后序遍历的序列。
后序遍历是值按照 左节点->右节点->根节点 的顺序的遍历。
数据范围:二叉树的节点数量满足 1 ≤ n ≤ 100 1≤n≤100 1≤n≤100,二叉树节点的值满足 1 ≤ v a l ≤ 100 1≤val≤100 1≤val≤100 ,树的各节点的值各不相同
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型一维数组
*/
public int[] postorderTraversal (TreeNode root) {
// write code here
if(root != null){
Stack<TreeNode> s1 = new Stack<>();
Stack<TreeNode> s2 = new Stack<>();
List<Integer> list = new ArrayList<>();
s1.push(root);
while(! s1.isEmpty()){
root = s1.pop();
s2.push(root);
// 左边先进第一个栈s1 然后边后出第一个栈s1 后入s2 先出s2
if(root.left != null){
s1.push(root.left);
}
if(root.right != null){
s1.push(root.right);
}
}
while(!s2.isEmpty()){
list.add(s2.pop().val);
}
int[] retArr = new int[list.size()];
for(int i = 0; i < list.size();++i){
retArr[i] = list.get(i);
}
return retArr;
}
return new int[0];
}
}
4 二叉树的宽度优先遍历
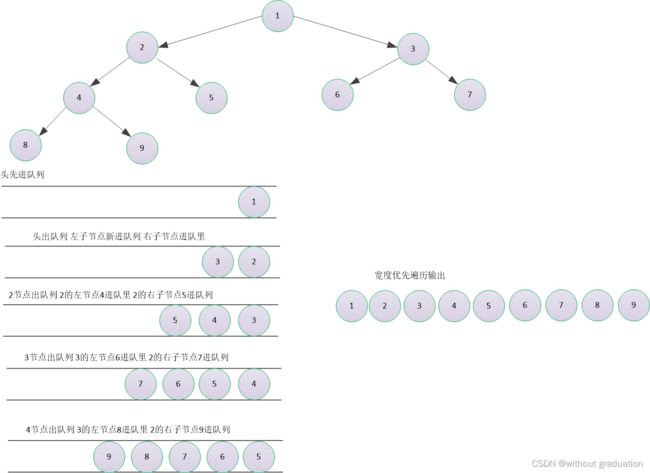
遍历方法及步骤
使用队列,头先进队列,从头里面取出一个节点,然后左子节点先进队列,然后右子节点进队列,周而复始,直到队列为空
二叉树宽度优先遍历图解如 :
coding
/**
* 二叉树的宽度优先遍历
* @param root
*/
public static void widthFirstTraversal(TreeNode root){
if (root == null){
return;
}
// 队列 双向链表可以当做队列
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
// 从队里中取出一个节点 取出就打印
root = queue.poll();
System.out.print(root.val + " ");
if (root.left != null){
queue.add(root.left);
}
if (root.right != null){
queue.add(root.right);
}
}
System.out.println();
}
5 求二叉树的最大宽度
使用宽度优先遍历,计算出每一层的节点个数,每来到一个新的层,就计算一次最大的节点个数
/**
* 求二叉树的最大宽度
* @param root
* @return
*/
public static int getMaxWidth(TreeNode root){
if (root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
// 每一个节点所在的层
Map<TreeNode,Integer> nodeMap = new HashMap<>();
// 根节点在第一层
nodeMap.put(root,1);
// 当前层的节点数
int curLevelNodeCnt = 0;
// 当前所在的层
int curLevel = 1;
// 最大的节点个数
int maxNodeCnt = -1;
while (!queue.isEmpty()){
root = queue.poll();
// 还在当前层
if (nodeMap.get(root) == curLevel){
// 当前层的节点个数加1
curLevelNodeCnt ++;
} else { // 来到了下一层
// 求最大的节点个数
maxNodeCnt = Math.max(curLevelNodeCnt,maxNodeCnt);
// 当前来到下一层 当前层的节点个数为 1
curLevelNodeCnt = 1;
curLevel ++;
}
if (root.left != null) {
// 节点所在的层
nodeMap.put(root.left,curLevel + 1);
queue.add(root.left);
}
if (root.right != null){
nodeMap.put(root.right,curLevel + 1);
queue.add(root.right);
}
}
return maxNodeCnt;
}
不使用hashMap求二叉树的最大宽度
使用两个变量当前层的结束节点 curEndNode 下一层的结束节点 nextEndNode
整个过程如图所示 :

coding
public static int getMaxWidthNoMap(TreeNode root){
if (root == null){
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
TreeNode curEndNode = root;//当前层的最后一个节点
TreeNode nextEndNode = null;// 下一层的最后一个节点
int curLevelNodeCnt = 1;
int maxNodeCnt = -1;
while (!queue.isEmpty()){
TreeNode cur = queue.poll();
if (cur.left != null){
queue.add(cur.left);
nextEndNode = cur.left;
}
if (cur.right != null){
queue.add(cur.right);
nextEndNode = cur.right;
}
// 当前节点是最后一个节点
if (cur == curEndNode){
maxNodeCnt = Math.max(curLevelNodeCnt,maxNodeCnt);
curEndNode = nextEndNode;
nextEndNode = null;
// 要把当前层的最后一个节点算上 所以 curLevelNodeCnt置1
curLevelNodeCnt = 1;
} else { // 不是最后一个节点
curLevelNodeCnt ++;
}
}
return maxNodeCnt;
}
6 判断一棵二叉树是否是搜索二叉树
使用中序遍历的方式判断
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public static int preVal = Integer.MIN_VALUE;
public boolean isValidBST (TreeNode root) {
// write code here
if (root == null) {
return true;
}
boolean isLeftBst = isValidBST(root.left);
// 左边不是搜索二叉树 直接返回
if (!isLeftBst) {
return false;
}
if (root.val <= preVal) {
return false;
} else {
preVal = root.val;
}
return isValidBST(root.right);
}
}
使用非递归方式进行判断
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public boolean isValidBST (TreeNode root) {
// write code here
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
int preVal = Integer.MIN_VALUE;
while (!stack.isEmpty() || root != null ) {
//左边进栈
if (root != null) {
stack.push(root);
root = root.left;
} else { // 弹出节点 右边界进栈
root = stack.pop();
if (root.val <= preVal) {
return false;
} else {
preVal = root.val;
}
root = root.right;
}
}
return true;
}
}
使用递归套路求判断二叉树是否是搜索二叉树
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public class ReturnData {
public boolean isBST;
public int min;
public int max;
public ReturnData( boolean isBST, int min, int max) {
this.isBST = isBST;
this.min = min;
this.max = max;
}
}
public boolean isValidBST (TreeNode root) {
// write code here
return process(root).isBST;
}
public ReturnData process(TreeNode root) {
if (root == null) {
return null;
}
// 获取左侧数据
ReturnData leftData = process(root.left);
// 获取右侧数据
ReturnData rightData = process(root.right);
boolean isBST = true;
int min = root.val;
int max = root.val;
if (leftData != null) {
min = Math.min(leftData.min, min);
max = Math.max(leftData.max, max);
// 左侧已经不是二叉树 或者左子树的最大值大于等于当前节点的值 则不是搜素二叉树
if (!leftData.isBST || (leftData.max >= root.val)) {
isBST = false;
}
}
if (rightData != null) {
min = Math.min(rightData.min, min);
max = Math.max(rightData.max, max);
if (! rightData.isBST || (rightData.min <= root.val)) {
isBST = false;
}
}
return new ReturnData(isBST,min,max);
}
}
7 判断一棵二叉树是否是完全二叉树
关于什么是完全二叉树可以看博主文章
数据结构与算法之排序算法 堆排序节
使用宽度优先进行遍历,在遍历的过程中如果遇到如下情况 :
- 有右子节点,但是没有左子节点 直接返回
false - 在1)不违规的条件下,如果遇到了左右子节点不双全的情况,接下来的所有节点必须是叶子节点,否则就不是完全为二叉树
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return bool布尔型
*/
public boolean isCompleteTree (TreeNode root) {
// write code here
if (root == null) {
return true;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
boolean isLeaf = false;
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
TreeNode left = cur.left;
TreeNode right = cur.right;
// 当前节点有右子节点 但是没有左子节点
if (left == null && right != null) {
return false;
}
// 如果已经遇到了叶子节点 后面还是出现了非叶子节点 则不是完全二叉树
if (isLeaf && (left != null || right != null)) {
return false;
}
// 如果之前没有遇到过叶子节点 需要判断一下当前节点是否只有一个节点
// 如果只有一个 则是叶子节点
if (!isLeaf && (left == null || right == null)) {
isLeaf = true;
}
if (left != null) {
queue.add(left);
}
if (right != null) {
queue.add(right);
}
}
return true;
}
}
8 判断一棵树是否是满二叉树
二叉树的节点个数n和二叉树h的高度满足如下关系 :
n = 2 h − 1 n = 2 ^ h - 1 n=2h−1
coding
public static class Info{
int height;
int nodesCount;
public Info (int height,int nodesCount){
this.height = height;
this.nodesCount = nodesCount;
}
}
public static boolean isFullTree(TreeNode root){
Info info = process(root);
// 二叉树节点的个数与 二叉树的高度满足关系 N = 2^h - 1
return info.nodesCount == 1 << info.height - 1;
}
public static Info process(TreeNode root){
if (root == null){
return new Info(0,0);
}
Info leftInfo = process(root.left);
Info rightInfo = process(root.right);
int height = Math.max(leftInfo.height,rightInfo.height) + 1;
int nodesCount = leftInfo.nodesCount + rightInfo.nodesCount + 1;
return new Info(height,nodesCount);
}
9 判断一棵二叉树是否是平衡二叉树
平衡二叉树: 左树和右树的高度差不超过1
leetcode题目
描述
输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。
在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
/**
* 判断一棵树是否是平衡二叉树
* @param root
* @return
*/
public static boolean isBalanceTree(TreeNode root){
return process(root).isBalance;
}
public static ReturnData process(TreeNode root){
if (root == null){
return new ReturnData(true,0);
}
// 左树返回数据 : 左树的高度 左树是否是平衡二叉树
ReturnData leftData = process(root.left);
// 右树返回数据 : 右树的高度 右树是否是平衡二叉树
ReturnData rightData = process(root.right);
int height = Math.max(leftData.height,rightData.height) + 1;
boolean isBalance = leftData.isBalance && rightData.isBalance &&
Math.abs(leftData.height - rightData.height) < 2;
return new ReturnData(isBalance,height);
}
public static class ReturnData{
public boolean isBalance;//是否是平衡二叉树
public int height;//树的高度
public ReturnData(boolean isBalance,int height){
this.isBalance = isBalance;
this.height = height;
}
}
10 公共祖先问题
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @param p int整型
* @param q int整型
* @return int整型
*/
public int lowestCommonAncestor (TreeNode root, int p, int q) {
// write code here
// 每个节点的及其父节点放在Map中
// key 每个节点 value 每个节点的父节点
Map<Integer, Integer> parentMap = new HashMap<>();
parentMap.put(root.val, root.val);
process(root, parentMap);
Set<Map.Entry<Integer, Integer>> entries = parentMap.entrySet();
for (Map.Entry<Integer, Integer> entry : entries) {
System.out.println(entry.getKey() + " : " + entry.getValue());
}
Set<Integer> set = new HashSet<>();
set.add(root.val);
int cur1 = p;
int cur2 = q;
// n1一直往上蹿
while (cur1 != parentMap.get(cur1)) {
set.add(cur1);
cur1 = parentMap.get(cur1);
}
while (cur2 != parentMap.get(cur2)) {
if (set.contains(cur2)) {
return cur2;
}
cur2 = parentMap.get(cur2);
}
return root.val;
}
/**
* 设置每个节点及其父节点进 HashMap
* @param root
* @param parentMap
*/
public static void process(TreeNode root, Map<Integer, Integer> parentMap) {
if (root == null) {
return;
}
if (root.right != null) {
parentMap.put(root.right.val, root.val);
}
if (root.left != null) {
parentMap.put(root.left.val, root.val);
}
process(root.left, parentMap);
process(root.right, parentMap);
}
}
11 二叉树的层序遍历
给定一个二叉树,返回该二叉树层序遍历的结果,(从左到右,一层一层地遍历)
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param root TreeNode类
* @return int整型ArrayList>
*/
public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
// write code here
ArrayList<ArrayList<Integer>> arrayLists = new ArrayList<>();
if (root == null) {
return arrayLists;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
ArrayList<Integer> list = new ArrayList<>();
// 当前层的节点个数
int count = queue.size();
// 会把下一层的所有元素都放在队列中
while (count-- > 0) {
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
arrayLists.add(list);
}
return arrayLists;
}
}