Leetcode刷题笔记--Hot41-50

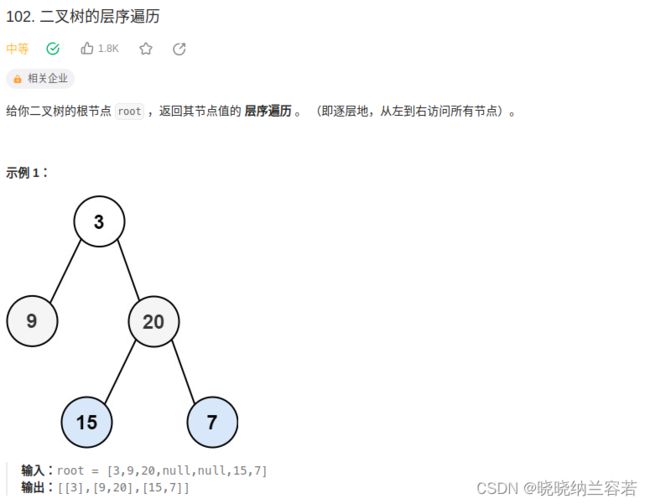
1--二叉树的层序遍历（102）

主要思路：

        经典广度优先搜索，基于队列；

        对于本题需要将同一层的节点放在一个数组中，因此遍历的时候需要用一个变量 nums 来记录当前层的节点数，即 nums 等于队列元素的数目；

#include 
#include 
#include 
 
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
 
class Solution {
public:
    std::vector> levelOrder(TreeNode* root) {
        std::vector> res;
        if(root == nullptr) return res;
        std::queue q;
        q.push(root);
        while(!q.empty()){
            int nums = q.size(); // 当前层的节点数
            std::vector tmp;
            while(nums > 0){ // 遍历处理同一层
                TreeNode *cur = q.front();
                q.pop();
                tmp.push_back(cur->val);
 
                if(cur->left != nullptr) q.push(cur->left);
                if(cur->right != nullptr) q.push(cur->right);
                
                nums--;
            }
            res.push_back(tmp); // 记录当前层的元素
        }
        return res;
    }
};
 
int main(int argc, char* argv[]){
    // root = [1, null, 2, 3]
    TreeNode *Node1 = new TreeNode(3);
    TreeNode *Node2 = new TreeNode(9);
    TreeNode *Node3 = new TreeNode(20);
    TreeNode *Node4 = new TreeNode(15);
    TreeNode *Node5 = new TreeNode(7);
    Node1->left = Node2;
    Node1->right = Node3;
    Node3->left = Node4;
    Node3->right = Node5;
 
    Solution S1;
    std::vector> res = S1.levelOrder(Node1);
    for(auto item : res) {
        for (int v : item) std::cout << v << " ";
        std::cout << std::endl;
    }
    return 0;
}

2--二叉树的最大深度（104）

主要思路：

        递归计算左右子树的深度，选取两者最大值 +1 返回；

#include 
#include 
#include 
 
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
 
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr) return 0;
        int res = dfs(root);
        return res;
    }
 
    int dfs(TreeNode* root){
        if(root == nullptr) return 0;
        int left_height = dfs(root->left);
        int right_height = dfs(root->right);
        int cur_height = std::max(left_height, right_height) + 1;
        return cur_height;
    }
};
 
int main(int argc, char* argv[]){
    // root = [3,9,20,null,null,15,7]
    TreeNode *Node1 = new TreeNode(3);
    TreeNode *Node2 = new TreeNode(9);
    TreeNode *Node3 = new TreeNode(20);
    TreeNode *Node4 = new TreeNode(15);
    TreeNode *Node5 = new TreeNode(7);
 
    Node1->left = Node2;
    Node1->right = Node3;
    Node3->left = Node4;
    Node3->right = Node5;
 
    Solution S1;
    int res = S1.maxDepth(Node1);
    std::cout << res << std::endl;
    return 0;
}

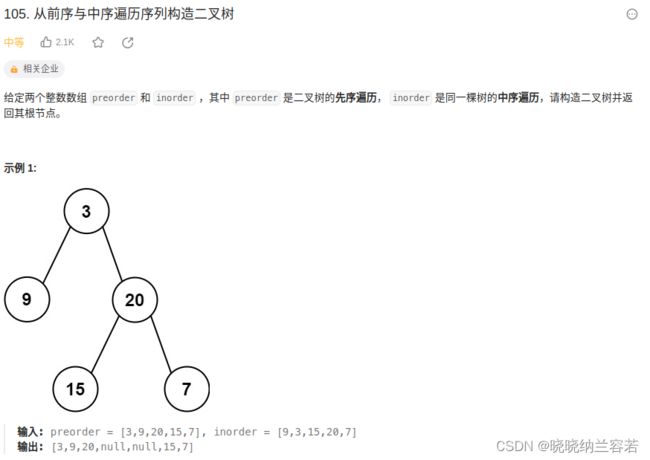
3--从前序与中序遍历序列构造二叉树（105）

主要思路：

        思路类似于根据中序和后序遍历来构建二叉树；

        对于本题，前序遍历的顺序是：根→左→右，则前序遍历的第一个节点是根节点；

        中序遍历的顺序是：左→根→右，遍历中序数组找到根节点的位置，根据根节点的位置划分左右子树；

        根据左右子树的大小划分前序遍历得到前序遍历的左右子树，递归构建左右子树即可；

#include 
#include 
#include 

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* buildTree(std::vector& preorder, std::vector& inorder) {
        TreeNode* res = dfs(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1);
        return res;
    }

    TreeNode* dfs(std::vector& preorder, int p_st, int p_en, std::vector& inorder, int i_st, int i_en){
        if(p_st > p_en || i_st > i_en){
            return nullptr;
        }

        // 头结点
        TreeNode *root = new TreeNode(preorder[p_st]);
        // 划分中序
        int pos = -1; // 中序遍历中根节点的位置索引
        for(int i = i_st; i <= i_en; i++){
            if(inorder[i] == root->val){
                pos = i;
                break;
            }
        }
        // 左子树的大小
        int left_size = pos - i_st;
        // 右子树的大小
        int right_size = i_en - pos;

        root->left = dfs(preorder, p_st+1, p_st+left_size, inorder, i_st, pos-1);
        root->right = dfs(preorder, p_st+left_size+1, p_en, inorder, pos+1, i_en);
        return root;
    }
};

int main(int argc, char* argv[]){
    // preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
    std::vector preorder = {3, 9, 20, 15, 7};
    std::vector inorder = {9, 3, 15, 20, 7};
    
    Solution S1;
    TreeNode* res = S1.buildTree(preorder, inorder);

    // 层次遍历打印
    std::queue q;
    q.push(res);
    while(!q.empty()){
        TreeNode* tmp = q.front();
        q.pop();
        std::cout << tmp->val << " ";
        if(tmp->left != nullptr) q.push(tmp->left);
        if(tmp->right != nullptr) q.push(tmp->right);
    }
    std::cout << std::endl;
    return 0;
}