【C++】详解二叉树进阶OJ题（更深入理解递归和非递归在二叉树的各种结构的应用）

前言：

    我们在此前的初阶数据结构讲解中已经讲解了部分二叉树的OJ题，当时我们只学习了C语言，其实还有很多进阶的OJ题用C++来写会比较方便和容易理解，所以本章将在讲解完二叉搜索树后来详解不同类型的二叉树进阶OJ题，校招中涉及也比较多哦！

目录

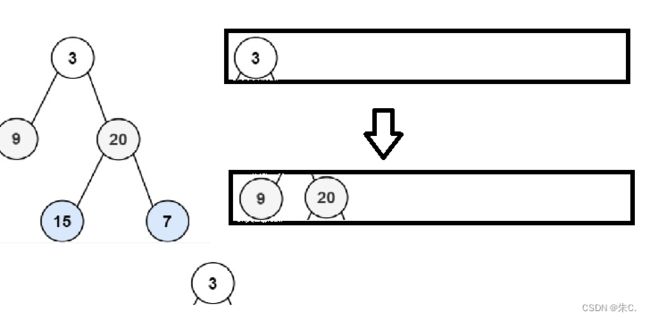
（1）根据二叉树创建字符串

（2）二叉树的层序遍历（一）

（3）二叉树的层序历遍（二）

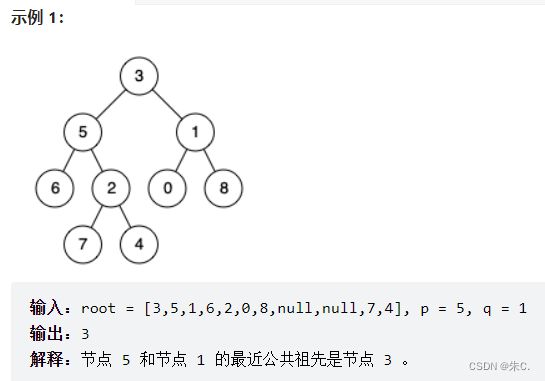
（4）二叉树的最近公共祖先

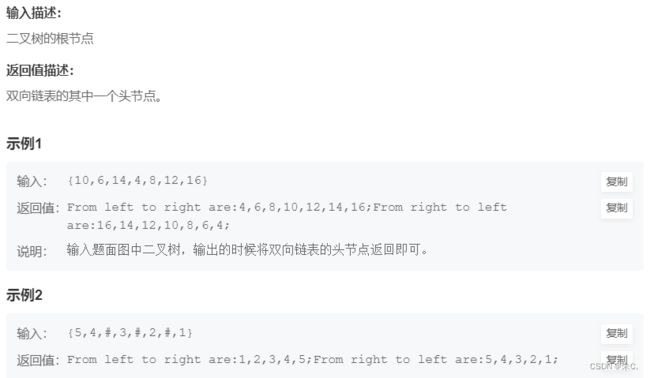
（5）二叉搜索树与双向链表

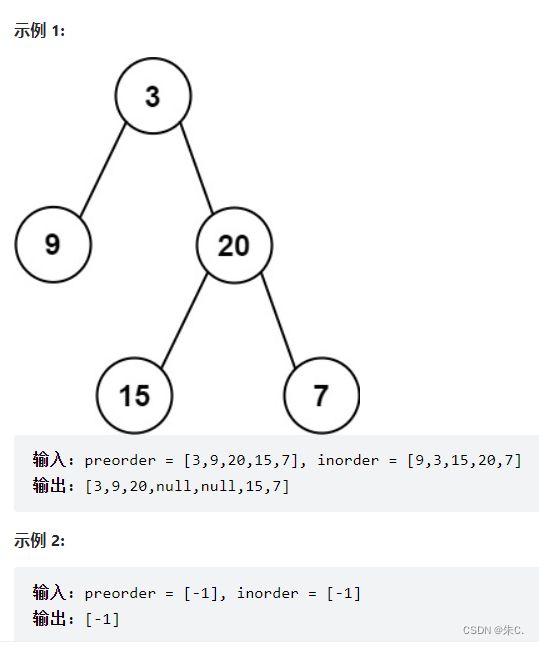
（6）根据一棵树的前序遍历与中序遍历构造二叉树

 （7）根据一棵树的中序遍历与后序遍历构造二叉树

（8）非递归迭代实现二叉树的前序遍历

 （9）非递归迭代实现二叉树的中序遍历

 （10）非递归迭代实现二叉树的后序遍历

---

（1）根据二叉树创建字符串

力扣https://leetcode.cn/problems/construct-string-from-binary-tree/

 

 解析：

这道题目基本就是一个前序排序，但是要额外加上左右括号。

需要特别注意的是，有的空括号要保留，而有的空括号我们则要省略。

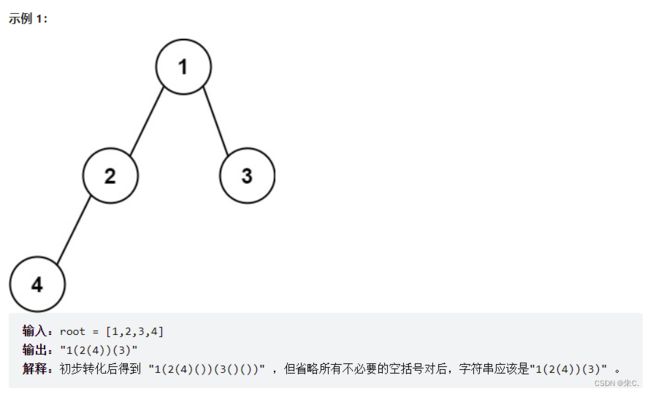
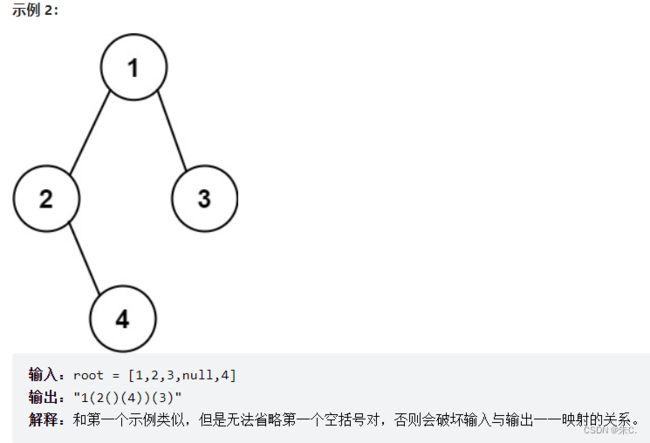
我们观察分析上面的两个样例：

• 当一个结点的左子树为空，但右子树不为空时我们要加空括号来确定；
• 如果同时为空或者右子树为空，则可以省略。

我们采用递归的思想前序历遍，加以条件判断并加上左右括号：

class Solution {
public:
    string tree2str(TreeNode* root) {

     if(root==nullptr)
     return "";

     string str=to_string(root->val);
     if(root->left||root->right)
     { 
         str+='(';
         str+=tree2str(root->left);
         str+=')';
         }
    
     if(root->right)
     {
          str+='(';
          str+=tree2str(root->right);
          str+=')';
     }
    
    return str;
    }
};

（2）二叉树的层序遍历（一）

力扣https://leetcode.cn/problems/binary-tree-level-order-traversal/

 

 解析：

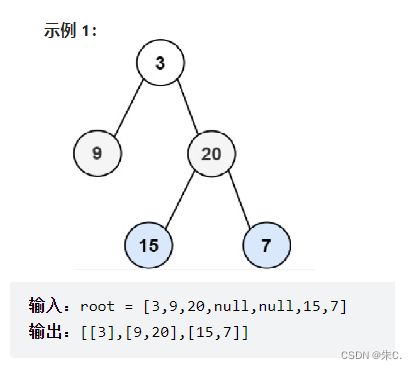
我们仔细观察会发现本题就是层序历遍二叉树并每层的结点存放在一个二维数组里。

难点在于：

• 一是如何层序历遍二叉树；
• 二是每层的结点数目不一样，怎样把握存放在二维数组的同一行中。

我们带着疑问来进一步分析：

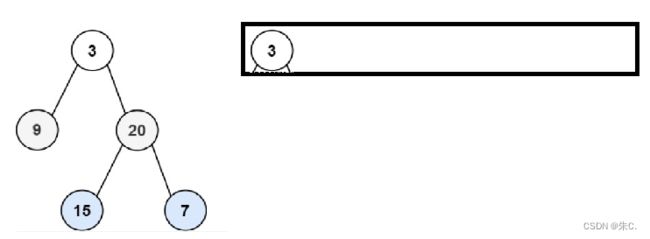
层序历遍二叉树，我们此前其实学过，再带领大家回忆一下：

我们要有一个队列，先存放根节点：

 然后记录队列的头并pop掉，然后带着他的左右孩子入队列：

 我们再重复上面的操作直到队列为空和访问完所有结点为止！

---

二是我们如何让每一层的结点恰好存放在二维数组的每一行中？

我们可以设置一个levelsize变量，根节点进完队列就为1，然后用循环控制pop的次数，此时只有根节点循环一次即可 ，最后入完左右孩子在把队列的长度赋给levelsize，重复这样的操作即可。

class Solution {
public:
    vector> levelOrder(TreeNode* root) {
queue q;
int levelsize=0;
if(root)
{
    q.push(root);
    levelsize=1;
}
vector> vv;
while(!q.empty())
{
vector v;
while(levelsize--)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);

if(front->left)
q.push(front->left);

if(front->right)
q.push(front->right);
}

vv.push_back(v);
levelsize=q.size();
}
return vv;
    }
};

（3）二叉树的层序历遍（二）

力扣https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/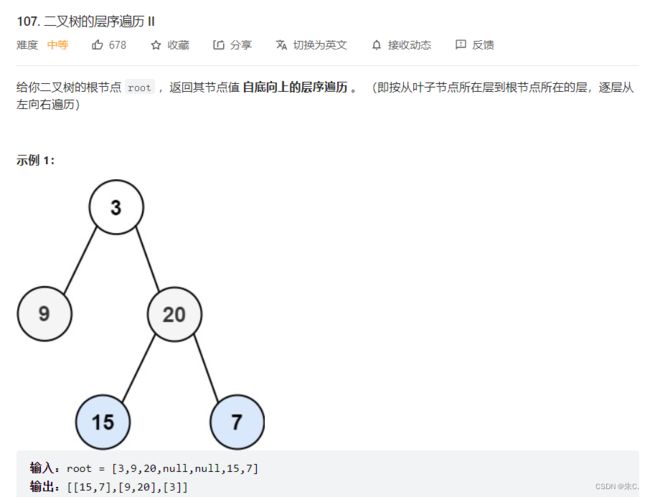

 这道题目就有点像上面那道题目的进阶版本。

乍一看感觉这道题目很恐怖，我们又没学过从底层向上的层序遍历啊，这该怎么办？

这里大家观察一下样例的输出结果和第二道题样例的输出结果：、

 哈哈，想必大家看出端倪了吧，其实就是二维数组中行的逆序，同样的方法，控制好最后的逆序就行了：

class Solution {
public:
    vector> levelOrderBottom(TreeNode* root) {

queue q;
int levelsize=0;
if(root)
{
    q.push(root);
    levelsize=1;
}
vector> vv;
while(!q.empty())
{
vector v;
while(levelsize--)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);

if(front->left)
q.push(front->left);

if(front->right)
q.push(front->right);
}

vv.push_back(v);
levelsize=q.size();
}
reverse(vv.begin(),vv.end());
return vv;
    }
};

（4）二叉树的最近公共祖先

力扣https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

 

解析：

 这道题下面作者会给出两种思路。

思路一：

我们通过观察其实这道题目的公共祖先可以转化为，这两个结点在从上往下的哪个结点的两边。

class Solution {
public:
    bool IsInTree(TreeNode* root, TreeNode* x)
    {
        if(root==nullptr)
        return false;

        
        return root==x
            ||IsInTree(root->left,x)
            ||IsInTree(root->right,x);
        
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr)
        return nullptr;

        if(p==root||q==root)
        return root;

       
            bool PInleft=IsInTree(root->left,p);
            bool PInRight=!PInleft;

            bool QInleft=IsInTree(root->left,q);
            bool QInRight=!QInleft;
            

            if((PInleft&&QInRight)||(PInRight&&QInleft))
            return root;

            else if(PInleft&&QInleft)
            return lowestCommonAncestor(root->left,p, q);

            else
            return lowestCommonAncestor(root->right,p, q);



    }
};

---

思路二：

求出这两个结点到根节点的路径，按照链表那一章讲过的方法，找到两条路径第一个公共结点。

ps：由于空间复杂度的限制以及结点没有指向父结点的指针，我们在实现思路二时候需要用到栈。

class Solution {
public:
bool Getpath(TreeNode* root,TreeNode* x,stack& path)
{
    if(root==nullptr)
    return false;

    path.push(root);
    if(root==x)
    return true;

    if(Getpath(root->left,x,path))
    return true;

    if(Getpath(root->right,x,path))
    return true;

    path.pop();
    return false;
}

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack pPath;
        stack qPath;

        Getpath(root,p,pPath);
        Getpath(root,q,qPath);

        while(pPath.size()!=qPath.size())
        {
            if(pPath.size()>qPath.size())
            pPath.pop();
            else
            qPath.pop();
        }

        while(pPath.top()!=qPath.top())
        {
            pPath.pop();
            qPath.pop();
        }

return pPath.top();
    }
};

（5）二叉搜索树与双向链表

二叉搜索树与双向链表_牛客题霸_牛客网【牛客题霸】收集各企业高频校招笔面试题目，配有官方题解，在线进行百度阿里腾讯网易等互联网名企笔试面试模拟考试练习,和牛人一起讨论经典试题,全面提升你的技术能力https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking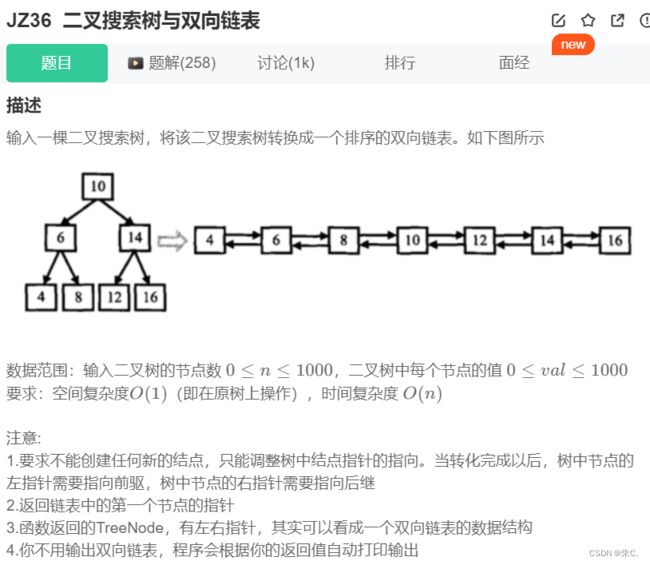

 

 解析：

这道题目有点类似线索二叉树。

这里我们要注意这道题目要求的空间复杂度是O（1），所以我们必须在原树上操作。

我们答题思路就是：

• 中序历遍二叉树，并且结点相互链接上。
• 主要就是如何实现链接，主要用两个变量prev和cur保存历遍前后的地址然后链接、移动...

请看代码：

class Solution {
public:
    void InOrder(TreeNode* cur,TreeNode*& prev)
	{
    if(cur==nullptr)
	return;

	InOrder(cur->left,prev);
	
	cur->left=prev;
    if(prev)
	prev->right=cur;
	prev=cur;//链接过程

    InOrder(cur->right,prev);
	}


    TreeNode* Convert(TreeNode* pRootOfTree) {
        TreeNode* prev=nullptr;
    InOrder(pRootOfTree,prev);

	TreeNode* root=pRootOfTree;
	while(root&&root->left)
	root=root->left;

	return root;
    }
};

（6）根据一棵树的前序遍历与中序遍历构造二叉树

力扣https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/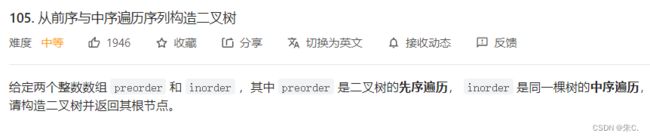

解析：

我们以实例1为例，我们取preorder的第一个，其实也就是根节点，我们再把根节点对应在中序序列中观察：

 我们发现在中序序列中，3的左侧是他的左子树，右侧是他的右子树。

我们再在前序序列中看下一个数：

 9的左右子树都是空，所以在序列中只有9，再继续看下一个：

我么你发现了3右侧这个区间中，20的左侧是左子树，20的右侧是他的右子树，此时我们便大致了解了规律。

class Solution {
public:
TreeNode* _buildTree(vector& preorder, vector& inorder,int& prei,int inbegin,int inend)
{
    if(inbegin>inend)
    return nullptr;

    TreeNode* root=new TreeNode(preorder[prei]);
int rooti=inbegin;
while(rooti<=inend)
{
    if(inorder[rooti]!=preorder[prei])
    {
        rooti++;
    }
    else
    {
        break;
    }}
    ++prei;
    root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);
    root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);
    return root;
}
    TreeNode* buildTree(vector& preorder, vector& inorder) {
int prei=0;
return _buildTree(preorder,inorder,prei,0,inorder.size()-1);
    }
};

 注意区间范围，此外大家可以画递归展开图理解哦！

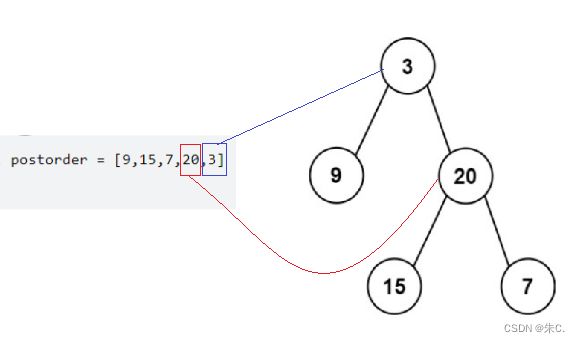
 （7）根据一棵树的中序遍历与后序遍历构造二叉树

力扣https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/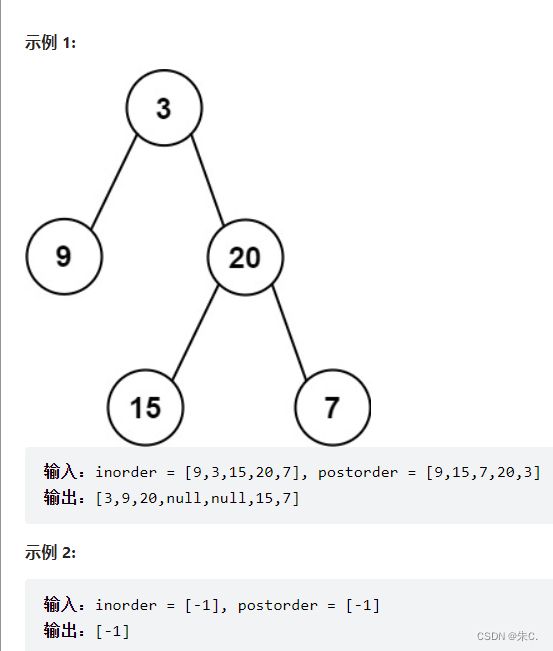

 解析：

这道题和上面一道题类似，我们需要应用好后序和中序的关系，从后面开始历遍。

ps：这里需要注意的是，后序历遍是先历遍右树，再历遍左树：

class Solution {
public:
TreeNode* _buildTree(vector& inorder, vector& postorder,int& i,int inbegin,int inend)
{
if(inbegin>inend)
return nullptr;
int rooti=inbegin;
TreeNode* root=new TreeNode(postorder[i]);
while(rooti<=inend)
 { if(inorder[rooti]!=postorder[i])
    {
        rooti++;
    }
    else
    {
        break;
    }
}

--i;
root->right=_buildTree(inorder,postorder,i,rooti+1,inend);
root->left=_buildTree(inorder,postorder,i,inbegin,rooti-1);

return root;
}

    TreeNode* buildTree(vector& inorder, vector& postorder) 
    {
    int i=postorder.size()-1;
    return _buildTree(inorder,postorder,i,0,inorder.size()-1);
    }
};

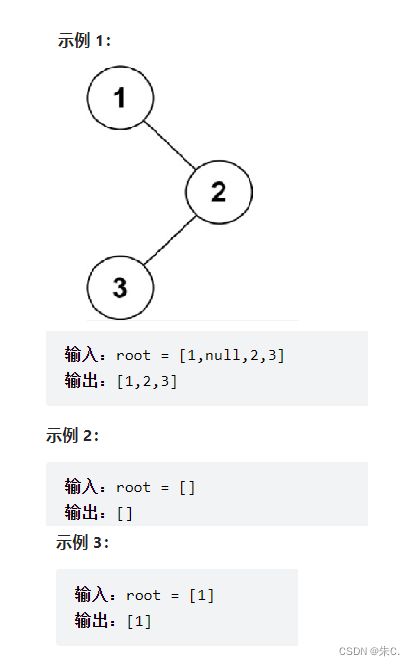
（8）非递归迭代实现二叉树的前序遍历

力扣https://leetcode.cn/problems/binary-tree-preorder-traversal/

 解析：

对于二叉树的遍历，我们用递归实现很简单。但是如何使用非递归实现呢？

我们借用递归的思路，用栈来模拟递归的过程。

我们使用栈来进行迭代，过程如下：

• 初始化栈，并将根节点入栈；
• 当栈不为空时：
• 弹出栈顶元素 node，并将值添加到结果中；
• 如果 node 的右子树非空，将右子树入栈；
• 如果 node 的左子树非空，将左子树入栈；
• 由于栈是“先进后出”的顺序，所以入栈时先将右子树入栈，这样使得前序遍历结果为 “根->左->右”的顺序。

 

class Solution {
public:
    vector preorderTraversal(TreeNode* root) {

vector v;
stack st;
TreeNode* cur=root;
while(cur||!st.empty())
{
    while(cur)
    {
        st.push(cur);
        v.push_back(cur->val);
        cur=cur->left;
    }
    TreeNode* top=st.top();
    st.pop();
    cur=top->right;
}

return v;
    }
};

 （9）非递归迭代实现二叉树的中序遍历

力扣https://leetcode.cn/problems/binary-tree-inorder-traversal/

 解析：

中序遍历可以参考前序遍历的过程，思路是一样的。

class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
stack st;
vector v;
TreeNode* cur=root;

while(cur||!st.empty())
{
    while(cur)
    { 
        st.push(cur);
        cur=cur->left;
    }
     TreeNode* top=st.top();
     st.pop();
     v.push_back(top->val);
     cur=top->right;

}
return v;
    }
};

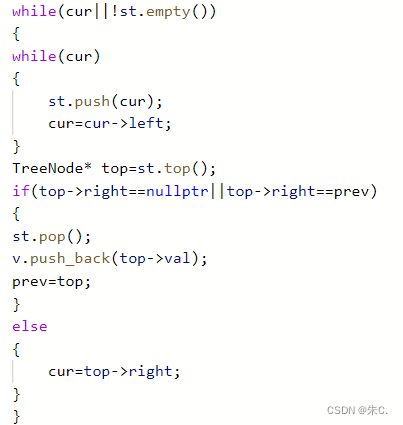
 （10）非递归迭代实现二叉树的后序遍历

力扣https://leetcode.cn/problems/binary-tree-postorder-traversal/

 

 相对于前序，中序来说，后序的实现过程更麻烦一点。

这里我们呢还是像前面一样通过循环找到最左的元素（注意保存在栈中），但是要注意：迭代写法，利用pre记录上一个访问过的结点，与当前结点比较，如果是当前结点的子节点，说明其左右结点均已访问，将当前结点出栈，更新pre记录的对象。

循环过程如下： 

完整代码：
 

class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
vector v;
stack st;
TreeNode* cur=root;
TreeNode* prev=nullptr;
while(cur||!st.empty())
{
while(cur)
{
    st.push(cur);
    cur=cur->left;
}
TreeNode* top=st.top();
if(top->right==nullptr||top->right==prev)
{
st.pop();
v.push_back(top->val);
prev=top;
}
else
{
    cur=top->right;
}
}
return v;
    }
};

ps：取巧的方法。该写法的访问顺序并不是后序遍历，而是利用先序遍历“根左右”的遍历顺序，将先序遍历顺序更改为“根右左”，反转结果List，得到结果顺序为“左右根”。（不建议用）