保留网络[02/3]:大型语言模型转换器的继任者”
一、说明
二、关于RetNet的开源处
保留网络(RetNet)具有与相同大小的转换器相当的性能,可以并行训练,但支持递归模式,允许每个令牌的O(1)推理复杂性。
非官方但完整的实现可以在下面的我的回购中找到:
GitHub - syncdoth/RetNet:RetNet 的完整实现(Retentive Networks...
RetNet(保留网络,https://arxiv.org/pdf/2307.08621.pdf)的完整实现,包括并行...
github.com
三、生成序列模型的“不可能三角”
对于序列模型,尤其是生成模型,我们有上述三个特点:快速推理、并行训练和强大的性能。(在我看来,还有一个维度:序列长度外推。RetNet 可能支持这一点,但没有明确的实验。
RNN 具有快速推理但训练缓慢,线性变压器的性能较弱,变压器每个令牌推理具有 O(n)。RetNet满足所有三个条件: 并行训练、O(1) 推理和节拍变压器。
四、快速历史记录
有多种方法可以减轻生成变压器的昂贵推理。著名的作品包括Linear Transformers,Attention-Free Transformers(AFT;来自Apple)和RWKV(来自BlinkDL,基于AFT)。
这些值得单独发布,所以我不会详细介绍:但在我看来,它们在数学上都非常优雅,尤其是 RNN 如何并行化的推导。而我发现 RetNet 更有趣,因为它也有块表示和一些漂亮的技巧,如 xpos。
五、那么这是如何工作的呢?
RetNet 是在同一 Transformer 架构中将“注意力”替换为“保留”的即插即用替代。
我将以自上而下的方式介绍它们。
5.1. 每个 RetNet 块
每个 RetNet 块的公式。
在最高级别,RetNet 由几个相同的块堆栈组成,每个堆栈都包含 MultiScaleRetention (MSR) 和 FeedForwardNetwork (FFN)。它们还具有层规范和跳过连接,与变形金刚相同。FFN也几乎与变形金刚相同,后者是2层MLP,隐藏的暗光尺寸= 2倍嵌入尺寸,并具有gelu激活功能。
如果我们用MultiHeadAttention代替MSR,这只是Transformer。因此,所有差异都可以在MSR中找到。
5.2. 门控多尺度保留
多尺度类似于多头。在上面的等式中,γ是一些用于保留的超参数,这是为每个头部单独定义的。在群体规范之前,这是普通的多头关注,但保留。
门控MSR在输出端增加了组范数、旋门和输出投影,可视为辅助设计选择。(组规范允许缩放点积,但目前并不那么重要。 最重要的区别(保留模块)尚未到来。
5.3. 保留
最后,让我们看看什么是保留。保留有 3 种范式:并行、循环和块递归。让我们一一看一下。
并行保留
保留的并行表示
专注于最后一行。忽略 D,再次,这是没有 softmax 的点积关注。所以重要的细节又在D和Theta中。
- Theta(和bar(Theta),复共轭)是“xpos编码”的复杂表示 - 它建立在旋转嵌入的基础上,以便模型可以更好地推断序列长度。在非复杂空间中存在相同的表示,这正是基于 RoPE 构建的 xpos。
请参阅 xpos 白皮书。我还发现这篇讲义有助于理解这一点。
- D是因果掩蔽+衰变矩阵。
如果绘制 D,则 D 如下所示:
gamma = 0.9
exponent = [[0, 0, 0, 0],
[1, 0, 0, 0],
[2, 1, 0, 0],
[3, 2, 1, 0]]
D = tril(gamma**exponent)
# [[1., 0., 0., 0.],
# [0.9000, 1., 0., 0.],
# [0.8100, 0.9000, 1., 0.],
# [0.7290, 0.8100, 0.9000, 1.]])- 上三角形为 0 →因果掩蔽。
- 指数 = 前一个令牌表示被衰减的次数。当我们看到反复出现的表示时,这一点将变得更加清晰。
经常性保留
经常性保留
Sn类似于变压器中的KV缓存。RetNet 不是按顺序连接所有这些矩阵,而是将它们聚合成一个矩阵,循环在第一行。然后,此值乘以当前步骤的查询。
这与并行保留完全相同。
非正式证明草图:
设 S_0 = 0。 如果我们解决了S_n的复发,
回想一下平行表示中 D 的指数矩阵的最后一行,即 [3, 2, 1, 0]。请注意,n=4。当我们计算第 4 个代币与第 1 个代币的保留期时,我们将其衰减 3 倍,相当于上式中的 n — i = 3! 由于其余部分相同,因此并行表示和循环表示彼此相同。
分块保留
这看起来很复杂,但它实际上是每个块的并行计算 + 块的循环连接。 唯一重要的是应用的衰减次数。
5.4 论文中的错误
实际上,论文对 Ri 的分块表示(上面的等式)是错误的!事实上,它应该是
其中 X 运算符是叉积,D_B 是 D 矩阵的最后一行。直观地说,这是从平行表示和循环表示的衰减乘法得出的。
5.5 示意图
就是这样!以上是两种表示的摘要图。
六、为什么衰变?
所以基本上,最重要的细节是它使用了一种叫做衰减的东西,并且应用正确的衰减次数允许并行化。但我们必须了解这种衰败背后的动机是什么。推导(在高级别)非常简单。
- 我们将循环状态(s_n)定义为kv_cache。然后,递归关系在上图的第一行。
- 然后,我们将时间 n 的输出定义为 Q_n * s_n。上面的第二行写了这个并解决了重复周期以推出完整的依赖项。请注意,矩阵被多次应用。
3.现在,我们将A矩阵对角化为以下内容。
4. 然后,可以将 Λ 符号吸收到其他可学习的参数中(Q_n = X * W_k,因此 Λ 可以吸收到 W_k!因此,我们只剩下中间部分。
中间部分正是我们之前观察到的γ(衰变)和θ。
直观地说,它们作为一种“封闭式位置编码”工作,它也具有递归形式,因此可以提前计算时间n的编码,从而实现并行化。
七、实证发现
- RetNet击败了Transformer,因为它变得更大了。(评论家:不确定这种趋势是否会持续下去)
- RetNet在性能上击败了其他线性时间转换器。
- RetNet很快。(批评者:根据架构,这是显而易见的。显示 3 个数字来强调这一点毫无意义。TBH,甚至不需要运行实验来绘制这些情节......
八、评论家
- 论文中缺少一些细节,在官方代码出来之前不会明确。
- RWKV也支持训练并行化,但在论文中被歪曲为不可能。
- 有点吹嘘 RetNet 很快,有 3 个数字说同样的事情。:-)
- 很好奇这种趋势是否会扩展到更大的模型。
- 不确定他们是否会释放预先训练的体重。
- 不确定他们是否会击败像LLaMA这样的模型。
九、优点
- 快!(我批评他们吹牛,但确实很快,这很好)
- 性能相当。如果这种趋势继续下去,并且大型型号的性能没有下降,这可能会成为LLM的事实,因为它们便宜得多。
崔世贤
对于那些感兴趣的人,请看一下我对RetNet的实现:
GitHub - syncdoth/RetNet: Huggingface compatible implementation of RetNet (Retentive Networks, https://arxiv.org/pdf/2307.08621.pdf) including parallel, recurrent, and chunkwise forward.
![保留网络[02/3]:大型语言模型转换器的继任者”_第1张图片](http://img.e-com-net.com/image/info8/bb6853d023cf4df4baae8ca78193b042.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第2张图片](http://img.e-com-net.com/image/info8/cdaef0cc85f04bbd9820ea524e9f8cab.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第3张图片](http://img.e-com-net.com/image/info8/d99a72035f424e28bf2d5956a162c295.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第4张图片](http://img.e-com-net.com/image/info8/75af575251584c83ba60a909769c86d5.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第5张图片](http://img.e-com-net.com/image/info8/f30402c2e15f4a61b639b369db2b266f.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第6张图片](http://img.e-com-net.com/image/info8/8d71efe76b7e4a8d8cb2e1d70d8c004a.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第7张图片](http://img.e-com-net.com/image/info8/a5349e58f6ed47a8affc6f1809b07d25.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第8张图片](http://img.e-com-net.com/image/info8/c617ee58186c4894a08bcfaa991dbe65.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第9张图片](http://img.e-com-net.com/image/info8/aa055b3f56a446f584bf4c68f3ed3fc1.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第10张图片](http://img.e-com-net.com/image/info8/431345390b804157bba5b3defe844144.jpg)
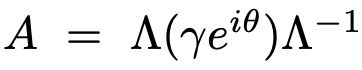
![保留网络[02/3]:大型语言模型转换器的继任者”_第11张图片](http://img.e-com-net.com/image/info8/2c252f792e7348a199aeec0de1a014d8.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第12张图片](http://img.e-com-net.com/image/info8/8db23c3b2b1a4948a6f4e699b94d22c5.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第13张图片](http://img.e-com-net.com/image/info8/c5f1ca4b51234d9db25f7e12f62910ab.jpg)
![保留网络[02/3]:大型语言模型转换器的继任者”_第14张图片](http://img.e-com-net.com/image/info8/6f5abef9f02c488f9d1c886b0223c271.jpg)