2023年第六届河北省研究生数学建模竞赛题目B题Python求解代码
2023年第六届河北省研究生数学建模竞赛题目B题
本文文档与代码视频讲解与下载:【2023河北省研究生数学建模竞赛B题数据集和代码-哔哩哔哩】 https://b23.tv/weulGAO
光伏电池的异常检测与发电产能预测在碳达峰-碳中和的战略背景下,我国的光伏发电技术发展迅猛。我国风电、太阳能发电总装机容量预计在 2030年目标达到 12亿千瓦以上。光伏发电是利用半导体界面的光生伏特效应而将光能直接转变为电能的一种技术。这种技术的关键元件是 光伏 电池, 其 经过串联后进行封装保护可形成大面积的 光伏 电池组件,再配合功率控制器等部件就形成了光伏发电装置。
光伏发电受到光伏组件质量、 气象因素、太阳辐照度和使用情况等因素影响,从而出现发电量的波动。光伏组件主要是由许多个光伏晶体硅片组成的半导体硅太阳能电池拼接而成。在组件的制造、运输以及使用过程中会产生各种缺陷, 例如线状裂纹、星形裂纹、断栅、黑芯、粗线等 (同一光伏电池可具有多项 缺陷 。 这些缺陷会不同程度地降低组件的光电转换效率和可靠性。 例 如图 1 的光伏电池电致发光( EL)图像标记为无缺陷,表面能明显看出电池整体完好;图 2 的光伏电池 EL图像 包含线状 裂纹 类型缺陷 。
图 1 无缺陷的光伏电池样品
图 2 表面缺陷的光伏电池样品
同时气象因素也是影响光伏发电的一个重要因素,包括风速、温度、湿度、太同时气象因素也是影响光伏发电的一个重要因素,包括风速、温度、湿度、太阳辐照度、突发的极端天气情况等等,可能导致光伏发电效率下降,从而影响整个阳辐照度、突发的极端天气情况等等,可能导致光伏发电效率下降,从而影响整个能源系统的稳定性。阴天、大气污染、太阳高度等也会影响照射在光伏板上的太阳能源系统的稳定性。阴天、大气污染、太阳高度等也会影响照射在光伏板上的太阳光的强度。此外,太阳辐射强度和方向的变化也可能导致光伏发电量的波动,从而光的强度。此外,太阳辐射强度和方向的变化也可能导致光伏发电量的波动,从而影响整个能源系统的稳定性。影响整个能源系统的稳定性。
现有一批某地区光伏发电的相关数据,工作者依据这些数据已将其分为图像现有一批某地区光伏发电的相关数据,工作者依据这些数据已将其分为图像和数据两种类型。附件和数据两种类型。附件1给出了一些光伏给出了一些光伏EL电池图像,电池图像, 附件附件 2给出了给出了2020年年和和2021年的气象数据,附件年的气象数据,附件3给出了给出了2020年和年和2021年的发电产能数据,附件年的发电产能数据,附件4给出了历史数据。给出了历史数据。
请你们团队依据附件中的相关数据进行分析建模,解决以下问题:请你们团队依据附件中的相关数据进行分析建模,解决以下问题:
问题1数据集
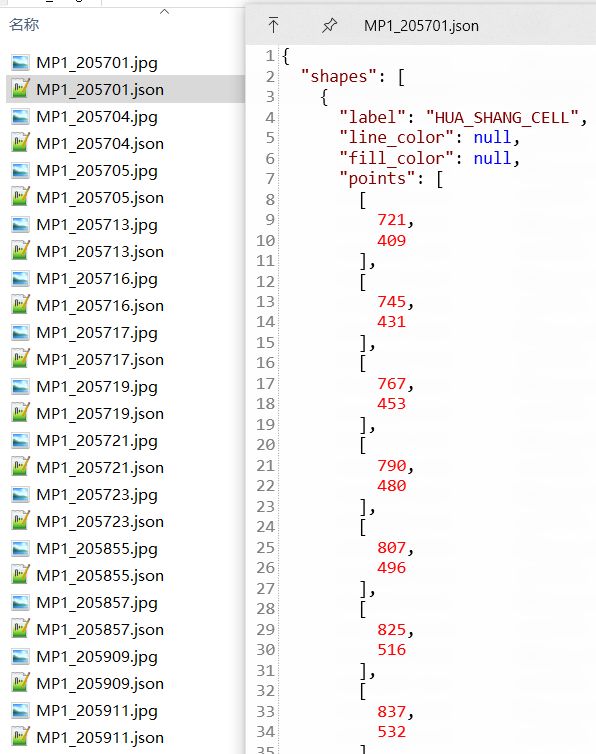
问题 1 自行查阅光伏EL电池组件图像资料,并构建自己的光伏电池缺陷数,对构建的数据集进行建模,对附件1的图片进行缺陷检测,将检测结果填入下表,并对检测结果的合理性进行分析。
目前已找到的数据集如下,分为标注和图片,以及测试图片,共400+MB,含标注,
数据集:太阳能电池的 PV EL 异常检测数据集,其中包含 36,543 个具有各种内部缺陷和异质背景的近红外图像。该数据集包含 1 类无异常图像和 12 个不同类别的异常图像,包括裂纹(线和星)、手指中断、黑芯、错位、粗线、划痕、碎片、角和材料缺陷等。此外,还为 12 种缺陷提供了 40358 个真实边界框
数据集处理:可使用目标检测方法如yolo、SSD等算法,对训练的mAP进行评估等
问题2
2023年河北省研究生数学建模B题问题 2:请根据附件 2气象数据( 15min时间间隔),对数据进行预处理,建立气象模型,对2021年 11月 12-18日的风速、风向、温度等数据进行预测,并完成下表。
当涉及时间序列预测时,ARIMA(自回归移动平均模型)和SARIMA(季节性自回归移动平均模型)是常用的统计模型。它们都用于拟合时间序列数据,捕捉其中的趋势、季节性和周期性等特征,并进行未来值的预测。同时,ACF(自相关函数)和PACF(偏自相关函数)是时间序列数据的重要工具,用于确定ARIMA和SARIMA模型的阶数。
1. ARIMA(自回归移动平均模型):- ARIMA是一个常用的时间序列预测模型,它结合了自回归(AR)和移动平均(MA)的特性,用于拟合非平稳时间序列数据。
-
AR(自回归)部分使用时间序列数据自身的滞后值来预测未来值,表示为AR(p);MA(移动平均)部分使用滞后误差项来预测未来值,表示为MA(q)。
-
差分(d)用于将非平稳数据转换为平稳数据,使其满足ARIMA模型的前提条件。
-
ARIMA(p, d, q)是AR、I(差分)和MA的组合,其中p、d和q是分别对应AR、I和MA的阶数。
2. SARIMA(季节性自回归移动平均模型):- SARIMA是ARIMA模型的扩展版本,专门用于处理具有季节性的时间序列数据。
-
除了ARIMA模型的p、d和q参数外,SARIMA还有季节性的AR、I和MA参数,表示为AR(P)、I(D)和MA(Q)。
-
季节性周期(s)用于指定数据中季节性的间隔,例如一年365天或一周7天。
-
SARIMA(p, d, q) × (P, D, Q, s)是SARIMA模型的表示方式,其中p、d、q分别对应AR、I和MA的阶数,P、D、Q分别对应季节性AR、I和MA的阶数,s是季节性周期。
3. ACF(自相关函数):- ACF用于衡量时间序列数据与其自身滞后值之间的线性相关性。
-
绘制ACF图可以帮助确定时间序列数据是否具有自回归(AR)模型的特征,即数据与其滞后值之间是否存在相关性。
-
如果ACF在滞后值为0之外的阶数上呈现出显著的相关性,则可能需要AR模型。
4. PACF(偏自相关函数):- PACF用于衡量时间序列数据与其自身滞后值之间的直接线性关系,消除了中间滞后值的影响。
-
绘制PACF图可以帮助确定时间序列数据是否具有移动平均(MA)模型的特征,即数据与其滞后值之间是否存在直接的线性关系。
-
如果PACF在滞后值为0之外的阶数上呈现出显著的相关性,则可能需要MA模型。
首先加载数据:
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.stattools import adfuller
# 1. 数据预处理
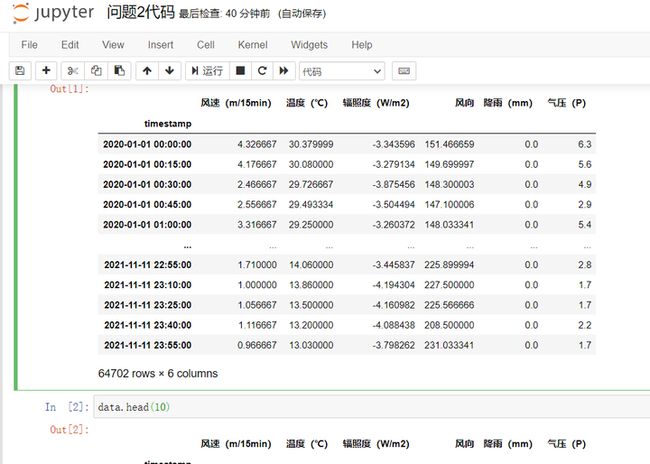
data = pd.read_excel("附件2.xlsx")
data['timestamp'] = pd.to_datetime(data['timestamp'])
data.set_index('timestamp', inplace=True)然后使用使用线性插值填充缺失值
数据可视化:
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一(替换sans-serif字体)
plt.rcParams['axes.unicode_minus'] = False # 步骤二(解决坐标轴负数的负号显示问题)
# 2. 数据可视化
plt.figure(figsize=(12, 6), dpi=300)
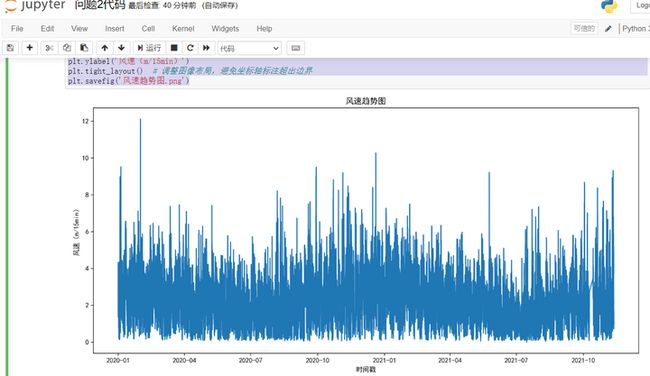
plt.plot(data['风速(m/15min)'])
plt.title('风速趋势图')
plt.xlabel('时间戳')
plt.ylabel('风速(m/15min)')
plt.tight_layout() # 调整图像布局,避免坐标轴标注超出边界
plt.savefig('风速趋势图.png')
然后建立风速的气象模型,进行ACF和PACF检验:
# 3. 建立气象模型 - 风速
wind_speed_data = data['风速(m/15min)']
# Stationarity Check
result = adfuller(wind_speed_data)
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
print('Critical Values:')
for key, value in result[4].items():
print(f' {key}: {value}')然后进行时间序列训练和预测:
# ARIMA 模型拟合 -风向
model_wind_direction = ARIMA(wind_direction_data, order=(p, d, q))
model_fit_wind_direction = model_wind_direction.fit()
# 残差分析 - 可视化并检查残差是否存在模式或显著的偏差。
residuals = model_fit_wind_direction.resid
plt.figure(figsize=(10, 6))
plt.plot(residuals)
plt.title('ARIMA 模型残差(风向)')
plt.xlabel('时间戳')
plt.ylabel('残差')
plt.tight_layout() # 调整图像布局,避免坐标轴标注超出边界
plt.savefig('ARIMA模型残差(风向).png')
# ARIMA模型预测考虑到季节性因素,也可以使用季节性时间序列预测SARIMA来预测:(代码略,下载地址见文章开头)
问题 3 结合问题2所得到的气象数据进行建模,对数据进行预处理,建立气象与发电产能的数学模型,并对2021年年11月月18日的光伏发电产能进行预测,并完成下表
建立气象与发电产能的数学模型,这是个回归问题,可以先使用主成分分析提取主成分,然后使用多种回归方法,如决策树回归、支持向量机回归、XGBoost回归等等