数据结构 | 排序算法——归并排序
Hello大家好,上次我们讲到了冒泡排序和快速排序,本文我们来讲一下排序算法中的归并排序,它是属于外排序的一种
万事万物最终都将归一
- 归并排序的思维
- 递归实现
-
- 先行展现代码
- 代码细究与DeBug调试
- 动画展示
- 非递归实现【校招要求】
-
- 思路分析
- 代码详解
- 特殊情况考虑【边界的修正】
- 整体代码展示
- 总结与提炼
归并排序的思维
首先我们来说一下什么是归并排序,对于归并排序,就是将已有的子序列合并,得到完全有序的序列。即先要将子序列有序,再使子序列段间有序,这样最终这个整体才能有序
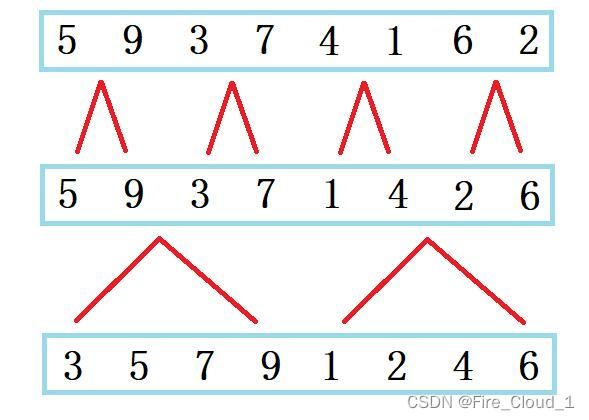
- 我们通过一张图先来了解一下

- 从上述图,大家应该可以对归并排序有一个大体的思路,我们再通过分步算法图来详解一下
- 首先看到,若是有一组数字,我们怎么将其变为有序呢,之前我们有说到,若是一个序列的左边有序,并且右边有序,那么这个序列便会有序
- 所以我们我们先将其分为两部分,然后再将其中的一部分再分为两部分,直到有一个子区间只有一个数为止,那么这个时候再进行一个归并,归并到最原始的左右两区间,下图便是已经归并完成的结果
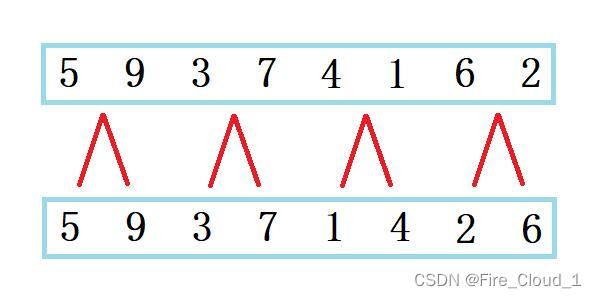
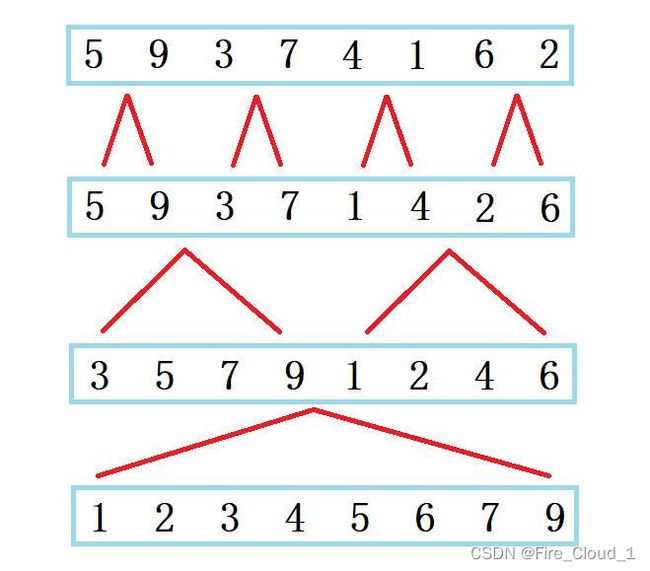
- 然后这个时候我们再取两个指针,分别指向两个区间的首位置
- 接着进行一个比较,选出两个区间中较小的那个数字,放入我们要存放的新数组中,然后指向新数组的指针后移一位,准备存放第二个数值
- 然后将刚才小的那个数所在的区间的指针后移一位,继续与另一区间中指针所指的数进行比较,将较小的数放入新数组中,然后新数组指针后移一位
- 然后大家看这个时候,第一个区间已经遍历完了,但是指针所指的7还是小于右区间中的8,所以其只能后移,此时可以看到,左区间的指针已经超过了其右边界,所以此时我们应该停止这层循环
- 那这个时候应该怎么办呢?新数组中还有两个数没有填入,这个时候不用急,只需要将还没有遍历完的那一个数组中剩余的数字一一放入新数组中即可
- 然后此时当剩余那个区间的指针超过右边界时,便跳出循环,获取到了我们需要的那个新数组
- 看到这里,相信你对归并排序已经有了一定的了解接下去我们进入下一个模块,去看看归并排序的递归形式是怎么实现的
递归实现
先行展现代码
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
{ //若是左右两值不构成区间,则直接返回
return;
}
int mid = (left + right) >> 1; //去中间值——分为两个区间
//[left, mid][mid + 1, right] —— 左右分别递归
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
//此时两侧已然后续,需使用二路归并将他们放到一个临时数组里
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
//二路归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
/*
*此时跳出上面的循环后一定有一个区间已经结束
*但是还有一个区间没结束
*无需比较,直接放入另一数组即可
*/
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//最后将临时数组拷回去
for (int i = left; i <= right; ++i)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int));
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
代码细究与DeBug调试
第一模块已经实现了其原理的算法图,这里便不做详解,我们来跟着DeBug调试来测试一下代码
- 这里的代码逻辑一共是有两层,第一层是主体的归并排序,通过开辟出一个新的数组,用来【暂时存放】我们排序后的内容
- 然后我们将内部的归并单独划分成了一个子函数,通过传入原数组、以及左右边界值已经临时存放的新数组,去实行一个内部的逻辑
_MergeSort(a, 0, n - 1, tmp);
- 然后我们按F5进入这个函数,首先看到最开头的两句,若是进入这个子函数时左右边界不构成一个区间,则直接返回
if (left >= right)
{ //若是左右两值不构成区间,则直接返回
return;
}
- 然后和快排一样,我们去求解它的中间值用于后续的递归使用
int mid = (left + right) >> 1; //去中间值——分为两个区间
- 然后看到这两句代码便是递归左右区间的递归函数,其中左区间的右边界就是当前的mid,右区间的左边界便是mid + 1,
//[left, mid][mid + 1, right] —— 左右分别递归
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
- 可以看到,通过上面的两次递归, 左右区间已然有序,具体内部细节我们不做展开
重点来讲一下如何进行二路归并的部分⭐
- 在这一段代码中,我们需要记录下左右两个子区间的左右边界值,方便后面更新的时候做判断,然后index我们在第一模块也讲到过,就是指向新数组的遍历指针
//此时两侧已然后续,需使用二路归并将他们放到一个临时数组里
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
- 然后最重要的还是这段主题代码
- 我们来看一个这个循环的条件,上面说到过,只要有一个区间已经遍历完了,那么就需要跳出这个循环,所以继续循环的逻辑应该是【当两个区间都没遍历完的时候,便一直循环】
//二路归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
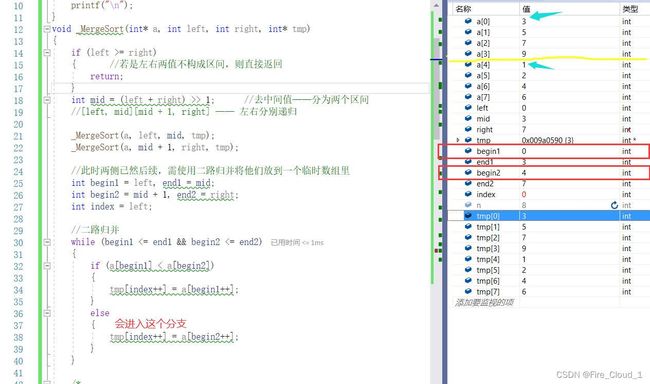
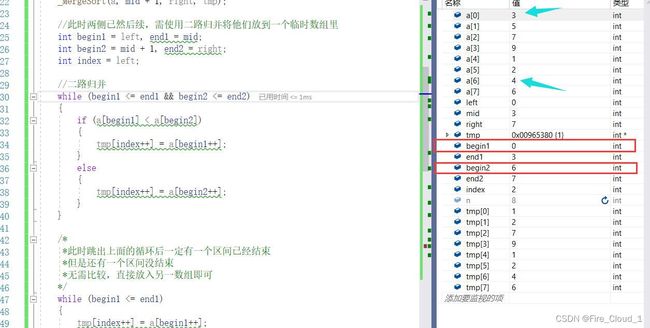
- 然后我们看到,begin1所指位置的值是要大于begin2所指位置的值
- 所以大家仔细看这个 tmp[0],便会更新为begin2所在位置的值,以及这个index和begin2都会向后移动一位
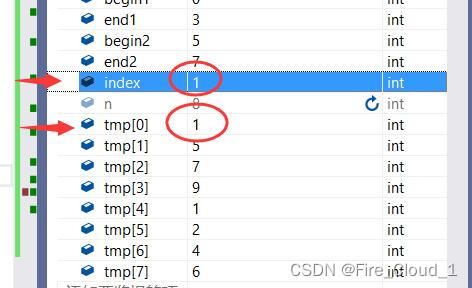
- 然后经过一次的比较,begin2的值便向后移动了一位,我们根据两个begin位置上的值可以看出来,2还是小于3,所以依旧会进入第二个分支
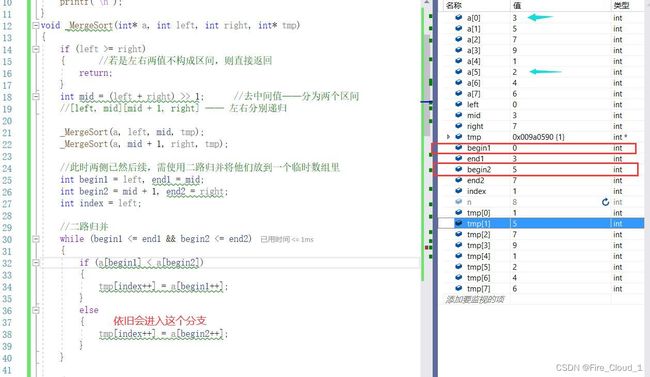
- 这个时候仔细看,tmp[1]上的值会被更新成2,然后index与begin2继续后移一位
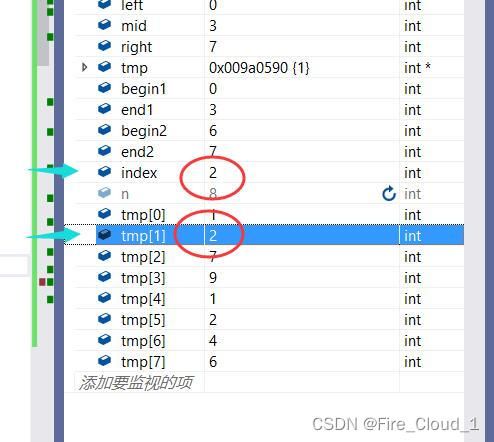
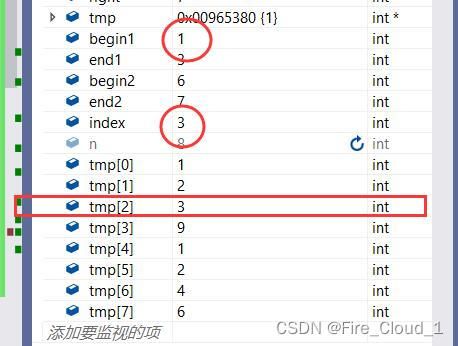
- 然后对比此刻,begin1上的值终于比begin2来的小了,此时便会进入第一个分支,然后tmp[2]位置上的值就会被更新成为3,然后index与begin1指针便会后移一位
- 从DeBug中可以很清晰地看出来
- 然后我们直接快进到这里,因为此时的begin2已经是超过了end2,所以说会跳出上面那个循环,来执行这个循环
/*
*此时跳出上面的循环后一定有一个区间已经结束
*但是还有一个区间没结束
*无需比较,直接放入另一数组即可
*/
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
- 这个时候我们可以看到,新数组中只剩两个数没有填入,此时只需要遍历上面的第一个循环,将7 和 9放入新数组中即可
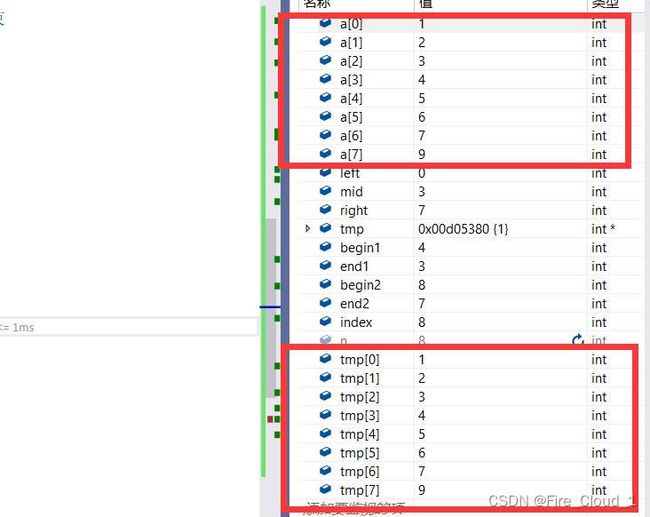
- 最后的话通过下面这段代码,将暂时存放在新数组中的数全部重新拷贝回去即可
//最后将临时数组拷回去
for (int i = left; i <= right; ++i)
{
a[i] = tmp[i];
}
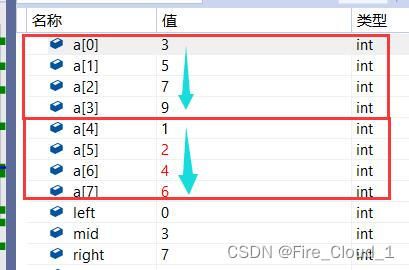
- 最后可以看到,a数组与tmp数组中的值是对应相当的
- 以上就是用递归去实现归并排序的整体代码和思路,大家应该看懂了吧,如果还没有看懂的画,再来通过动画来回顾一遍,然后自己再去实现一下这个代码就行
动画展示
非递归实现【校招要求】
了解了归并排序的递归实现,接下来我们来说一说它的非递归实现,这个的话校招可能会考到,但是平时的期末考试和考研是不会涉及到,大家需要的话继续往下看就行
思路分析
我们首先来分析一下非递归实现归并排序是怎样一个思路
- 首先我们回忆一下,在快速排序中,我们讲到的非递归时是如何实现的,没错,就是利用【堆栈】去实现的,但是在归并中,我们并不使用堆栈去解决这个问题,而是使用【循环】的方式去解决
- 在其他地方可以也会让你用非递归的形式去实现一个递归的算法,大家只要记住,第一时间去想循环,若是循环解决不了,再使用【堆栈】或是【队列】去解决即可
我们来看一下这个整体的思路
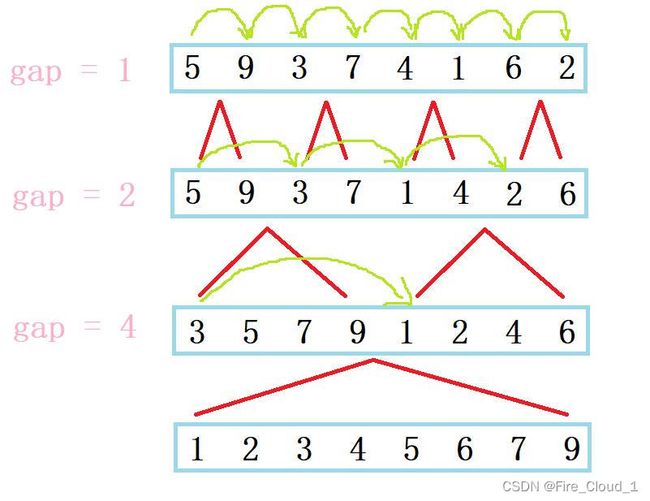
- 对于递归来说,类似于二叉树的后续遍历,先让其左区间有序,然后右区间有序,最后整体有序
- 但是对于非递归来说,我们采取这个思路,首先将这一组数据一个和一个进行归并,然后对他们进行一个比较,使其变为有序
- 然后便是将余下的数字两两分为一组,继续进行一个归并
- 然后就是4个4个一组,那也就是将整体进行一个排序
- 可以看到,这个每次分组的数据量都是以2的倍数在递增的,因为我们可以设置一个gap值,在外层写一个循环,若是gap < n,便一直循环执行,因为gap > n后边越界了
- 这个gap是不是很熟悉,没错就是我们在希尔排序这一文中有讲到过这个gap值,但是在希尔中这个gap值是递减的,而在归并中我们这个gap值需要递增,直到大于n为止,所以
代码详解
讲完了整体的整个思路,接下来来看看代码是怎么写的
- 其实内部的交换逻辑还是和递归一样的,就是不需要这个层层递归下去,也就不需要去取那个中间值了
void MergeSort_NoRecursive(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += gap * 2)
{
//[i, i + gap - 1][i + gap, i + 2 * gap - 1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = i;
//二路归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
/*
*此时跳出上面的循环后一定有一个区间已经结束
*但是还有一个区间没结束
*无需比较,直接放入另一数组即可
*/
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
//最后是将每组归并完后的数据全部拷贝回去,供下一次归并使用
for (int j = 0; j < n; ++j)
{
a[j] = tmp[j];
}
gap *= 2; //每次归并完gap * 2
}
free(tmp);
}
- 但是对于边界值还是需要变化的,因为随着这个gap值不断增加,子区间的大小也会不断的产生一个变动
- 第一点就是这个for循环的增值逻辑,从下面这样图可以看到,每次的这个gap
for (int i = 0; i < n; i += gap * 2)
- 所以对于这两行的代码逻辑,还是要重点理解,去搞清楚每一次这个边界值与gap之间的关系
//[i, i + gap - 1][i + gap, i + 2 * gap - 1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
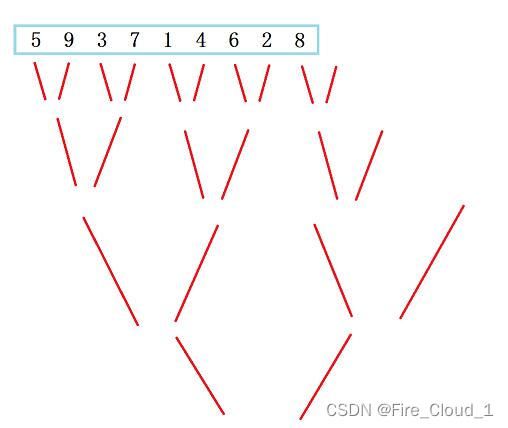
- 我们通过图示来更加清晰地观察一下。通过gap值的这个边界计算,我们得出了每一次的区间值
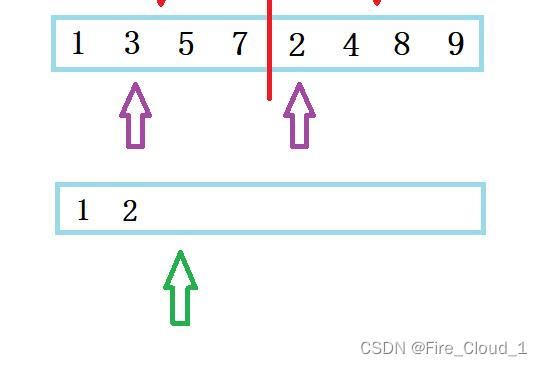
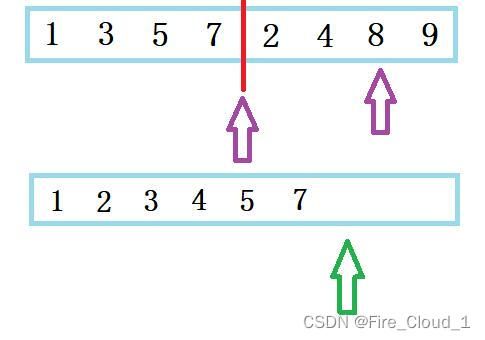
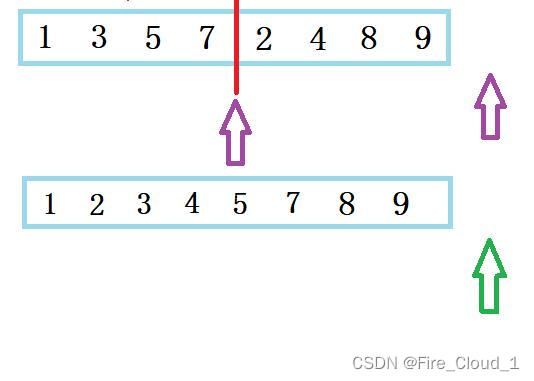
- 可以看出:当gap = 1时,便是[0,0],[1,1],那也就是自己和自己做比较,然后两个值进行一个归并就是排序后的子序列
- 当gap = 2时,便是[0,1],[2,3],那也就是两两做比较,然后四个数进行一个归并就是排序后的子序列
- 最后可以看到,这个数据拷贝是放在for循环遍历之后的,这是为什么呢?
- 因为并不是归并完一组就将这个临时数组中存的值拷回去,而是要在所有组都归并完之后一起拷贝回去,这样才是当下这一个gap值所呈现的完整数组
//最后是将每组归并完后的数据全部拷贝回去,供下一次归并使用
for (int j = 0; j < n; ++j)
{
a[j] = tmp[j];
}
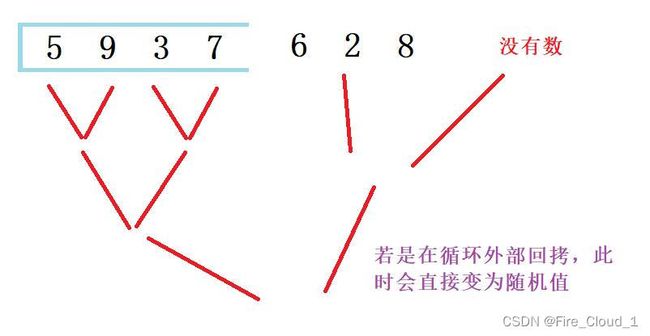
- 我们来看一下把这段数据回拷逻辑放在循环内部会怎样
- 可以看到,出现了很多随机值,这是因为每次在归并之后返回的仅仅是一组归并完后的数据,这并不完整,因此这里才会出现一个随机值
特殊情况考虑【边界的修正】
看完了归并排序的递归实现非递归实现,你认为就结束了,不,对于归并排序,我们还需要考虑其边界值
- 什么叫边界值的修正呢,我们一起来看一下
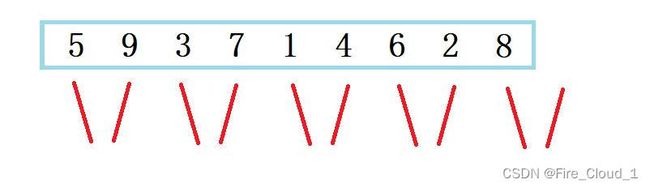
- 上面我们都是使用八个数字来完成的归并,现在我们改变一下,增加一个数字,使用9个数字,再对它们进行一个两两的归并,然后可以看到,最后新增加出来的一个数字8没有数与其一同做匹配了,那该怎么办?
- 这个时候编译器就会继续往后寻找进行一个匹对,但是这样的话数组就越界了这,这种情况的话就是右半区间根本不存在,这个时候我们其实不用去管这个数,直接跳过,到最后去归并即可
- 然后我们再来讨论一种情况,就是当这个右半区间算多了的时候,可以看到,就是以下这种情况,就算你在归并的时候右边只有一两个数,但是在继续归并下去的时候编译器还是当这个左区间和右区间的数是一样的,这个时候其实就会造成指针越界的情况
- 那这个时候应该怎么办呢?这个时候我们应该去修正一下这个右边界值
- 让我们一起来看一下具体的代码,修改的地方并不多,就两个地方
//若是归并的右区间不存在
if (begin2 >= n)
break;
//若是归并过程中右半区间多计算了,则修正一下
if (end2 >= n)
end2 = n - 1;
- 然后还有一块地方要修改的就是最后拷贝回去的这段逻辑,要放在循环内部,因为如果你放在这个循环外部的话,我们来看一种特殊情况
- 这个左半区间没有问题,但是右半区间只有三个数,少了一个,所以根据我们上面的代码逻辑【break】,右半区间不存在,所以根本就没有处理,所以在下一层归并完后原本的后面右半区间就是一个随机值,这个时候当第一次的循环结束,也就是本层的gap处理完后,回拷的时候,也会是一个随机值,这个时候就出现问题了,所以我们要将这个回拷的逻辑放在循环内部执行
- 所以当这个右半区间不存在时,就会直接break,不会执行我们这段回拷逻辑
整体代码展示
//非递归
void MergeSort_NoRecursive(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += gap * 2)
{
//[i, i + gap - 1][i + gap, i + 2 * gap - 1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = i;
//若是归并的右区间不存在
if (begin2 >= n)
break;
//若是归并过程中右半区间多计算了,则修正一下
if (end2 >= n)
end2 = n - 1;
//二路归并
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
/*
*此时跳出上面的循环后一定有一个区间已经结束
*但是还有一个区间没结束
*无需比较,直接放入另一数组即可
*/
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//最后是将每组归并完后的数据全部拷贝回去,供下一次归并使用
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2; //每次归并完gap * 2
}
free(tmp);
}
总结与提炼
本文我们主要是讲解了归并排序,说到了其具有递归和非递归两种方法,普通的大家只需要掌握递归就可以了但是对于校招来讲,你要去掌握非递归。好,七大常用的排序算法说到这里就结束了,接下去会更新其他专栏,敬请期待
最后感谢您对本文的观看,如果问题请于评论区留言或者私信我