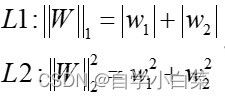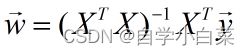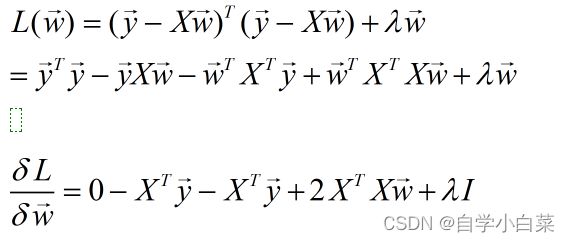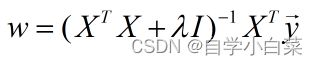深入机器学习1：详解正则表达式
深入机器学习1：详解正则表达式
前言
本系列靠很多参考资料支撑，随缘更新，主要的目的是帮我自己复习梳理一下知识，顺便分享一下自己的理解。
必备说明
本系列写起来很费劲，需要打公式，还需要自己理解。所以，如果有打错字请理解，如果有说错，请务必指出，欢迎大家一起讨论学习。
目录结构
文章目录
-
- 深入机器学习1：详解正则表达式
-
- 1. 概述：
- 2. L1与L2正则化表达式：
- 3. 逻辑回归中的正则化作用：
- 4. L1和L2正则化的区别：
- 5. 总结：
1. 概述：
正则化的主要作用就是防止过拟合，因此广义上来说，只要能够减轻过拟合的方法都可以称之为正则化手段。
本篇文章，主要探讨L1和L2正则化表达式。
2. L1与L2正则化表达式：
以二元为例，表达式分别为：
而，L1和L2正则化表达式一般用于：
new_loss = loss + L1/2
其中，loss为原来模型的损失函数
3. 逻辑回归中的正则化作用：
我们知道逻辑回归的表达式为：
其中：
y 为真实类别值
f 为预测概率值
那么，问题来了：如果没有正则化表达式来控制loss值，并且当我们的w值已经找到了合适的（比如w1 and w2），那么假设不断扩大w1 and w2，结果会怎么样？
这一部分看下面手写的内容：（后期补充：下面中的x>0的x指的是原sigmoid中的x）
即，随着w扩大，损失值居然越来越低，而我们的目标恰好又是损失值越低越好，这意味着什么？对于逻辑回归而言，如果没有正则化控制损失值，那么w值会随着训练进行，趋近于无穷大。
恰好，sklearn实现的逻辑回归，就是自带正则化的，这也证明了我们的想法。
我是在网上某视频教程看到的，当时觉得很厉害，因为我从没有这么想过，因此写下来分享给大家
4. L1和L2正则化的区别：
从MAE与MSE角度理解
不难看出，L1和L2正则化与MAE、MSE的表达式几乎一致。
而MAE与MSE有一个很大的区别：MSE具有“敏感性”。此话何解：以线性回归为例子：
假设：y为真实值，f为预测值
y - f MAE MSE
5 5 25
4 4 16
3 3 9
2 2 4
1 1 1
从上表中，可以看出，MAE之间的差值随着真实值与预测值差值的减小都没有变化（都为1），而MSE却随着差值的减小而减小（从25-16=9----16-9=7----减小）。
这句话这么理解：假设，我们的预测目标为y=w1*x + w2*x + w0，且其中w1对应的为重要特征，w2对应的为冗余特征（可有可无）。当我们的模型慢慢训练，损失值会越来越小，而由于MAE没有敏感性（即差值固定），意味着模型无论如何调整w1、w2权值（当然是往好的方向调整）收益都一样，这样当调整到一定程度，w1收敛了，w2仍然可以调整，因为它不会改变收益，这样w2值就会被调整为0。而MSE却不一样，当调整过程中，w2会因为收益变小，而停止调节，w1会因为仍然有收益而继续调节。
上面描述的有点不准确和抽象。这也是因为我也是直觉上的感官，没有从数学上去解释它，见谅，以后如果看论文看见了会补充
简而言之，L1正则化可以起到特征选择/降维的作用，L2正则化则是均衡调整权值。
从等高线和公式理解
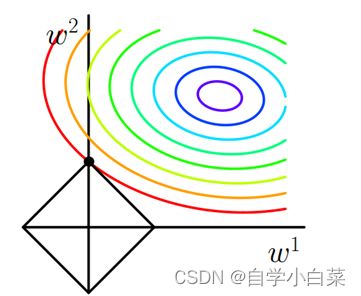
首先，以L1正则化为例子，以二维进行说明，看下图：
先对上图进行一个简单的说明，横纵坐标为两个参数，方形是L1正则项的体现，等高线是损失函数的值的等高线。
有了上面的理解后，需要补充一点就是，这个图有个问题，我们必须限制|w1|+|w2|=a，这样才可以画出方形的图像。
然后，没有正则项的时候，损失函数的最优解肯定实在等高线的中心处，但是当存在正则项时，意味着你的w1、w2参数必须满足方形的范围，因此最优解会向原点偏移，此时等高线会与方形的顶点相交，这就是加入L1正则后的最优解。
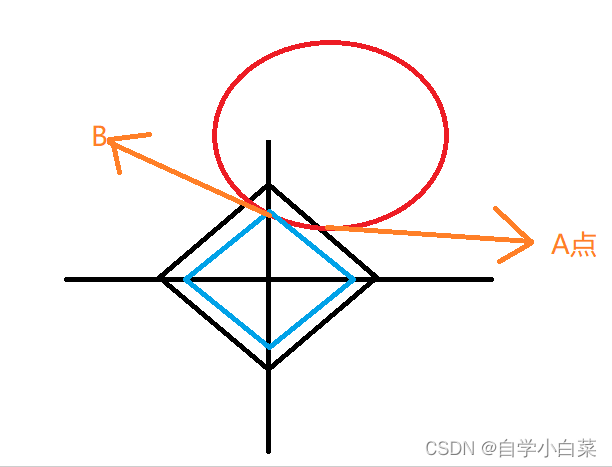
此时，你肯定会有疑问：为什么一定相交于顶点？
我这里说明一下我自己的理解：
看上图，如果等高线与方形交于A点，根据等高线的性质，那么可以转移到B点，而我们必须得明白，就是这个方形是我们自己定义的，那么意味着也可以有等高线（从公式来讲就是w1+w2=a中对a进行等比缩放操作），可以缩小到蓝色方形的位置，此时B点也是顶点。
那么，可以看出，顶点处必有一些参数值为0，这也意味着L1正则化可以实现稀疏化，或者也可以说特征选择。
L2正则化的特殊用处：解决多元线性回归中矩阵不可逆问题
最后，我想把话题回到多元线性回归问题上：
这个公式大家应该都知道，就是多元线性回归中矩阵表示最后的结果。这里是否有结果取决是否存在可逆矩阵，而正则化可以解决这个问题。
那么，是否L1、L2正则化都可以解决这个问题呢？我觉得不是，看下面的计算：
上面是根据L1正则进行的计算，不难发现，此时计算的结果没有什么大的改变，仅仅是右边多了一项λI（求导后必须含有w项才可以影响最后的结果），这没有办法影响结果。
但是，如果是L2正则化，由于此时λ乘以的相当于w平方，因此求导后还会剩下一个w，因此可以影响结果，最后算出来的结果是：
至于为什么这样求出来的矩阵一定会存在可逆矩阵，这就是线代部分的知识了，大家不清楚的话可以百度一个半正定矩阵加上单位矩阵为什么一定可逆？就可以找到解释。
5. 总结：
上面分享了我对L1、L2正则化的理解，可以说基本上把我自己看过的文章、视频里面的内容都总结出来了，希望能够帮助大家。
线代部分的知识了，大家不清楚的话可以百度一个半正定矩阵加上单位矩阵为什么一定可逆？就可以找到解释。