深入学习 GC 算法 - 标记清除算法

前言：

作者简介：热爱编程的小七，致力于C、Java、Python等多编程语言，热爱编程和长板的运动少年！

相关专栏Java基础语法，JavaEE初阶，数据库，数据结构和算法系列等，大家有兴趣的可以看一看。

有兴趣的话关注博主一起学习，一起进步吧！

1、什么是标记清除算法

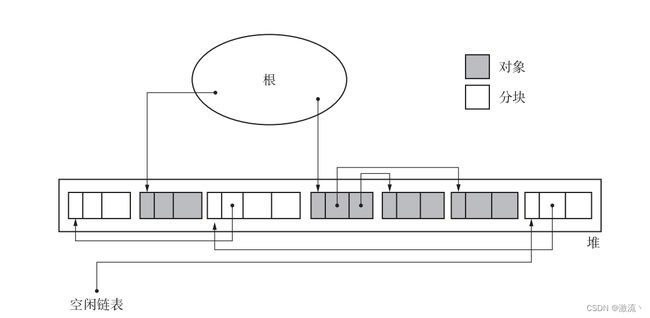
标记清除算法（Mark-Sweep Algorithm）是一种常见的垃圾回收算法，用于自动管理动态分配的内存空间。其原理如下：

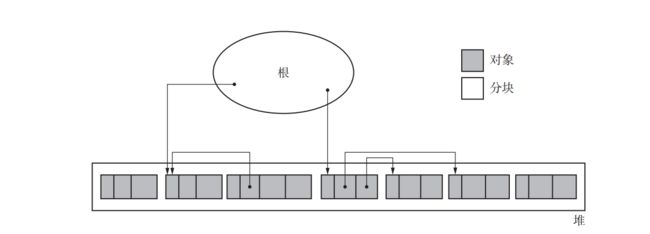
1. 标记阶段（Mark）：从根对象开始，通过引用链追踪，标记所有的活动对象。标记过程中，将活动对象的标记位设置为有效状态，表示这些对象是可达的，不会被回收。

2. 清除阶段（Sweep）：在标记阶段完成后，遍历整个内存空间，将未被标记的对象视为垃圾对象，将其所占用的内存空间释放，以便下次分配给新的对象使用。

标记清除算法通过标记和清除的过程，将不再被使用的内存空间回收，以避免内存泄漏和内存碎片的问题。然而，标记清除算法也存在一些缺点，如清除阶段会产生内存碎片，可能会导致内存分配的效率降低。

为了克服标记清除算法的缺点，还有其他更高级的垃圾回收算法被开发出来，如标记-整理算法和分代收集算法。这些算法通过不同的方式来提高垃圾回收的效率和内存利用率。

标记清除算法 mark_sweep() 函数：

mark_sweep(){
   

     mark_phase()

     sweep_phase()
}

可以看出确实分成了标记阶段和清除阶段。

2、标记清除算法的优缺点

标记清除算法（Mark-Sweep Algorithm）是一种常见的垃圾回收算法，它的优点和缺点如下：

优点：

1. 简单易实现：标记清除算法的实现相对简单，只需要进行标记和清除两个阶段的操作。

2. 可以回收循环引用的对象：标记清除算法可以回收循环引用的对象，即使这些对象之间相互引用，也能正确地标记和清除。

缺点：

1. 内存碎片问题：标记清除算法在回收垃圾对象后，会产生内存碎片，导致内存空间的利用率降低。这可能会导致后续的内存分配操作变得困难，需要进行内存碎片整理或者使用其他算法来解决。

2. 垃圾回收过程的停顿：标记清除算法在进行垃圾回收时，需要停止程序的执行，进行标记和清除操作。这会导致一段时间的停顿，可能影响程序的响应性能。

需要注意的是，标记清除算法适用于短生命周期的对象，而对于长生命周期的对象，可能会导致内存碎片问题。为了解决这些问题，可以结合其他垃圾回收算法，如标记-整理算法和分代收集算法，以提高内存利用率和垃圾回收效率。

3、标记阶段

3.1、标记阶段分析

用 mark_phase() 函数来进行标记阶段的处理，函数如下：

mark_phase(){
   
     for(r : $roots)
        mark(*r)
}

mark()函数

mark(obj){
   
     if(obj.mark == FALSE)
         obj.mark = TRUE
         for(child : children(obj))
             mark(*child)
}

标记阶段的具体步骤如下：

1. 从根节点开始，遍历程序的对象图。根节点可以是全局变量、静态变量、活动线程的栈帧等。
2. 对于遍历到的每个对象，将其标记为活动对象。可以使用标记位或者其他方式进行标记。
3. 对于每个已标记的对象，继续遍历其引用的对象，并将其标记为活动对象。这个过程可以递归进行，直到遍历完所有活动对象为止。

标记阶段的关键是通过遍历对象图，将所有活动对象进行标记。标记的方式可以根据具体实现的需求进行选择，常见的方式有使用标记位、使用颜色标记等。

标记完所有活动对象后，标记阶段就结束了。

3.2、深度优先搜索和广度优先搜索

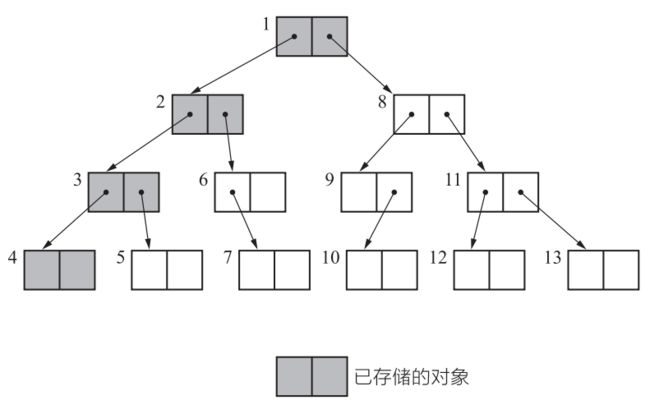
我们在搜索对象并进行标记时使用的是深度优先搜索（depth-first search）。这是尽可能从深度上搜索树形结构的方法。而且比较一下内存使用量（已存储的对象数量）就可以知道，深度优先搜索比广度优先搜索更能压低内存使用量。因此我们在标记阶段经常用到深度优先搜索。

3.3、深度优先搜索

深度优先搜索（Depth-First Search，DFS）是一种常用的图遍历算法，它从起始节点开始，沿着一条路径一直深入到无法再继续前进的节点，然后回溯到上一个节点，继续探索其他路径，直到遍历完所有节点。

深度优先搜索的基本思想是尽可能深地搜索图的分支，直到到达叶子节点或无法继续搜索的节点，然后回溯到上一个节点，继续搜索其他分支。具体步骤如下：

1. 选择一个起始节点，并将其标记为已访问。
2. 从起始节点开始，选择一个相邻且未被访问过的节点，继续深入搜索。
3. 如果当前节点没有未访问的相邻节点，则回溯到上一个节点。
4. 重复步骤2和3，直到遍历完所有节点。

深度优先搜索的特点是优先遍历深度方向，因此可以很快地到达离起始节点较远的节点。然而，由于其采用递归或栈的方式存储节点，可能会导致堆栈溢出的问题。此外，深度优先搜索并不能保证找到最短路径，因为它首先遍历到达目标节点的路径，而不是考虑路径长度。

深度优先搜索在图的遍历、迷宫求解、拓扑排序等问题中有广泛的应用。

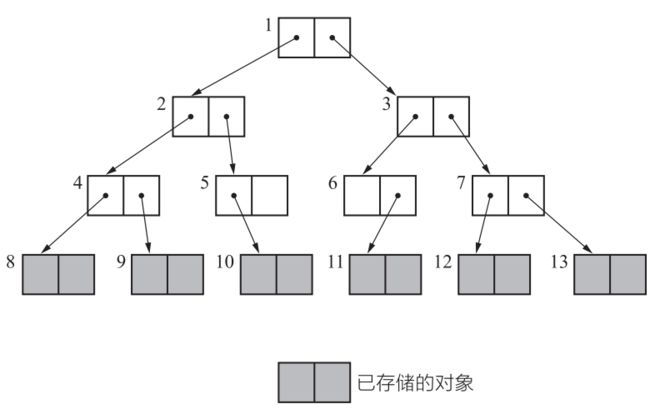
3.4、广度优先搜索

广度优先搜索（Breadth-First Search，BFS）是一种常用的图遍历算法，它从起始节点开始，逐层地向外扩展，先访问离起始节点最近的节点，然后逐渐访问离起始节点越来越远的节点。

广度优先搜索的基本思想是从起始节点开始，依次访问其所有相邻节点，然后再依次访问这些相邻节点的相邻节点，以此类推，直到遍历完所有节点或找到目标节点。

具体步骤如下：

1. 选择一个起始节点，并将其标记为已访问。
2. 将起始节点加入队列（FIFO）。
3. 从队列中取出一个节点，访问该节点，并将其所有未访问过的相邻节点加入队列。
4. 重复步骤3，直到队列为空。

广度优先搜索的特点是按照距离逐层扩展，先访问离起始节点最近的节点，然后逐渐访问离起始节点越来越远的节点。因此，广度优先搜索可以用于求解最短路径问题。此外，广度优先搜索也可以用于检测图中的环路、拓扑排序等问题。

广度优先搜索通常使用队列来存储待访问的节点，因此不会出现堆栈溢出的问题。但是，由于需要存储所有已访问过的节点，因此空间复杂度较高。

广度优先搜索在图的遍历、寻找最短路径、社交网络分析等领域有广泛的应用。

4、清除阶段

在清除阶段中，collector 会遍历整个堆，回收没有打上标记的对象（即垃圾），使其能再次得到利用。

sweep_phase() 函数

sweep_phase(){
   
     sweeping = $heap_start
     while(sweeping < $heap_end)
         if(sweeping.mark == TRUE)
             sweeping.mark = FALSE
         else
             sweeping.next = $free_list
             $free_list = sweeping
         sweeping += sweeping.size
}

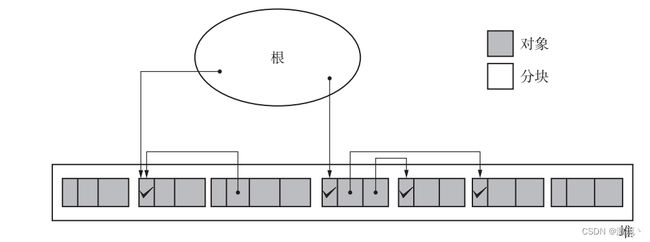
在标记阶段完成后，清除阶段的主要目的是清除未被标记的对象，即那些在程序中没有被引用的对象，并释放它们所占用的内存空间。

清除阶段的具体步骤如下：

1. 遍历整个堆内存，对于每个对象，检查其是否被标记为活动对象。

2. 如果对象被标记为活动对象，则保留它，表示它仍然被程序引用，不进行清除。

3. 如果对象没有被标记为活动对象，则将其标记为未使用的内存空间，并将该内存空间加入到空闲列表中，以便后续的内存分配使用。

4. 继续遍历堆内存中的所有对象，重复上述步骤，直到清除完所有未被标记的对象。

清除阶段的关键是通过遍历堆内存中的所有对象，将未被标记的对象进行清除。清除的方式可以是将其标记为空闲内存空间，或者直接释放其所占用的内存。

需要注意的是，清除阶段可能会引起内存空间的不连续性，即产生内存碎片。为了解决这个问题，一些优化技术如标记-整理算法、分代收集算法等可以应用于标记清除算法中。

清除阶段完成后，垃圾对象被清除，内存空间被回收，可以供程序进行新的内存分配和使用。

清除阶段结束后：

5、分配

5.1、什么是分配

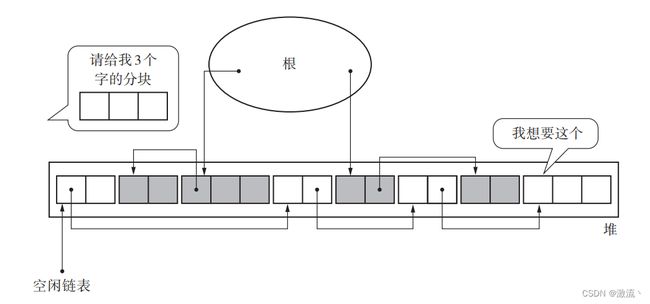
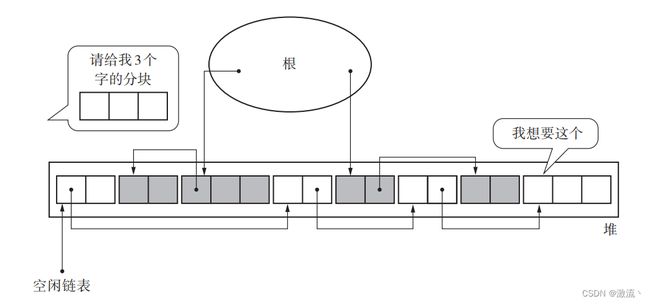
在清除阶段已经把垃圾对象连接到空闲链表了。搜索空闲链表并寻找大小合适的分块，这项操作就叫作分配。

分配函数 new_obj() 函数：

new_obj(size){
   
     chunk = pickup_chunk(size, $free_list)
     if(chunk != NULL)
         return chunk
     else
         allocation_fail()
}

new_obj()函数接受一个参数size，表示要分配的对象的大小。它调用pickup_chunk()函数来从空闲列表（free_list）中获取一个足够大的内存块。如果成功获取到内存块，则返回该内存块的指针；否则，调用allocation_fail()函数来处理内存分配失败的情况。

5.2、常见的分配算法

First-fit、Best-fit和Worst-fit是三种常见的内存分配算法，用于管理操作系统中的内存分配。它们的具体含义如下：

1. First-fit（首次适应算法）：该算法会在空闲内存块列表中找到第一个能够满足要求的内存块，并将其分配给请求的内存。这种算法的优点是简单快速，但可能会导致较大的内存碎片。

2. Best-fit（最佳适应算法）：该算法会在空闲内存块列表中找到最小的能够满足要求的内存块，并将其分配给请求的内存。这种算法的优点是可以最大限度地减少内存碎片，但可能会导致较长的搜索时间。

3. Worst-fit（最差适应算法）：该算法会在空闲内存块列表中找到最大的能够满足要求的内存块，并将其分配给请求的内存。这种算法的优点是可以减少大型内存块的浪费，但可能会导致较大的内存碎片。

6、合并

根据分配策略的不同可能会产生大量的小分块。但如果它们是连续的，我们就能把所有的小分块连在一起形成一个大分块。这种“连接连续分块”的操作就叫作合并（coalescing），合并是在清除阶段进行的。

合并的函数 sweep_phase() ：

sweep_phase(){
   
     sweeping = $heap_start
     while(sweeping < $heap_end)
         if(sweeping.mark == TRUE)
             sweeping.mark = FALSE
         else
             if(sweeping == {
   mathJaxContainer[0]}free_list.size)
                 $free_list.size += sweeping.size
             else
                sweeping.next = $free_list
                $free_list = sweeping
     sweeping += sweeping.size
}

合并函数（merge function）是垃圾回收算法中的一部分，用于合并相邻的空闲内存块，以减少内存碎片。在给定的代码中，合并函数的作用是将相邻的空闲内存块合并为一个更大的空闲内存块。

4、多个空闲链表

标记 - 清除算法中只用到了一个空闲链表，在这个空闲链表中，对大的分块和小的分块进行同样的处理。但是这样一来，每次分配的时候都要遍历一次空闲链表来寻找合适大小的分块，这样非常浪费时间。

因此，我们有一种方法，就是利用分块大小不同的空闲链表，即创建只连接大分块的空闲链表和只连接小分块的空闲链表。这样一来，只要按照 mutator 所申请的分块大小选择空闲链表，就能在短时间内找到符合条件的分块了。

标记清除算法（Mark-Sweep Algorithm）通常只需要一个空闲链表来管理空闲内存块。这个空闲链表可以是一个简单的单向链表或双向链表，用于存储空闲内存块的起始地址和大小。

在标记阶段，算法会遍历堆中的所有对象，将可达的对象进行标记。在清除阶段，算法会遍历整个堆，将未被标记的对象视为垃圾，进行清除操作。清除操作的结果是产生一些连续的空闲内存块。

在清除阶段结束后，可以将这些连续的空闲内存块组织成多个链表，每个链表对应一个特定的内存块大小范围。这样可以更有效地管理不同大小的空闲内存块，提高内存分配的效率。

例如，可以将空闲内存块按照大小划分为不同的链表，比如一个链表管理大小为4字节的内存块，另一个链表管理大小为8字节的内存块，以此类推。每个链表都有一个头指针指向链表的第一个空闲内存块，空闲内存块之间通过指针进行连接。

这样的设计可以提高内存分配的效率，因为当需要分配一块特定大小的内存时，只需要在对应的链表中查找是否有足够大小的空闲内存块即可。同时，当发生内存释放时，可以将释放的内存块插入到对应大小的链表中，以便后续的内存分配使用。

需要注意的是，多个空闲链表的设计需要维护额外的数据结构和指针，增加了算法的复杂性和内存开销。因此，在实际应用中，根据具体的场景和需求，可以根据性能和内存利用率的权衡来选择是否使用多个空闲链表。

5、BiBOP 法

BiBOP 是 "Big Bag Of Pages" 的缩写。Big Bag Of Pages是一种内存管理策略，常用于操作系统中的虚拟内存管理。它的主要思想是将内存分割成固定大小的页面（Page），并将这些页面组织成一个大的袋子（Big Bag），每个页面可以容纳一个对象或数据结构。

在BiBOP中，内存被组织成一个大的连续空间，每个页面都有固定的大小。当需要分配内存时，会从空闲页面中选择一个足够大的页面来分配。如果页面中剩余的空间不足以满足分配需求，就需要从空闲页面链表中找到一个新的页面。

BiBOP的优点是：

1. 简单高效：由于页面大小固定且连续存储，分配和释放内存的操作可以高效地进行。
2. 减少内存碎片：通过将内存划分为固定大小的页面，可以减少内存碎片的发生。

然而，BiBOP也存在一些缺点：

1. 内部碎片：由于页面大小固定，当分配的对象小于页面大小时，会导致内部碎片的浪费。
2. 需要较多的内存：为了维护空闲页面链表和页面管理信息，需要额外的内存开销。

6、位图标记

标记清除算法中的位图标记（Bitmap Marking）是一种常用的标记阶段的实现方式。在标记清除算法中，标记阶段的目标是标记所有活动对象，以便在清除阶段中清除未标记的对象。位图标记通过使用位图数据结构来表示对象的标记状态，以提高标记的效率。

位图是一个由二进制位组成的数据结构，每个位对应一个对象。位图的长度与堆内存的大小相等。初始时，位图中的每个位都被设置为0，表示对象未被标记。

在标记阶段，遍历堆中的所有对象，将已经访问过的对象的对应位设置为1，表示对象已被标记。这样，在遍历完所有对象后，位图中被标记为1的位所对应的对象就是活动对象。

使用位图标记的优点是：

1. 空间效率高：位图使用的是二进制位，可以有效地节省内存空间。
2. 访问速度快：位图中的位可以通过位运算来快速访问和修改，提高了标记的效率。

然而，位图标记也有一些缺点：

1. 需要额外的空间：位图需要额外的空间来存储标记信息，这会增加内存的使用量。
2. 对象数量受限：位图的长度与堆内存大小相等，因此，位图标记算法对于大型堆或对象数量较多的情况可能会受限。

   7、延迟清除法

延迟清除法（Deferred Sweeping）是标记清除算法的一种变体。在传统的标记清除算法中，标记和清除是依次进行的，即先标记所有的活动对象，然后再清除未标记的对象。而延迟清除法则将清除阶段延迟到下一次的标记阶段之后进行，以减少清除操作对应用程序的影响。

延迟清除法的基本原理是，在标记阶段中，只标记活动对象，而不进行清除操作。将未标记的对象标记为"待清除"状态，以便在下一次的标记阶段之后进行清除。这样可以避免在标记阶段中频繁地进行内存回收操作，减少了对应用程序的影响。

延迟清除法的优点是：

1. 减少了标记阶段的停顿时间：由于不进行清除操作，标记阶段可以更快地完成，减少了对应用程序的停顿时间。
2. 提高了垃圾回收的吞吐量：由于清除操作延迟到下一次的标记阶段之后进行，可以在一次清除操作中同时处理多个未标记的对象，提高了垃圾回收的吞吐量。

然而，延迟清除法也有一些缺点：

1. 可能会增加内存占用：由于延迟了清除操作，被标记为"待清除"状态的对象会占用一定的内存空间，增加了内存的使用量。
2. 可能会导致内存碎片：延迟清除法并没有解决内存碎片问题，仍然会产生内存碎片，可能会影响到内存的利用效率。

总的来说，延迟清除法是一种可以减少对应用程序影响的标记清除算法变体，适用于对停顿时间敏感且对内存占用要求较低的场景。