学习笔记——树上哈希

普通子树哈希

树上的很多东西都是转化成链上问题的，比如树上哈希
树上哈希，主要是用于树的同构这个东西上的
什么是树的同构？

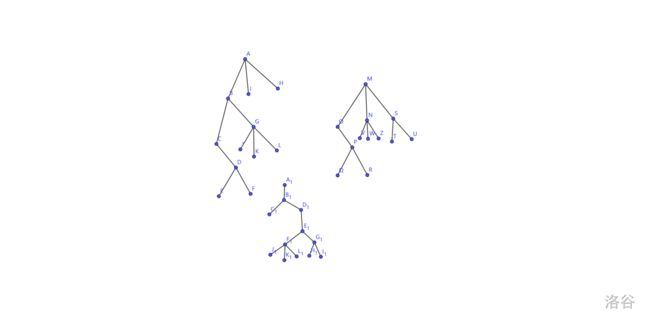
如图，不考虑节点编号，三棵树是同构的

将树转化成链，一般有两种方式：环游欧拉序与欧拉序
为了尽可能减少哈希冲突，进制位越小越好
又因为不考虑节点编号，很明显，若是采用欧拉序的话，得要记录该节点孩子数
环游欧拉序只用进入打上1，出来打上2即可搞定
小tips：欧拉序相较于环游欧拉序可能更快，请量力而行

于是，就可以采用普通的哈希方式啦！

指定范围子树哈希

如果说是将子树横着割一刀呢？
如图，是一棵树

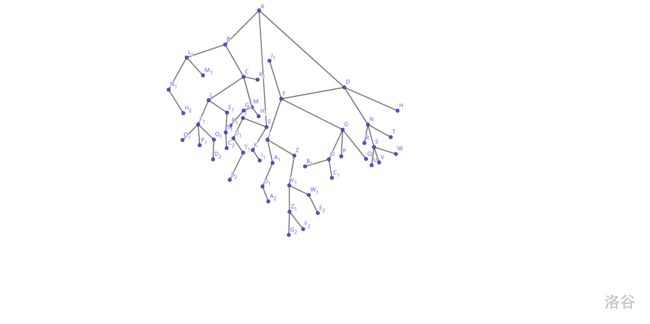
放心，就60个节点
我们考虑D节点的子树中，距离D不超过3的所有点
如图

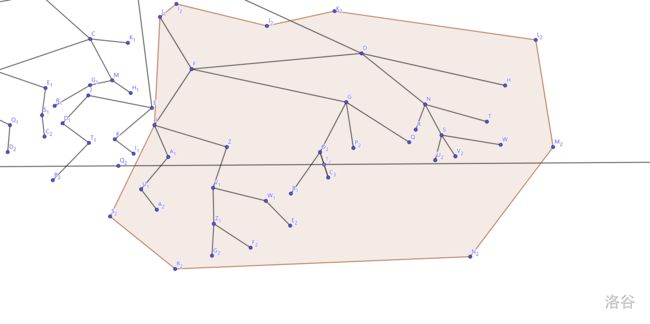
接着是环游欧拉序（考虑在某些原因的份上，我只保留D的子树）

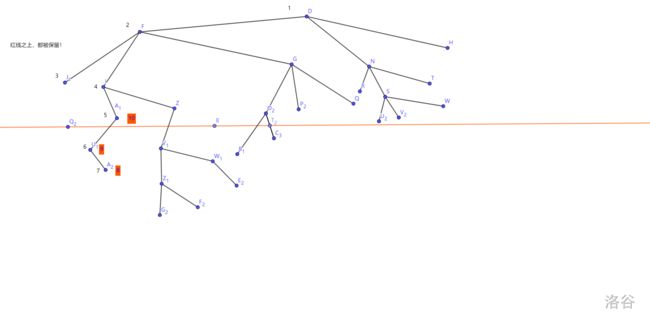
为什么我只写到10？因为作者实在太懒因为到10就够了
对于范围树上哈希，我们有两种方式——拼接与删除
因为哈希一般在取模的意义下，所以，删除是非常难以做到的~~（作者亲测过）~~
那只剩下拼接了，这个就和链上拼接一模一样了（也很像是前缀和）

模板题

题目主要考的是范围树上哈希

如果说看懂了前面的，这题就不难了。首先可以二分。因为若是$k$是答案，那么一定存在两个节点的$k$层子树是同构的。在其中任选两个对应的点，所组成的子树的子树一定是同构的
这么说显得很烦，翻译成人化就是：对于每个符合题目要求的$k$层的两个子树（就是这两个字叔同构），他们的所有子树中一定有同构的，并且层数有$0$、有$1$、有$\cdots$、有$k-1$

于是，题目就这样转化成了求是否存在同构的$k$层子树
我们可以对于每个节点，求出它的$k$层祖先，代表这个节点绝对存在$k$层子树；
再找出$k+1$曾祖先，代表这个节点的子树将要在他的祖先的子树中被删去（不被添加）
最后用一个map（建议使用gp_hash_table）统计答案
题目就这么结束了

代码

#pragma GCC optimize(1, "inline", "Ofast")
#pragma GCC optimize(2, "inline", "Ofast")
#pragma GCC optimize(3, "inline", "Ofast")
#include 
#include 
using namespace std;
namespace IO {
class input {
private:
    bool isdigit(char c) { return ('0' <= c && c <= '9'); }

public:
    input operator>>(int &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(short &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(bool &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(long &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(long long &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(__int128 &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(unsigned int &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(unsigned short &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(unsigned long &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(unsigned long long &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(unsigned __int128 &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        return *this;
    }
    input operator>>(double &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = x * 10 + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        if (!isdigit(c))
            if (c != '.')
                return *this;
        double z = 1;
        while (isdigit(c)) z /= 10., x = x + z * (c ^ 48), getchar();
        return *this;
    }
    input operator>>(long double &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = x * 10 + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        if (!isdigit(c))
            if (c != '.')
                return *this;
        double z = 1;
        while (isdigit(c)) z /= 10., x = x + z * (c ^ 48), c = getchar();
        return *this;
    }
    input operator>>(float &x) {
        x = 0;
        bool y = 1;
        char c = getchar();
        while (!isdigit(c)) y &= (c != '-'), c = getchar();
        while (isdigit(c)) x = x * 10 + (c ^ 48), c = getchar();
        if (!y)
            x = -x;
        if (!isdigit(c))
            if (c != '.')
                return *this;
        double z = 1;
        while (isdigit(c)) z /= 10., x = x + z * (c ^ 48), c = getchar();
        return *this;
    }
    input operator>>(std::string &x) {
        char c = getchar();
        x.clear();
        while (!(c != ' ' && c != '\n' && c != '	' && c != EOF && c)) c = getchar();
        while (c != ' ' && c != '\n' && c != '	' && c != EOF && c) {
            x.push_back(c);
            c = getchar();
        }
        return *this;
    }
    input operator>>(char *x) {
        char c = getchar();
        int cnt = 0;
        while (!(c != ' ' && c != '\n' && c != '	' && c != EOF && c)) c = getchar();
        while (c != ' ' && c != '\n' && c != '	' && c != EOF && c) {
            x[cnt++] = c;
            c = getchar();
        }
        return *this;
    }
    input operator>>(char x) {
        x = getchar();
        return *this;
    }
} pin;
};  // namespace IO
inline void wt(char ch) { putchar(ch); }
template <class T>
inline void wt(T x) {
    static char ch[40];
    int p = 0;
    if (x < 0)
        putchar('-'), x = -x;
    do
        ch[++p] = (x % 10) ^ 48, x /= 10;
    while (x);
    while (p) putchar(ch[p--]);
}
template <class T, class... U>
inline void wt(T x, U... t) {
    wt(x), wt(t...);
}
#define int unsigned long long
const int N = 1e5 + 7;
int n;
const int M = 2e5 + 7;
struct edge {
    int v, w, nxt;
} e[M];
int head[N], ct;
const int T = 19, K = 3;
int ll[N], x[M], nx[N];//x一定要开两倍！！！
int l[N], r[N];
int tp;
int getpw(int d) { return ll[d]; }
void addE(int u, int v, int w = 0) {
    e[++ct] = { v, w, head[u] };
    head[u] = ct;
}
void saddE(int u, int v, int w = 0) { addE(u, v, w), addE(v, u, w); }
int fa[N][T + 1];
__gnu_pbds::gp_hash_table<int, bool> cun;
void getx(int u = 1, int faa = 0) {
    l[u] = ++tp;
    x[tp] = (x[tp - 1] * K + 1);
    fa[u][0] = faa;
    for (int i = head[u]; i; i = e[i].nxt) {
        int v = e[i].v;
        getx(v, u);
    }
    r[u] = ++tp;
    x[tp] = (x[tp - 1] * K + 2);
}
int ytl[N];
typedef pair<int, int> pii;
vector<pii> vt[N];
bool chk(int mid) {
    memset(nx, 0, sizeof nx);
    cun.clear();
    memset(ytl, 0, sizeof ytl);
    for (int i = 1; i <= n; i++) vt[i].clear();
    for (int i = 1; i <= n; i++) {
        int tl = i;
        for (int j = T, k = mid; ~j; j--)
            if ((1ull << j) <= k)
                k -= (1ull << j), tl = fa[tl][j];
        if (tl == 0)
            continue;
        ytl[tl] = 1;
        tl = fa[tl][0];
        if (tl == 0)
            continue;
        // out<
        vt[tl].push_back(pii(l[i], i));
    }
    for (int i = 1; i <= n; i++) sort(vt[i].begin(), vt[i].end());
    bool flg = 0;
    for (int i = 1; i <= n; i++) {
        if (!ytl[i])
            continue;
        int lr = l[i];
        for (auto j : vt[i]) {
            int k = j.second;
            //	cout<
            (nx[i] *= getpw(l[k] - lr));
            (nx[i] += x[l[k] - 1] - (x[lr - 1] * getpw(l[k] - lr)));
            //	cout<
            lr = r[k] + 1;
        }
        (nx[i] *= getpw(r[i] - lr + 1));
        (nx[i] += x[r[i]] - (x[lr - 1] * getpw(r[i] - lr + 1)));
        if (cun[nx[i]])
            return 1;
        // cout<
        cun[nx[i]] = 1;
        //	cout<
        //	puts("");
    }
    return flg;
}
main() {
    freopen("tree.in", "r", stdin);
    freopen("tree.out", "w", stdout);
    ll[0] = 1;
    for (int i = 1; i < N; i++) ll[i] = (ll[i - 1] * K);
    IO::pin >> n;
    for (int i = 1, x, y; i <= n; i++) {
        IO::pin >> x;
        while (x--) IO::pin >> y, addE(i, y);
    }
    getx();
    for (int j = 1; j <= T; j++)
        for (int i = 1; i <= n; i++) fa[i][j] = fa[fa[i][j - 1]][j - 1];
    int l = 0, r = n - 1;
    while (l < r) {
        int mid = l + r + 1 >> 1;
        // cout<
        if (chk(mid))
            l = mid;
        else
            r = mid - 1;
    }
    printf("%llu\n", l);
}