编写Matlab代码判断多圆间的关系,并求出其交点或切点
编写Matlab代码判断两圆间的关系,并求出其交点或切点
数学定义及其判断方法
圆与圆的位置关系有五种:内含、内切、相交、外切、外离。
判断两圆的位置关系可分为三种方法:
1、利用定义,即两圆公共点的个数来判定两圆的位置关系。
| 公共点的个数 | 0 | 1 | 2 |
|---|---|---|---|
| 两圆位置关系 | 内含或外离 | 内切或外切 | 相交 |
2、利用圆心距与两圆半径之间的关系来判断两圆的位置关系。
令d为圆心距,R与r分别是两圆的半径,则有如下关系:
| 两圆位置关系 | 判断关系式(R>r) |
|---|---|
| 两圆外切 | d=R+r |
| 两圆外离 | d>R+r |
| 两圆内含 | d |
| 两圆相交 | R-r |
| 两圆内切 | d=R-r |
3、利用公共切线的条数来确定两圆的位置关系
| 公切线条数 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|
| 两圆位置关系 | 相离 | 外切 | 相交 | 内切 | 内含 |
Matlab 判断及其公式推导
此处主要利用第二方法进行判断。
公式推导下次补充。
Matlab code
main.m
clear;close all;clc;
% 随机生成n个圆心的坐标
n = 5;
Cic_Coordinate = rand(n,2)*50;
%随机生成n个圆的半径
Cic_R = 15+rand(n,1)*15;
% 画n个圆
figure;
hold on;
for i = 1:n
theta = 0:0.001:2*pi;
x = Cic_Coordinate(i,1)+Cic_R(i)*cos(theta);
y = Cic_Coordinate(i,2)+Cic_R(i)*sin(theta);
plot(x,y,'-');
end
axis equal
%判断多圆之间的关系
for i = 1:n-1
for j = i+1:n
Cic_0 = Cic_Coordinate(i,:);
Cic_1 = Cic_Coordinate(j,:);
x0=Cic_0(1); y0=Cic_0(2); r0=Cic_R(i);
x1=Cic_1(1); y1=Cic_1(2); r1=Cic_R(j);
d=sqrt((x0-x1)^2+(y0-y1)^2); %两圆心距离
if d>r0+r1
disp(['第',num2str(i),'个圆与第',num2str(j),'个圆的位置关系为:外离'])
disp(['第',num2str(i),'个圆的坐标、半径是:',num2str(x0),' ',num2str(y0),' ',num2str(r0),' ',...
'第',num2str(j),'个圆的坐标、半径是:',num2str(x1),' ',num2str(y1),' ',num2str(r1)])
elseif dCircleCross.m
function p=CircleCross(Cic_0,Cic_1,R_0,R_1)
x0=Cic_0(1);
y0=Cic_0(2);
r0=R_0;
x1=Cic_1(1);
y1=Cic_1(2);
r1=R_1;
d=sqrt((x0-x1)^2+(y0-y1)^2); %两圆心距离
k1=(y0-y1)/(x0-x1); %连接两圆心直线
b1=y1-k1*x1;
k2=-1/k1; %公共弦方程直线
b2=(r0^2-r1^2-x0^2+x1^2-y0^2+y1^2)/(2*(y1-y0));
p=[];
if d==abs(r1-r0) || d==r1+r0 %相切时的交点
xx=-(b1-b2)/(k1-k2);
yy=-(-b2*k1+b1*k2)/(k1-k2);
p=[xx yy];
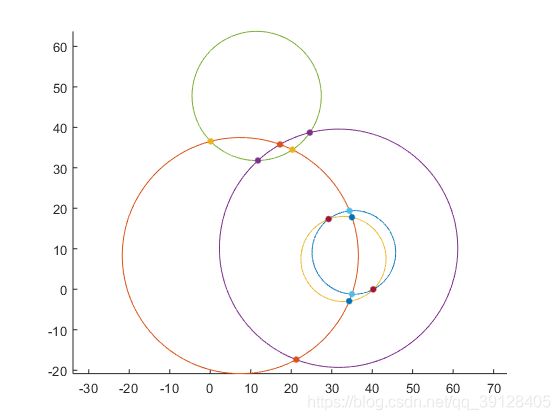
elseif abs(r1-r0)matlab运行结果图
命令行窗口运行结果:
第1个圆与第2个圆的位置关系为:相交
第1个圆的坐标、半径是:35.4742 9.1114 10.3182 第2个圆的坐标、半径是:7.4316 8.3176 29.1503
交点坐标是:34.4038 19.3739和34.986 -1.1952
第1个圆与第3个圆的位置关系为:相交
第1个圆的坐标、半径是:35.4742 9.1114 10.3182 第3个圆的坐标、半径是:32.9058 7.4804 10.5138
交点坐标是:29.2431 17.3356和40.268 -0.025588
第1个圆与第4个圆的位置关系为:内含
第1个圆的坐标、半径是:35.4742 9.1114 10.3182 第4个圆的坐标、半径是:31.6991 10.1374 29.4222
第1个圆与第5个圆的位置关系为:外离
第1个圆的坐标、半径是:35.4742 9.1114 10.3182 第5个圆的坐标、半径是:11.4653 47.7479 15.9519
第2个圆与第3个圆的位置关系为:相交
第2个圆的坐标、半径是:7.4316 8.3176 29.1503 第3个圆的坐标、半径是:32.9058 7.4804 10.5138
交点坐标是:34.3213 -2.9378和35.0024 17.783
第2个圆与第4个圆的位置关系为:相交
第2个圆的坐标、半径是:7.4316 8.3176 29.1503 第4个圆的坐标、半径是:31.6991 10.1374 29.4222
交点坐标是:17.2472 35.7656和21.2309 -17.3596
第2个圆与第5个圆的位置关系为:相交
第2个圆的坐标、半径是:7.4316 8.3176 29.1503 第5个圆的坐标、半径是:11.4653 47.7479 15.9519
交点坐标是:0.11857 36.5357和20.3068 34.4704
第3个圆与第4个圆的位置关系为:内含
第3个圆的坐标、半径是:32.9058 7.4804 10.5138 第4个圆的坐标、半径是:31.6991 10.1374 29.4222
第3个圆与第5个圆的位置关系为:外离
第3个圆的坐标、半径是:32.9058 7.4804 10.5138 第5个圆的坐标、半径是:11.4653 47.7479 15.9519
第4个圆与第5个圆的位置关系为:相交
第4个圆的坐标、半径是:31.6991 10.1374 29.4222 第5个圆的坐标、半径是:11.4653 47.7479 15.9519
交点坐标是:11.7887 31.7993和24.5955 38.6892
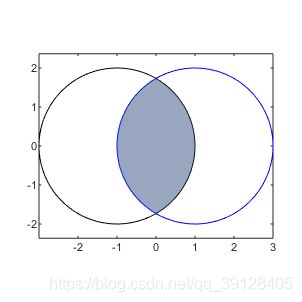
关于如何填充相交圆的面积还未写出,希望浏览本博文的能够留言补充
附 填充两圆相交区域面积的matlab,给浏览者提供下思路
以下matlab代码来自:https://www.jianshu.com/p/2f40341df631
clear;close all;clc;
x1=-1;
x2=1;
y1=0;
y2=0;
R=2;
t=linspace(0,2*pi);
X1=x1+R*cos(t);
Y1=y1+R*sin(t);
X2=x2+R*cos(t);
Y2=y2+R*sin(t);
plot(X1,Y1,'k');
hold on;
plot(X2,Y2,'b');
hold on;
t=linspace(-pi/3,pi/3);
X1=x1+R*cos(t);
Y1=y1+R*sin(t);
t=linspace(2*pi/3,4*pi/3);
X2=x2+R*cos(t);
Y2=y2+R*sin(t);
f=fill([X1,X2],[Y1,Y2],[0.2 0.3 0.5]);
set(f,'EdgeColor','none','FaceAlpha',0.5);
axis equal;
填充两圆相交面积的运行结果图: