【C语言 数据结构】串

串类型的定义

对于由多个字符（≥ 0）组成的字符串（例如 http://data.biancheng.net），数据结构单独提供了一种存储结构，称为串结构。

字符串中的字符之间具有“一对一”的逻辑关系，所以严格意义上讲，串存储结构也属于线性存储结构。和顺序表、链表、栈、队列这些线性存储结构不同的是，串存储结构专门用来存储字符串。

---

数据结构中，根据串中存储字符的数量及特点，对一些特殊的串进行了命名。

空串

• 空串指的是未存储任何字符的串，整个串的长度为 0。

• C语言中，空串可以这样表示：

  const char * str = "";
  

• 双引号表示的字符串内没有任何字符，str 就是一个空串。

---

空格串

• 空格串指的是由多个（＞0）空格字符组成的串结构，整个串的长度为包含空格字符的个数。

• 仍以 C 语言为例：

  const char * str = "     ";
  

• str 是一个包含 5 个空格字符的空格串，它的长度为 5。

• 注意：空格串和空串不同，空串中不含任何字符，而空格串中含有的是空格字符。

---

子串和主串

• 假设有以下两个串 A 和 B：

  A：shujujiegou
  B：shuju

• 在串 A 中可以找到几个连续的字符，它们和串 B 相同。我们可以这样描述它们之间的关系：A 是 B 的主串，B 是 A 的子串。

• 有些实际场景中，给定主串和子串，让我们设计算法找到子串在主串中的位置。子串在主串中的位置，指的是子串首个字符在主串中的位置。例如，串 A 为 shujujiegou，串 B 为 jiegou，通过观察可以判断 A、B 是主串和子串的关系，即在主串 A 中可以找到 B，B 的第一个字符 ‘j’ 是串 A 中的第 6 个字符，因此子串 B 在主串 A 中的位置就是 6。

---

串的表示和实现

串存储结构的具体实现方式有 3 种，分别是：

• 定长顺序存储结构

  • 与顺序存储结构类似，将字符串中的所有字符集中存放在一整块存储空间中，相邻的两个字符之间紧挨着，没有任何空隙。

  • 在 C 语言中，定长顺序存储通常用数组来实现，例如：

    char str[30] = "http://data.biancheng.net";
    

• 堆分配存储结构

  • 和定长顺序存储结构一样，堆分配存储结构也是将所有字符集中存放在一整块内存空间中，不同之处在于，堆分配存储方式使用堆空间来存储字符串。所谓堆空间，即程序执行过程中动态申请的内存空间。

  • 在 C 语言中，可以调用 malloc() 函数动态申请堆内存，动态申请的堆空间必须调用 free() 函数手动释放。

  • 和定长顺序存储结构相比，堆分配存储结构可以动态调整堆空间的大小，使用起来更加灵活。

• 块链存储结构

  • 块链存储是一种用链表存储字符串的方案，这里不再做详细介绍。

---

定长顺序存储

定长顺序存储是串结构的一种具体实现方式，简单理解就是采用固定长度的顺序表来存储字符串。

我们知道，顺序表通常使用数组来实现，数组的创建方式有两种，分别是静态数组和动态数组。以 C 语言为例，静态数组指的就是长度固定的数组，动态数组指的是调用malloc()函数创建的数组，例如：

	// 静态数组
	char str[30] = "http://data.biancheng.net"；
	// 动态数组
	char* str = (char*)malloc(30 * sizeof(char)); 

对于定义好的静态数组，它的长度是无法修改的；动态数组则不同，它的长度是可变的，定义后还可以调用 realloc() 函数扩容。

串的定长顺序存储既然用固定长度的顺序表来实现，就限定了只能用静态数组实现，不能用动态数组。

定义一个静态数组

#include
#define MAX_LEN 30
typedef char myString[MAX_LEN];
int main() {
    // 定义一个静态数组
    myString str = "http://data.biancheng.net";
    printf("%s", str);
    return 0;
}

使用定长顺序存储方式实现串结构时，要预先定义足够长的静态数组，C 语言中要保证静态数组的长度至少为「字符串长度+1」，最后一位用于存储字符串的结束标志 ‘\0’。

---

堆分配存储表示

堆分配存储是串结构的一种具体实现方案，指的是用一整块适当大小的堆内存空间来存储字符串。

所谓堆内存，就是堆区的内存空间。以 C 语言为例，程序运行时占用的内存空间会分成很多大小不等的块（区域），它们通常被称为堆区、栈区、常量区、全局数据区、代码区等。这些区域各有分工，比如全局数据区用来存储全局变量和静态变量，代码区用来存储要运行的程序指令等。

和内存的其它区域相比，堆区最大的特点就是：不会自动分配和回收，必须由程序员手动申请，使用完后再手动释放。

在 C 语言中，申请堆内存的操作可以调用malloc() 或者 calloc() 函数来完成，例如：

char * a = (char *)malloc(5 * sizeof(char));

如果 malloc() 函数执行成功，我们就申请了能存储 5 个字符的堆内存空间。

如果申请的堆内存空间不够用，还可以调用 realloc() 函数扩容，例如：

a = (char *)realloc(a, 10 * sizeof(char));

realloc() 函数执行成功，原本只能存 5 个字符的堆内存，扩容成能存储 10 个字符。

堆内存使用完后，需要手动调用free()函数释放，例如：

free(a);

---

串的堆分配存储结构，可以用如下的结构体来表示：

typedef struct {
    char* ch;
    int length;
}HString;

ch 用来指向申请好的堆空间，以便存储字符串；length 用来记录串的长度。

#include 
#include 
#include 
#define LEN1 10
#define LEN2 20
typedef struct {
    char* ch;
    int length;
}HString;
int concat(HString* str1, HString* str2) {
    int i;
    if (LEN1 < str1->length + str2->length) {
        str1->ch = (char *)realloc(str1->ch, (str1->length + str2->length + 1) * sizeof(char));
        //如果申请失败，则返回 0，表示连接失败
        if (str1->ch == NULL) {
            return 0;
        }
    }
    //合并两个串到 str1 中
    for (i = str1->length; i < str1->length + str2->length; i++) {
        str1->ch[i] = str2->ch[i - str1->length];
       
    }
    str1->ch[str1->length + str2->length] = '\0';
    str1->length += str2->length;
    return 1;
}
int main()
{
    HString str1 = { NULL,0 }, str2 = { NULL,0 };
    //创建存储"http://"的堆分配存储结构
    str1.ch = (char *)malloc(LEN1 * sizeof(char));
    strcpy(str1.ch, "http://");
    str1.length = strlen(str1.ch);
    //创建存储"http://"的堆分配存储结构
    str2.ch = (char *)malloc(LEN2 * sizeof(char));
    strcpy(str2.ch, "data.biancheng.net");
    str2.length = strlen(str2.ch);
    //连接两个串
    if (concat(&str1, &str2)) {
        printf("连接成功，新字符串为：%s", str1.ch);
    }
    else
    {
        printf("连接失败\n");
    }
    //手动释放申请的两个堆空间
    free(str1.ch);
    free(str2.ch);
    return 0;
}

---

串的块链存储表示

串的块链存储，指的是用链表存储字符串。

所谓单链表，指的是链表中的每个结点只包含一个指针，但每个结点的数据域可以存储多个元素。例如，图是用单链表存储字符串 shujujiegou，该链表的各个结点只存储了 1 个字符：

链表中，各个结点存储了 4 个字符：

当链表中各个结点存储多个（≥2）字符时，最后一个结点的数据域不一定会被占满。这种情况下，通常会用 ‘#’ 或其它的特殊字符（能与字符串区分开就行）将数据域填满。

---

也就是说，使用块链结构存储字符串，链表中的各个结点可以存储多个字符。那么问题就出现了，怎样确定各个结点存储字符的个数呢？

链表的结点存储多少个字符，会直接影响后续操作字符串的效率。例如，每个结点只存储 1 个字符，好处是方便后续做字符串做插入和删除操作（时间复杂度为 O(1) ），但字符串的存储过于分散，存储空间的利用率不高（每多一个节点，就要多申请一个指针域的空间）。

链表中各个结点存储多少个字符，需结合具体情况综合分析，比如：

• 串的长度和存储空间的大小：如果字符串很长，链表申请的存储空间有限，应尽可能地让各个节点多存储字符，提高空间的利用率；
• 程序实现的功能：实际场景中，如果需要对存储的字符串做大量的插入或删除操作，应尽可能地减少各个节点存储字符的数量，提高程序的执行效率。

#include
#include
#include
#define LINK_NNM 3//链表中各个结点存储字符的个数
typedef struct link {
    char a[LINK_NNM]; //数据域可存放 LinkNum 个字符
    struct link* next; //代表指针域，指向直接后继结点
}Link;
//初始化链表，其中head为头指针，str为存储的字符串
Link* initLink(Link* head, char* str) {
    int i, length = strlen(str);
    Link* temp = NULL;
    //根据字符串的长度，计算出链表中使用节点的个数
    int num = length / LINK_NNM;
    if (length % LINK_NNM) {
        num++;
    }
    //创建并初始化首元节点
    head = (Link*)malloc(sizeof(Link));
    head->next = NULL;
    temp = head;
    //初始化链表
    for (i = 0; i < num; i++)
    {
        int j = 0;
        for (; j < LINK_NNM; j++)
        {
            if (i * LINK_NNM + j < length) {
                temp->a[j] = str[i * LINK_NNM + j];
            }
            else
                temp->a[j] = '#';
        }
        if (i * LINK_NNM + j < length)
        {
            Link* newLink = (Link*)malloc(sizeof(Link));
            newLink->next = NULL;
            temp->next = newLink;
            temp = newLink;
        }
    }
    return head;
}
//输出链表
void displayLink(Link* head) {
    Link* temp = head;
    while (temp) {
        int i;
        for (i = 0; i < LINK_NNM; i++) {
            printf("%c", temp->a[i]);
        }
        temp = temp->next;
    }
}
int main()
{
    Link* head = NULL;
    head = initLink(head, "http://data.biancheng.net");
    displayLink(head);
    return 0;
}

---

串的模式匹配算法

字串的定位函数

所谓串的模式匹配算法，是一种专门定位子串在主串中位置的方法（方案、思想），整个定位的过程称为模式匹配。此外，在模式匹配的过程中，子串通常又被称为“模式串”。

串模式匹配的实现方法有很多种，本节先给大家讲一种最容易理解、最简单的方法，称为 BF 算法。

采用 BF 算法定位模式串在主串中的位置，就是简单粗暴的从主串的起始位置开始，不断地将模式串中的字符和主串中的字符进行对比。

具体来讲，假设对模式串 A（abcac）和主串 B（ababcabacabab）进行模式匹配，BF 算法的执行过程如下：

---

将模式串 A 与主串 B 的首字符对齐，逐个判断相对的字符是否相等

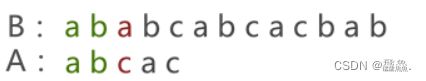
由于模式串 A 与主串 B 的第 3 个字符匹配失败，此时将模式串 A 后移一个字符的位置，采用同样的方法重新匹配

两个串依旧匹配失败，模式串 A 继续后移一个字符的位置

模式串 A 继续向后移动

模式串 A 与主串 B 共匹配了 6 次才成功，最终定位到模式串 A 位于主串 B 第 6 的位置处，整个模式匹配的过程就称为 BF 算法。

#include 
#include 
#define STR_LEN 100
typedef char myString[STR_LEN];
//串普通模式匹配算法的实现函数，其中 B是主串，A是模式串
int mate(char* B, char* A) {
    int i = 0, j = 0;
    while (i < strlen(B) && j < strlen(A)) {
        if (B[i] == A[j]) {
            i++;
            j++;
        }
        else {
            //匹配失败时，i 向后移动一位，j 重置
            i = i - j + 1;
            j = 0;
        }
    }
    //跳出循环有两种可能，i=strlen(B)说明已经遍历完主串，匹配失败；j=strlen(A),说明模式串遍历完成，在主串中成功匹配
    if (j == strlen(A)) {
        return i - strlen(A) + 1;
    }
    //运行到此，为 i==strlen(B) 的情况，模式匹配失败
    return -1;
}
int main() {
    myString B = "ababcabcacbab";
    myString A = "abcac";
    int res = mate(B, A);
    if (res == -1) {
        printf("模式匹配失败，主串中不含模式串\n");
    }
    else
    {
        printf("匹配成功，主串中定义到模式串的位置为：%d", res);
    }
    return 0;
}

---

匹配模式的改进算法

学过 BF 算法的读者应该知道，该算法的实现思想很简单，就是 “傻瓜式” 地将模式串（假定为子串的串）与主串中的字符一一匹配。KMP 算法不一样，它可以略过一些原本就不可能成功的匹配过程，提高模式匹配的效率。

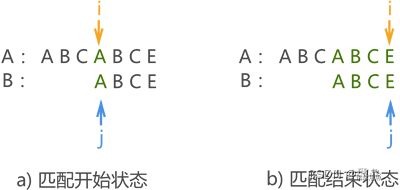
例如，对主串 A（“ABCABCE”）和模式串 B（“ABCE”）进行模式匹配，KMP 算法只需要匹配 2 次。

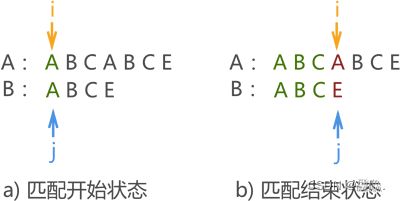
显示第一次匹配失败，从整个匹配过程可以获得的信息是：模式串中 “ABC” 和主串对应的字符相同，但模式串中的字符 ‘A’ 与 ‘B’ 和 ‘C’ 不同。这也就意味着，下次模式匹配时没必要再让串 B 中的 ‘A’ 与主串中的字符 ‘B’ 和 ‘C’ 一一匹配，它们绝不可能相等。

因此第二次模式匹配开始前，我们改变指针 j 的指向

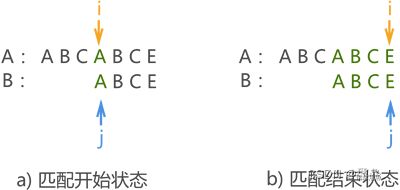
模式串直接跳过主串中的第 2、3 个字符，从第 4 个字符处开始第二次模式匹配，最终匹配成功。KMP 算法的整个匹配过程只进行了 2 次，而如果用 BF 算法需要匹配 4 次。

和 BF 算法相比，KMP 算法只需要移动指针 j 的位置，可以略过一些原本就不可能成功的匹配过程，减少匹配的次数，提高模式匹配的效率。

---

对于初学者而言，KMP 算法最大的难点是：当模式匹配失败后，如何修改指针 j 的位置。

请大家先记住一句话：指针 j 的新位置只和模式串有关，与主串无关。接下来通过一个实例，给大家演示如何只通过模式串确定指针 j 的位置。

将模式串 B 改为 “ABCAE”，第一次匹配的过程如下图所示：

匹配失败时模式串中字符 ‘E’ 前的 ‘A’ 与模式串开头的 ‘A’ 相等，因此我们可以将指针 j 指向模式串中的第 2 个字符，下次直接从 i 和 j 的位置开始匹配，这就是 KMP 算法重定位指针 j 的方法。

也就是说，模式匹配失败后指针 j 的新位置可以通过匹配失败位置前的字符计算得出。进一步讲，只要给定一个模式串，我们就可以确定匹配失败后指针 j 的新位置。

当模式串和主串进行模式匹配时，模式串中的每个字符都可能导致匹配失败，而失败后指针 j 的新位置是可以计算出来的。模式串中有多少个字符，就可以计算出多少个指针 j 的新位置，它们是一一对应的关系。我们通常会各个字符对应的 j 的新位置存储到一个数组中，并给这个数组起名为 Next 数组，数组中的值统称为 next 值。

---

模式串中各个字符对应的 next 值的计算方式是，取该字符前面的字符串（不包含自己），其前缀字符串和后缀字符串相同字符的个数再 +1 就是该字符对应的 next 值。

前缀字符串指的是位于模式串起始位置的字符串，例如模式串 “ABCD”，则 “A”、“AB”、“ABC” 都属于前缀字符串；后缀字符串指的是位于串结尾处的字符串，还拿模式串 “ABCD” 来说，“D”、“CD”、“BCD” 为后缀字符串。

注意，模式串中第一个字符对应的值为 0，第二个字符对应的值是 1 ，这是固定不变的。因此模式串 “ABCAE” 中各个字符对应的 next 值如图

各个字符对应 next 值的计算过程是：

• 第三个字符 ‘C’：在前面的字符串 “AB” 中，前缀字符串和后缀字符串相等个数为 0，0 + 1 = 1，所以字符 ‘C’ 对应的 next 值为 1。
• 第四个字符 ‘A’：在前面的字符串 “ABC” 中，前缀字符串和后缀字符串相等个数为 0，0 + 1 = 1，所以字符 ‘A’ 对应的 next 值为 1。
• 第五个字符 ‘E’：在前面的字符串 “ABCA” 中，前缀字符串和后缀字符串相等个数为 1，1 + 1 = 2，所以字符 ‘E’ 对应的 next 值为 2。

当字符 ‘E’ 匹配失败时，指针 j 指向模式串数组中第 2 个字符，即 ‘B’

---

那么，如果编写程序计算出模式串对应的 NEXT 数组呢？

可以设计这样一个算法：刚开始时令 j 指向模式串中第 1 个字符（j=1），i 指向第 2 个字符（i=2）。接下来，对每个字符做同样的操作：

• 如果 i 和 j 指向的字符相等，则 i 后面第一个字符的 next 值为 j+1，同时 i 和 j 做自加 1 操作，为求下一个字符的next 值做准备；
• 如果 i 和 j 指向的字符不相等，则执行j=next[j]修改 j 的指向，然后以同样的方法对比 i 和 j 指向的字符，以此类推。当 j 的值为 0 时，将 i 后面第一个字符的 next 值置为 1。

例如，计算模式串 “aaacd” 对应的 NEXT 数组，实现过程为：

• 前两个字符对应的 next 值分别为 0 和 1（j=1, i=2）；

• 由于 i 和 j 指向的字符相等，所以第三个字符 ‘a’ 的 next 值为 j +1 = 2，同时 i 和 j 各自加 1（此时 j=2，i=3）。

• 由于 i 和 j 指向的字符相等，所以第四个字符 ‘c’ 的 next 值为 j +1 = 3，同时 i 和 j 各自加 1（此时 j=3，i=4）。
  
• 此时 i 和 j 指向的字符不相等，执行 j = next[j] 修改 j 的指向
  
• 从上图可以看到，i 和 j 指向的字符又不相同，继续执行 j = next[j]
  

由于 j 和 i 指向的字符仍不相等，继续执行 j=next[j] 得到 j=0，字符 ‘d’ 对应的 next 值为 1。

实际上，当第一次比较 i 和 j 不相等时，意味着匹配失败位置前的最长前缀和后缀字符串不相同；执行 j=next[j] 后，i 和 j 仍不相等，意味着匹配失败位置前的次长前缀和后缀字符串也不相同，以此类推。当 j = 0 时，意味着匹配失败位置前没有相等的前缀和后缀字符串。

这里给出上述思想实现 NEXT 数组的 C 语言代码：

void Next(char* T, int* next) {
    int i = 1;
    int j = 0;
    next[1] = 0;
    //next[2]=1 可以通过第一次循环直接得出
    while (i < strlen(T)) {
        if (j == 0 || T[i - 1] == T[j - 1]) {
            i++;
            j++;
            next[i] = j;
        }
        else {
            j = next[j];
        }
    }
}

---

假设主串 A 为 “ababcabcacbab”，模式串 B 为 “abcac”，KMP 算法进行模式匹配的过程为：

• 第一次匹配如图所示，匹配结果失败，指针 j 移动至 next[j] 的位置；

• 第二次匹配如图所示，匹配结果失败，执行 j=next[j] 操作

• 第三次匹配成功

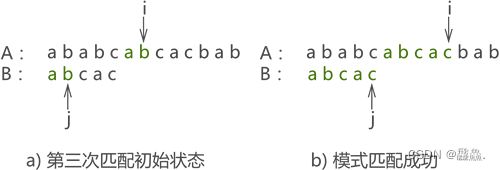
使用 KMP 算法只需匹配 3 次，而同样的问题使用 BF 算法则需匹配 6 次才能完成。

KMP 算法的完整 C 语言实现代码为：

#include 
#include 
void Next(char* T, int* next) {
    int j = 0;
    int i = 1;
    next[1] = 0;
    while (i < strlen(T)) {
        if (j == 0 || T[i - 1] == T[j - 1]) {
            i++;
            j++;
            next[i] = j;
        }
        else {
            j = next[j];
        }
    }
}
int KMP(char* S, char* T) {
    int next[10];
    int i = 1;
    int j = 1;
    Next(T, next);//根据模式串T,初始化next数组
    while (i <= strlen(S) && j <= strlen(T)) {
        //j==0:代表模式串的第一个字符就和当前测试的字符不相等；S[i-1]==T[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移
        if (j == 0 || S[i - 1] == T[j - 1]) {
            i++;
            j++;
        }
        else {
            j = next[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值
        }
    }
    if (j > strlen(T)) {//如果条件为真，说明匹配成功
        return i - (int)strlen(T);
    }
    return -1;
}
int main() {
    int i = KMP("ababcabcacbab", "abcac");
    printf("%d", i);
    return 0;
}

---