数据结构与算法:数据结构基础
目录
数组
定义
形式
顺序存储
基本操作
读取元素
更新元素
插入元素
删除元素
扩容
初始化
时机
步骤
优劣势
链表
定义
单向链表
特点
双向链表
随机存储
基本操作
查找节点
更新节点
插入节点
删除元素
数组VS链表
栈与队列
栈
定义
基本操作
1.入栈
2.出栈
队列
定义
基本操作
1.入队
2.出队
栈和队列的运用
1.栈的应用
2.队列的运用
3.双端队列
4.优先队列
散列表
定义
哈希函数
实现
读写操作
写操作
读操作
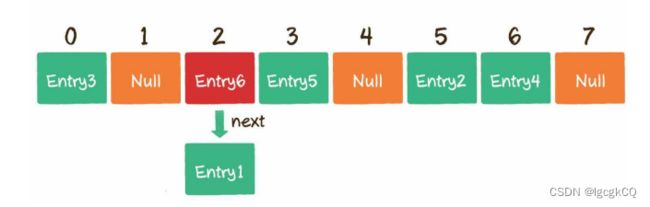
哈希冲突
解决办法
数组
定义
有限个相同类型变量所组成的有序集合,数组中每个变量都被称为元素。数组是最简单、最常见的数据结构。
形式
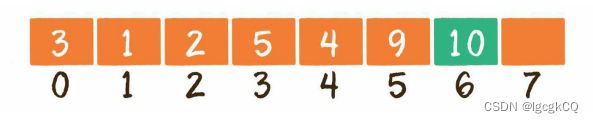
以整形数组为例:
数组中的每一个元素也有着自己的下标,只不过这个下标从0开始,一直到数组长度-1。
顺序存储
数组的另一个特点,是在内存中顺序存储,因此可以很好地实现逻辑上的顺序表。
内存是由一个个连续的内存单元组成的,每一个内存单元都有自己的地址。在 这些内存单元中,有些被其他数据占用了,有些是空闲的。
数组中的每一个元素,都存储在小小的内存单元中,并且元素之间紧密排列, 既不能打乱元素的存储顺序,也不能跳过某个存储单元进行存储
不同类型的数组,每个元素所占的字节个数也不同
基本操作
读取元素
读取元素是最简单的操作。由于数组在内存中顺序存储,所以 只要给出一个数组下标,就可以读取到对应的数组元素
注意:
通过下标读取数组,下标必须在数组长度范围内,否则会出现数组越界
示例:
int[] array = new int[]{3,1,2,5,4,9,7,2};
System.out.println(array[3]);更新元素
把数组中某一个元素的值替换为一个新值,直接利用数组下标,就可以把新值赋给该元素。
示例:
1. int[] array = new int[]{3,1,2,5,4,9,7,2};
2. // 给数组下标为5的元素赋值
3. array[5] = 10;
4. // 输出数组中下标为5的元素
5. System.out.println(array[5]);插入元素
数组的实际元素数量有可能小于数组的长度,所以存在3种情况:
1.尾部插入
是最简单的情况,直接把插入的元素放在数组尾部的空闲位置即 可,等同于更新元素的操作
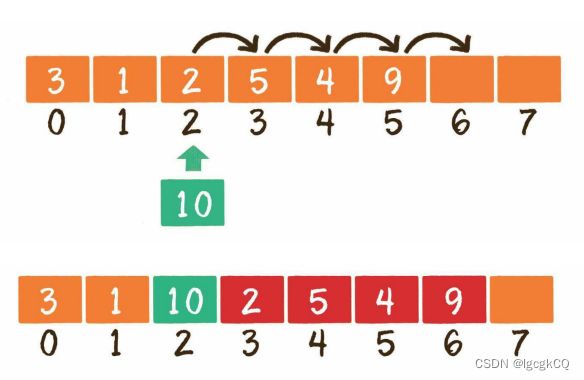
2.中间插入
由于数组的每一个元素都有其固定下标,所以不得 不首先把插入位置及后面的元素向后移动,腾出地方,再把要插入的元素放到对应 的数组位置上。
3.超范围插入
可以创建一个新数组,长度是旧数组的2倍,再把旧数组中的元素统统复制 过去,这样就实现了数组的扩容。
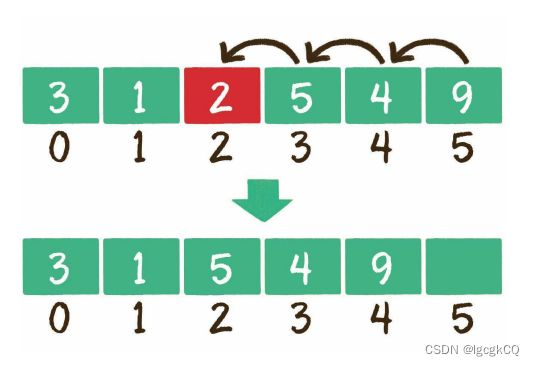
删除元素
数组的删除操作和插入操作的过程相反,如果删除的元素位于数组中间,其后 的元素都需要向前挪动1位。
/**
2. * 数组删除元素
3. * @param index 删除的位置
4. */
5. public int delete(int index) throws Exception {
6. //判断访问下标是否超出范围
7. if(index<0 || index>=size){
8. throw new IndexOutOfBoundsException("超出数组实际元素范围!");
9. }
10. int deletedElement = array[index];
11. //从左向右循环,将元素逐个向左挪1位
12. for(int i=index; i扩容
初始化
如果参数等于0,则将数组初始化为一个空数组,
如果不等于0,将数组初始化为一个容量为10的数组
时机
当数组的大小大于初始容量的时候(比如初始为10,当添加第11个元素的时候),就会进行扩容,新的容量为旧的容量的1.5倍
步骤
1:定义一个新数组,新数组的长度要比原数组增加或者减小;
2:将原数组中的元素拷贝到新数组中;
3:将原数组的名称变量指向新数组
优劣势
优点:拥有非常高效的随机访问能力,只要给出下标,就 可以用常量时间找到对应元素
缺点:由于数 组元素连续紧密地存储在内存中,插入、删除元素都会导致大量元素被迫移动,影响效率
适合的是读操作多、写操作少的场景。
链表
定义
是一种在物理上非连续、非顺序的数据结构,由若干节点组成。
单向链表
每一个节点又包含两部分,一部分是存放数据的变量data,另一部 分是指向下一个节点的指针next。
private static class Node {
int data;
Node next;
}
链表的第1个节点被称为头节点,最后1个节点被称为尾节点,尾节点的next指 针指向空。
特点
与数组按照下标来随机寻找元素不同,对于链表的其中一个节点A,我们只能根 据节点A的next指针来找到该节点的下一个节点B,再根据节点B的next指针找到下 一个节点C……
双向链表
双向链表比单向链表稍微复杂一些,它的每一个节点除了拥有data和next指 针,还拥有指向前置节点的prev指针
随机存储
链表在内存中的存储方式则 是随机存储。
内存分配方式:链表则采用了见缝插针的方式,链表的每一个节点分布在内存的不同位 置,依靠next指针关联起来。这样可以灵活有效地利用零散的碎片空间
基本操作
查找节点
在查找元素时,链表不像数组那样可以通过下标快速进行定位,只能从头节点开始向后一个一个逐步查找。
例如给出一个链表,需要查找从头节点开始的第3个节点。
第1步,将查找的指针定位到头节点
第2步,根据头节点的next指针,定位到第2个节点。
第3步,根据第2个节点的next指针,定位到第3个节点,查找完毕。
更新节点
如果不考虑查找节点的过程,链表的更新过程会像数组那样简单,直接把旧数 据替换成新数据即可。
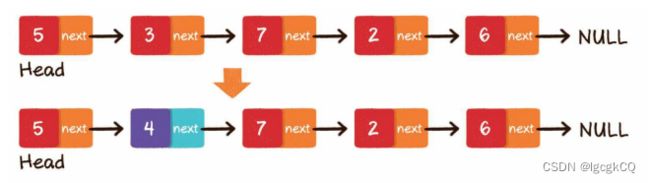
插入节点
与数组类似,链表插入节点时,同样分为3种情况:
1.尾部插入:把最后一个节点的next指针指向新插入的节点即 可
2.头部插入:把新节点的next指针指向原先的头节点;把新节点变为链表的头节点
3.中间插入:新节点的next指针,指向插入位置的节点;插入位置前置节点的next指针,指向新节点。
只要内存空间允许,能够插入链表的元素是无穷无尽的,不需要像数组那样考 虑扩容的问题
Node insertedNode = new Node(data);
if(size == 0){
//空链表
head = insertedNode;
last = insertedNode;
} else if(index == 0){
//插入头部
insertedNode.next = head;
head = insertedNode;
}else if(size == index){
//插入尾部
last.next = insertedNode;
last = insertedNode;
}else {
//插入中间
Node prevNode = get(index-1);
insertedNode.next = prevNode.next;
prevNode.next = insertedNode;
}
size++;删除元素
链表的删除操作同样分为3种情况:
1.尾部删除:把倒数第2个节点的next指针指向空即可
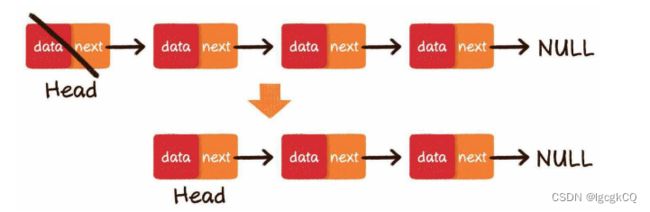
2.头部删除:把链表的头节点设为原先头节点的next指针即可
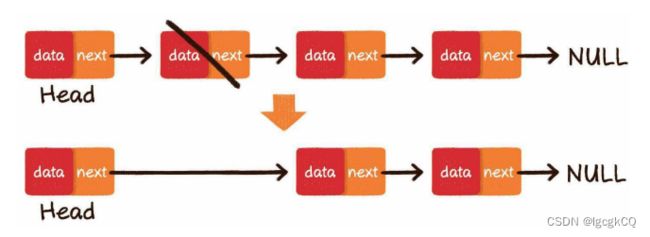
3.中间删除:把要删除节点的前置节点的next指针,指向要删除元 素的下一个节点即可。
Java拥有自动化的垃圾回收机制,所以我们不用刻意去释放被删除的节点,只要没有外部引用指向它们,被删除的节点 会被自动回收。
// 头节点指针
private Node head;
// 尾节点指针
private Node last;
// 链表实际长度
private int size;
Node removedNode = null;
if(index == 0){
//删除头节点
removedNode = head;
head = head.next;
}else if(index == size-1){
//删除尾节点
Node prevNode = get(index-1);
removedNode = prevNode.next;
prevNode.next = null;
last = prevNode;
}else {
//删除中间节点
Node prevNode = get(index-1);
Node nextNode = prevNode.next.next;
removedNode = prevNode.next;
prevNode.next = nextNode;
}
size--;数组VS链表
数组的优势在于能够快速定位元素, 对于读操作多、写操作少的场景更合适;
链表的优势在于能够灵活地进行插入和删除操 作,如果需要在尾部频繁插入、删除元素,用链表更合适一些
栈与队列
栈
定义
是一种线性数据结构。最早进入的元素存放的位置叫作栈底(bottom),最后进入的元素存放的位置叫作栈顶
数组实现:
链表实现:
基本操作
1.入栈
2.出栈
数组为例:
队列
定义
基本操作
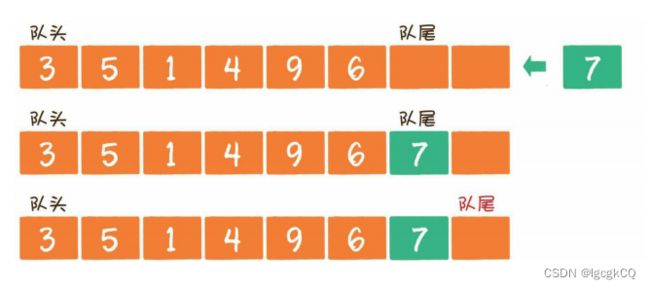
1.入队
2.出队
栈和队列的运用
1.栈的应用
实现递归的逻辑,就可以用栈来代替,因为栈可以回溯方法的调用链
面包屑导航,使用户在浏览页面时可以轻松地回溯到上一级或更上一级页面
2.队列的运用
在多线程中,争夺公平锁的等待队列,就是按照访问顺序来决定线程在队列中的次序的
3.双端队列
4.优先队列
散列表
定义
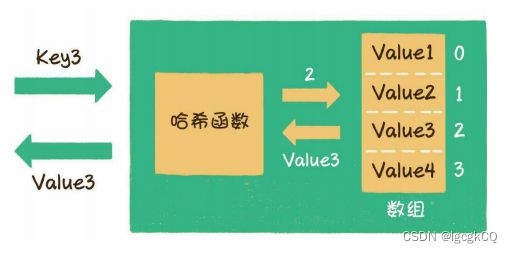
哈希函数
实现
以hashMap为例:
index = HashCode (Key) % Array.length