李宏毅深度学习self-attentin学习笔记

一、self-attention的起源

self-attention初始也是用于解决seq2seq的问题。即input是一堆序列，而output也是一段长度固定或者不固定的序列值。和RNN比较类似。多说一句，从2022年开始李宏毅老师的机器学习课程中已经删除了有关RNN和LSTM的相关内容，因为self-attention完全可以替代RNN，且效果更好。

二、self-attention网络架构

注意力的本质思想就是说，考虑上下文的输入对当前的输入的影响，然后就和人的注意力一样，将重点放在部分输入上，值得被注意的、更为相关的输入会被分配更大的权重，也意味着更被重视。
如上图所示，注意力要做的类似于上图一样，假设有4个输入，则将4个输入都都进去，然后得到4个输出b1,b2,b3,b4。这4个输出则为考虑了上下文关系之后的4个全新的向量。
当然，这里的输入也可以不是输入向量，而是中间层的隐藏向量。
在说下，这里的上下文并不是指前后2个或4个输入，而是整个sequence的信息。这里为了方便，只展示了4个输入。

我们需要重点关注如何由a得到b。如何考虑输入和上下文之后的关系呢，可以用一个相关系数$\alpha$来表征。

接下来，我们自然会思考，在self-attention中，如何自动决定两个向量之间的相关系数为多少呢，如何自动决定2个变量之间的关联性呢。
我们需要这样一个计算两个变量之间相关性的函数，如上图所示的2个黑色方框里面包围的部分。输入为2个向量，输出为2个向量之间的相关系数$\alpha$。通常使用最多的是左侧的方法，叫做Dot-product。
Dot-product是如何运作的呢，首先分别将两个输入向量和两个向量Wq,Wk进行相乘，相乘之后得到2个向量q,k。之后便可由这2个向量进行点乘dot-product得到相关系数$\alpha$。
我们看来下向量维度的变化。
输入:[N,1]，一个列向量
Wq:[M,N]，要与输入相乘，则其中一个维度必须对应
q:[M,1]
$\alpha$:一个实数scalar。

点乘的计算公式如图所示。

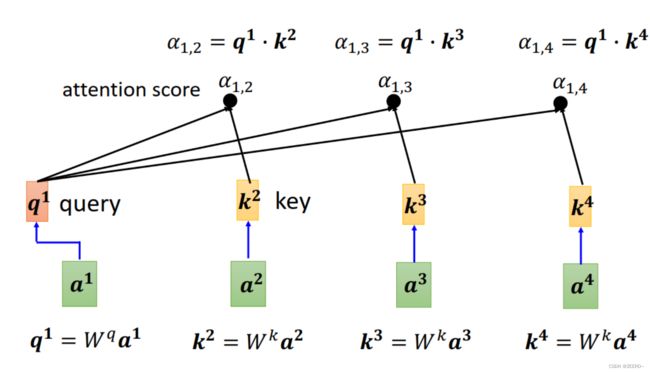
具体来说，如何分别计算出第1个与第2个向量之间的系数${\alpha }_{1,2}$，以及其他相关系数${\alpha }_{1,3},{\alpha }_{1,4}$呢。
首先，使用Wq乘以a1，再使用Wk分别乘上a2,a3,a4。这样分别得到q1,k2,k3,k4。分别进行点乘dot-production便可得到相关系数。当然，这里
其中q有个名字叫做query，而k有个名字叫做key。a1,2称为attention score。
另外，a1也可以计算自己与自己的关联性，得到${\alpha }_{1,1}$。

计算出所有的相关系数$alpha$之后，便使用softmax函数进行归一化，重新得到新的${\alpha }^{\prime }$。这里除了用softmax，也可以用其他的方法。用softmax只是为了系数之和为1，方便一些而已。

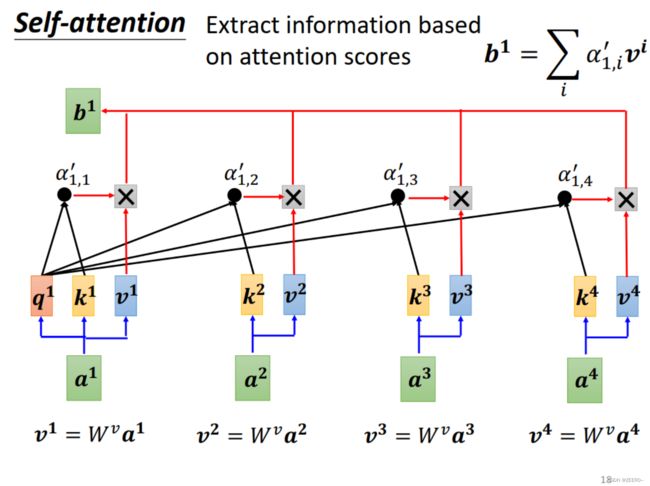
而得到了${\alpha }^{\prime }$之后，便根据${\alpha }^{\prime }$去提取出整个sequence中比较重要的信息。具体如何抽取呢？
首先，我们把a1,a2,a3,a4左侧分别都统一再乘一个向量Wv，得到v1,v2,v3,v4。之后再乘以各自对应的${\alpha }^{\prime }$，便得到了对饮的b1。
讲到这里，很多人包括我自己一开始都是很懵逼的，没事为啥要搞出3个向量Wq,Wk,Wv出来呢？要计算相关系数很容易啊，直接将两个输入向量直接做dot-production也行啊，也可以直接得到相关系数啊。另外，直接将${\alpha }^{\prime }$分别乘以输入a1-a4得到b1多好，非得搞个Wv出来增加复杂度，这样操作有什么意义吗？
答案在于复杂化可以包容更好的结果。这是我当前的理解。
计算相关系数确实可以直接将2个输入直接做dot-production，但是，先乘上Wq Wk之后再做dot-production显然已经包含了直接做dot-production的情况，将其设为乘上单位矩阵就行。Wv也是同样的道理，设为单位矩阵后便成了我们想的那种最简单的方式。
用最简单的方式固然也好，但是这样，方法就已经固定了。
使用复杂的方式的原因在于，方法不固定，就可以利用计算结果，利用梯度下降法求出比最简单的方式可能效果更好的一种方法。更容易匹配我们的训练数据。

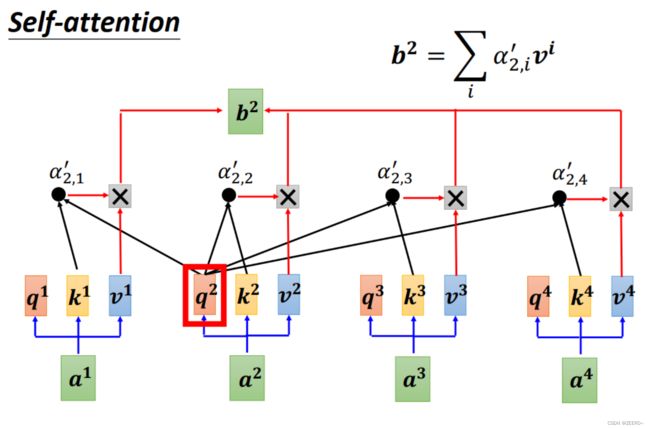
同样，要计算出b2也是一样的道理。需要额外值得说明额是，b1,b2,b3,b4并不是先计算b1,再计算b2这种。而是一次性同时被算出来的。

我们如果从矩阵运算的角度来理解self-attention，每个输入a都会生成qkv三个向量，统一起来如上图所示。
Wq,Wk,Wv的系数都是被learning出来的。其中I表示由4个输入拼接而成的矩阵。

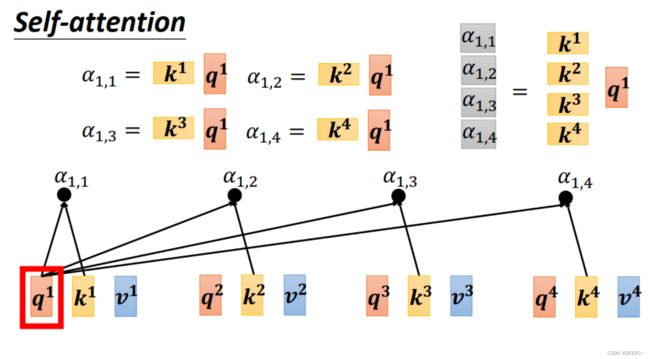
而q和k做inner product/dot production的过程也可以看作是矩阵的乘法。



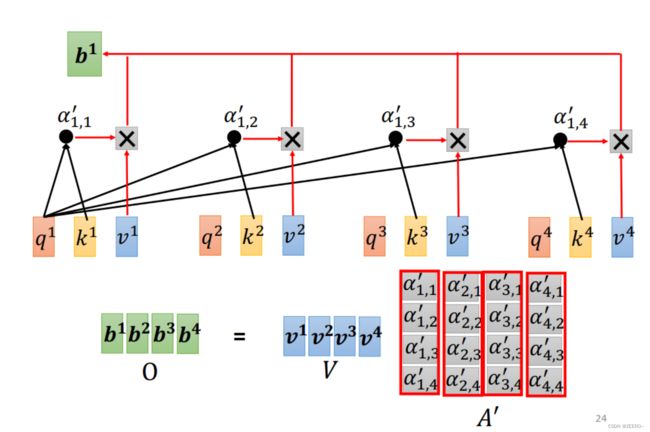
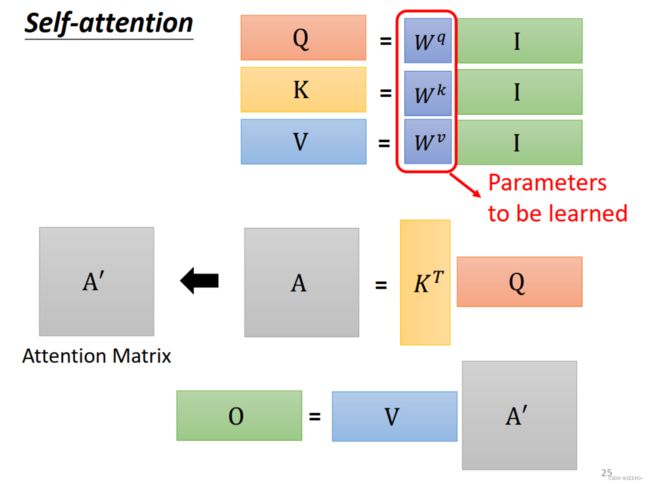
整个self-attention的过程如上图所示，本质上就是一系列的矩阵乘法运算。其中A'也叫做attention matrix.整个过程的输入是a1,a2,a3,a4，输出是b1,b2,b3,b4，而整个过程中需要学习的参数只有Wq,Wk,Wv。

三、multi-head self-attention

为什么会有multi-head self-attention呢？因为前面有说过，相关其实有很多种情况都是相关，不能只有一种形式。因此在NN中，可以在多个地方定义相关的类型。

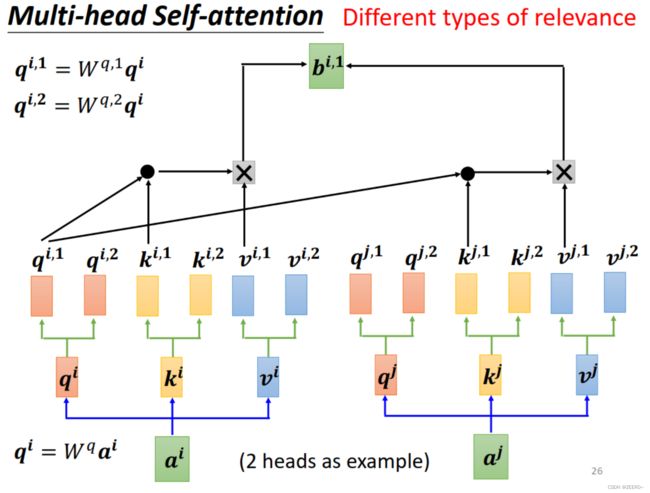
其中，qi分别乘上2个矩阵得到qi1和qi2。区分出1和2类别后，1类的分别做self-attention得到bi1，2类的再一起做self-attention得到bi2。

得到bi1和bi2之后可以再将其接起来，得到新的bi。

四、positional encoding

上面讲述了self-attention之后，我们可以看下对于a1而言，a2,a4有任何关于位置上的差别吗？没有，把a2,a4调换位置好像也没有所谓。
问题在于，我们前面讲述的模型其实是缺了一个信息的，这个信息就是位置信息。上面的可以概括为天涯若比领，所有位置上的输入位置关系是一模一样远的。
这样做可能会存在一些问题。解决的方法叫做positional encoding。

解决的方法就是为每个位置设定一个vector,ei。等于告诉self-attention位置信息，可以清楚知道哪个输入属于哪个位置。
positional encoding可以根据data学习出来，也可以人工设定，目前仍然是一个尚待研究的问题。

五、pytorch实现