伪逆学习自动编码器射频干扰去除 Radio frequency interference mitigation using pseudo-inverse learning auto-encoders

Radio frequency interference mitigation using pseudo-inverse learning auto-encoders [RAA 2020]

[pdf]

RAA : Research in Astronomy and Astrophysics 

 【推荐阅读：CSDN 博客】深度学习射频干扰消除网络：Deep residual detection of Radio Frequency Interferencefor FAST

目录

Abstract

Introduction

Pseudo-inverse Learning Auto-encoder (PILAE)

PILAE-based RFI Mitigation

Experiments and Results

1  Experiment Data

2  PILAE Hyper Parameter Tuning

3.  PILAE Model Performance and Robustness

Discussion and Conclusions 

---

Abstract

Radio frequency interference (RFI) is an important challenge in radio astronomy. RFI comes from various sources and increasingly impacts astronomical observation as telescopes become more sensitive. In this study, we propose a fast and effective method for removing RFI in pulsar data. We use pseudo-inverse learning to train a single hidden layer auto-encoder (AE). We demonstrate that the AE can quickly learn the RFI signatures and then remove them from fast-sampled spectra, leaving real pulsar signals. This method has the advantage over traditional threshold-based filter method in that it does not completely remove contaminated channels, which could also contain useful astronomical information.

射频干扰 (RFI) 是射电天文学面临的一个重要挑战。RFI 的来源多种多样，随着望远镜灵敏度的提高，它对天文观测的影响也越来越大。在本研究中，提出了一种快速有效的去除脉冲星数据中 RFI的方法。本文使用伪逆学习来训练单隐层自动编码器 AE。本文证明了 AE 可以快速学习 RFI 特征，然后从快速采样的光谱中去除它们，留下真正的脉冲星信号。与传统的基于阈值的滤波方法相比，该方法的优点在于没有完全去除污染通道，但污染通道也可能包含有用的天文信息。

Introduction

The impact of radio frequency interference (RFI) in radio astronomy is becoming more significant as human activity flourishes and radio telescopes become more sensitive. As one of the most sensitive single-dish radio telescopes, the Five-hundred-meter Aperture Spherical radio Telescope (FAST) is particularly susceptible to RFI, which comes from many different sources, such as terrestrial signals, cellphone stations, airplanes, and radar (Fridman & Baan 2001). Man-made RFI usually exists in a narrow stationary frequency range or in the form of short impulsive signals. Sometimes, satellites will generate RFI that changes over time due to Doppler shifting. Impulsive time-domain RFI can be identified by taking running-statistics on the signal time series.

随着人类活动的频繁和射电望远镜的灵敏度的提高，无线电频率干扰 (RFI) 对射电天文学的影响越来越显著。作为最敏感的单天线射电望远镜之一，500 米口径球面射电望远镜 (FAST) 特别容易受到来自许多不同来源的 RFI 的影响，如地面信号、手机站、飞机和雷达 (Fridman & Baan 2001)。人工射频干扰通常存在于较窄的平稳频率范围内或以短脉冲信号的形式存在。有时，由于多普勒频移，卫星会产生随时间而变化的 RFI。脉冲时域 RFI 可以通过对信号时间序列进行运行统计来识别。

Many techniques have been proposed to excise RFI from astronomical data, such as reference antennas for RFI signal subtraction (Barnbaum & Bradley 1998; Briggs et al. 2000; Finger et al. 2018), spatial filtering techniques (Leshem et al. 2000; Ellingson & Hampson 2002; Smolders & Hampson 2002; Boonstra et al. 2002; Kocz et al. 2010; Keane et al. 2018), threshold-based signal filter method (Baan et al. 2004; Offringa et al. 2010; Nita & Gary 2010; Peck & Fenech 2013), machine-learning or deep-learning methods (Burd et al. 2018; Czech et al. 2018; Yang et al. 2020). Eatough et al. (2009) introduced a zero-DM filter that utilized a signature of wide-band impulsive RFI and removed them effectively in pulsar data. Pen et al. (2009) proposed the singular value decomposition (SVD) RFI mitigation method. An RFI signal is usually stronger than an astronomical signal. As a result, the largest SVD eigen values and vectors often represent RFI and the persistent structure in the data, such as the bandpass. By setting these eigenvalues to zero when reconstructing the data, we can possibly remove strong RFIs and bandpass. A recent review by An et al. (2017) introduced all kinds of RFI mitigation strategies.

目前已经提出了许多从天文数据中提取射频干扰的技术，如用于射频干扰信号消除的参考天线(Barnbaum & Bradley 1998;Briggs et al. 2000年;Finger et al. 2018)、空间滤波技术 (Leshem et al. 2000;Ellingson & Hampson, 2002;Smolders & Hampson 2002;Boonstra et al. 2002;Kocz et al. 2010;Keane et al. 2018)，基于阈值的信号滤波方法 (Baan et al. 2004;Offringa et al. 2010;Nita & Gary 2010;Peck & Fenech 2013)、机器学习或深度学习方法 (Burd et al. 2018;Czech et al. 2018;Yang et al. 2020)。Eatough et al. (2009) 引入了一种利用宽带脉冲 RFI 特征的 zero-DM 滤波器，并在脉冲星数据中有效地去除它们。Pen et al. (2009) 提出了奇异值分解(SVD) RFI 减缓方法。射频干扰信号通常比天文信号强。因此，SVD 的最大特征值和向量往往代表数据中的 RFI 和持久结构，如频带通。通过在重构数据时将这些特征值设为零，可以去除强射频信号和带通。An et al. (2017) 最近的一篇综述介绍了各种 RFI 消除策略。

An et al. 2017:

Radio Frequency Interference Mitigation [CAA 2017]

Yang et al. 2020：(深度学习)

Deep residual detection of Radio Frequency Interference for FAST

[paper in MNRAS (2区) 2020] [CSDN 博客]

The FAST (Nan et al. 2011) is currently being commissioned (Jiang et al. 2019) and the 19-beams receiver has been installed (Li et al. 2018). Searching for new pulsars is one of the main scientific objectives of FAST, at present, it has discovered dozens of new pulsars (Qian et al. 2019; Zhang et al. 2019).

FAST 目前正在服役， 19 波束接收器已经安装。寻找新的脉冲星是 FAST 的主要科学目标之一，目前已经发现了几十个新的脉冲星。

The FAST pulsar data includes two significant components: (1) the bandpass of the data; and (2) RFI, both wideband and narrow-band. These two components are always or frequently reoccurring in the data. Conversely, real pulsar signals are often weaker than RFI and uncommon in the data. RFI excision is very important for pulsar search. However, there are two problems in the traditional methods of RFI mitigation, one is the low efficiency and the other is incomplete pulsar signal. When using threshold-based method to mitigate RFI, the pulsar signal will be influenced.

Therefore, we could use machine learning techniques to model the signature of bandpass and RFI from a large segment of data, and then apply these models to fit and reconstruct data. Because these models are constructed from common reoccurring signatures, they could potentially catch and clean common RFI. Following these ideas, we experimented to remove RFI from pulsar data using the unsupervised machine learning method (i.e. pseudo-inverse learning auto-encoder). Our method is in theory similar to the SVD method. We use auto-encoder to learn the primary components of data. Because the most significant components of the raw data are the spectral bandpass and RFI, the recomposed data mainly contains these signals. When we subtract the recomposed data from the raw input data, we leave what is uncommon, (i.e., astronomical signals).

FAST 脉冲星数据包括两个重要组成部分: (1) 数据带通; (2) RFI，包括宽带和窄带。这两个组件总是或经常在数据中重复出现。相反，真实的脉冲星信号通常比 RFI 弱，在数据中不常见。RFI 消除对脉冲星搜索非常重要。然而，传统的 RFI 消除方法存在两个问题，一是效率低，二是脉冲星信号不完整。当采用基于阈值的方法来抑制 RFI 时，脉冲星信号会受到影响。

因此，我们可以利用机器学习技术从大量数据中对带通和 RFI 的 特征 (signatures)  进行建模，然后应用这些模型对数据进行拟合和重构。因为这些模型是由常见的重复出现的 特征 (signatures) 构建的，所以它们有可能捕获和清除常见的 RFI。按照这些思路，我们尝试使用无监督机器学习方法(即伪逆学习自动编码器) 从脉冲星数据中去除 RFI。我们的方法在理论上与 SVD 方法相似。使用自动编码器来学习数据的主要组成部分。由于原始数据中最重要的成分是频谱带通和 RFI，重构数据主要包含这些信号。当从原始输入数据中减去重组后的数据时，留下了不常见的数据 (即天文信号)。

Our proposed method has two advantages: (1) the influence of pulsar signal is reduced by adjusting the number of neurons in the hidden layer and regularization parameter; and (2) by training the auto-encoder with pseudoinverse learning, the algorithm can run efficiently.

该方法具有两个优点:

(1) 通过调整隐层神经元数量和正则化参数来减小脉冲星信号的影响;

(2) 通过伪逆学习对自动编码器进行训练，算法能够有效地运行。

Pseudo-inverse Learning Auto-encoder (PILAE)

Pseudo-inverse learning (PIL) was proposed by Guo & Lyu (2001) and Guo & Lyu (2004). Wang et al. (2017) used pseudo-inverse learning for training stacked auto-encoder to classify astronomical spectrum and recover defective spectra. The training speed of this method is fast because there is only feed-forward propagation in PILAE. Because of the heavy burden of FAST data storage, it is particularly important to propose rapid computational method to eliminate RFI. Therefore, we have made some improvements to the traditional PILAE method. It can rapidly remove RFI while retaining the celestial signal. The training set is , the ith vector can be described as: . is a column vector. So, the steps of pseudo inverse learning to train the auto-encoder can be concluded as follows:

伪逆学习 (Pseudo-inverse learning, PIL) 由 Guo & Lyu(2001) 和 Guo & Lyu(2004) 提出。Wang et al.(2017) 使用伪逆学习来训练叠式自编码器对天文光谱进行分类并恢复有缺陷的光谱。该方法的训练速度快，因为在 PILAE 中只存在前馈传播。由于 FAST 数据存储的沉重负担，提出快速计算方法来消除 RFI 尤为重要。因此，本文对传统的 PILAE 方法进行了一些改进。它可以在保留天体信号的同时快速去除 RFI。训练集为 ，第 i 个向量可以描述为: 。是一个列向量。

训练自编码器的伪逆学习步骤可归纳为以下几步：

  

Step 1: the number of hidden layer neurons setting 隐藏层个数

The rank of the input matrix is used to decide the number of hidden layer neurons. A singular value decomposition is applied to the input matrix:

, (1)

where matrices and are orthogonal matrices, is a diagonal matrix. The diagonal elements are the eigenvalues of the input matrix . The number of non-zero elements is the rank r of the matrix:

(2)

通过输入矩阵的秩来确定隐层神经元的个数。对输入矩阵进行奇异值分解 (1)；其中矩阵 and 是正交矩阵，是对角矩阵。对角元素是输入矩阵的特征值。非零元素的个数为矩阵  的秩 r，即公式 (2)。

The number of hidden layer neurons p is set to be less than the dimension n of the input matrix for learning the features of the training data. It also can avoid identity mapping and complex calculation of high dimensions. If the number of hidden layer neurons is too small, then this will lead to large reconstruction errors and the original data feature missing. The parameter p is related to the rank of the input matrix r and the dimension of the input matrix n. At the same time, we should be aware of the feature learning of the original data and the model reconstruction error. So, the value of p is set to be between the number of samples and the rank:

p = r + α(n − r), α ∈ (0, 1], (3)

where the parameter α is an empirical parameter to set the number of hidden neurons. If the auto-encoder input matrix is full rank, then the rank r of the input matrix is equal to the dimension n of the input data. We then utilize the dimension reduction to set the value of the number of hidden layer neurons p (β is empirical parameter) to

p = βr, β ∈ (0, 1]. (4)

When removing RFI, we can set the number of hidden layer elements based on experimental experience, which can improve the efficiency of the algorithm without calculating the rank of the input matrix.

设置隐层神经元数量 p 小于输入矩阵的维数 n，用于学习训练数据的特征。它还可以避免单位映射和复杂的高维计算。如果隐层神经元数量过少，则重构误差较大，原始数据特征缺失。参数 p 与输入矩阵的秩 r 和输入矩阵的维数 n 有关。同时要注意原始数据的特征学习和模型重构误差。因此，p 的值设为样本个数与秩之间，即公式 (3)；其中 α 为经验参数，用于设置隐藏神经元的数量。如果自动编码器的输入矩阵满秩，则输入矩阵的秩 r 等于输入数据的维数 n。

本文利用降维，设隐层神经元数 p (β为经验参数) 为 (4)。

在去除 RFI 时，可以根据实验经验设置隐层元素的数量，这样可以提高算法的效率，而不需要计算输入矩阵的秩。

Step 2: encoder weight initialization () 编码器权重初始化

Utilizing random value (zero median and unit variance) to initialize the encoder weight. Therefore, the input matrix can map n dimension data to p dimension through encoder weight, and the output of the hidden layer is

.     (5)

利用随机值 (零中位数和单位方差) 初始化编码器权重。因此，输入矩阵可以通过编码器权值将 n 维数据映射到 p 维，隐层输出为 (5)。

Step 3: decoder weight calculation () 解码器权重计算

The loss function of the auto-encoder is

, (6)

where symbol Wd is the decoder weight of the autoencoder. To avoid overfitting, L2 norm is added to the loss function, which thus can be written as

. (7)

λ is the regularization parameter, which can reduce the influence on the celestial signal when removing the RFI. Taking the derivative of Equation (7) and the equation can be expressed as

. (8)

Therefore, the decoder weight can be expressed as

. (9)

自动编码器的损耗函数为 (6)；其中， 是自动编码器的解码器权重。为避免过拟合，在损失函数中加入 L2 范数，可表示为 (7)；其中 λ 为正则化参数，在去除 RFI 时可以减小对天体信号的影响。对式 (7) 求导，可表示为 (8)。因此，解码器权重可以表示为 (9)。

Step 4: the raw data reconstruction. 数据重建

After this calculation, we can obtain the reconstruction data. H is the output of the hidden layer, and Wd is the decoder weight. O is the recomposed data, which mainly contain the spectral bandpass and radio interference signals as

. (10)

经过这个计算，我们可以得到重建数据。 为隐含层的输出， 为解码器权值。 为重组后的数据，主要包含谱带通和无线电干扰信号为 (10)。

PILAE-based RFI Mitigation

We utilize one basic auto-encoder (AE) to mitigate the RFI. The network contains an input layer, a hidden layer, and an output layer. Although the input data and output data tend to be consistent in AE, there are still reconstruction errors because of data dimensionality reduction through the hidden layer. In general, the radio interference signal is much stronger than the pulsar signal in the data. Therefore, the output layer mainly outputs RFI and bandpass signals. We trained the model by pseudo-inverse learning. The model can run efficiently because it does not need back propagation.

Our algorithm contains the following four steps (the algorithm flow chart is shown in Fig. 1):

本文使用一个基本的自动编码器 (AE) 来减轻射频干扰。网络包含一个输入层、一个隐藏层和一个输出层。虽然声发射中输入数据和输出数据趋于一致，但由于隐层降维，数据仍存在重构误差。一般来说，数据中的无线电干扰信号要比脉冲星信号强得多。因此，输出层主要输出 RFI 和带通信号。本文通过伪逆学习来训练模型。模型可以有效地运行，因为它不需要反向传播。

本文算法包含以下四个步骤(算法流程图如图 1 所示)：

Step 1: normalizing the input data 输入数据规范化

The input data is a two-dimensional matrix (4096 × 4096), where each row represents different time data of the same frequency band, and each column represents different frequency data of the same time band. We normalize the input data value to between 0 and 1.

输入数据为一个二维矩阵 (4096 × 4096)，每一行代表同一频带的不同时间数据，每一列代表同一频带的不同频率数据。本文将输入数据值规范化为 0 到 1 之间。

Step 2: calculating the encoder weights 初始化编码器权重

We randomly initialize the encoder weight, and the weight value satisfies the Gaussian distribution with a mean value 0 and variance 1. In the traditional PIL algorithm, the pseudo-inverse of the input matrix is used as the weight of the encoder. We randomly initialize the weight of encoder to extract random features from input data, which can also be regarded as adding noise to data and improve the efficiency of RFI mitigation.

随机初始化编码器权值，权值满足均值为 0，方差为 1 的高斯分布。传统的 PIL 算法采用输入矩阵的伪逆作为编码器的权值。本文随机初始化编码器的权值，从输入数据中提取随机特征，这也可以看作是给数据添加了噪声，提高了 RFI 抑制的效率。

Step 3: compute the input and output of the hidden layer 计算输入和输出的中间隐藏层

The input of the hidden layer is calculated through the input matrix and the weight of the encoder (Eq. (5)), and computed the output of the hidden layer using activation function (sigmoid function).

通过输入矩阵和编码器的权值 (Eq.(5)) 计算隐含层的输入，利用激活函数 (sigmoid函数) 计算隐含层的输出。

Step 4: reconstruct cleaned data 重构清晰数据

At first, we calculate the weight of the decoder according to Equation (9). Then, according to Equation (10), we can obtain the output matrix (O), which is the reconstruction of the input data. The recomposed data mainly contains RFI data. Thus, we use Equation (11) to remove RFI from raw data as

R = X − O, (11)

where R is the cleaned data after bandpass and RFI has been removed, X is the original data.

我们首先根据式 (9) 计算解码器的权值，然后根据式 (10) 得到输出矩阵 (O)，它是输入数据的重构。重组后的数据主要包含 RFI 数据。因此，我们使用式 (11) 从原始数据中去除 RFI，其中 R 为去掉带通和 RFI 后的清理数据，X 为原始数据。

Experiments and Results

1  Experiment Data

We use FAST ultra-wide-band (UWB) receiver data to test the validity of the model. The FAST ultra-wide-band receiver was installed on FAST from 2016 to 2018 for testing purposes. During that time, it was used for pulsar searches in drifting and tracking mode and discovered dozens of new pulsars. The UWB receiver operates in 270– 1800 MHz frequency range with an effective system temperature in the range of 60–120 K. We use it to sample spectrum in 200µs intervals. In each interval, we collect two spectra, one with 4096 channels in 0–1 GHz frequency range, one with 4096 channels in 1–2 GHz frequency range. Not all frequency channels in the data contain useful astronomical data, but some of them are occasionally contaminated by broad-band time-domain RFI and narrow-band frequency-domain RFI, which reduced their effectiveness in detecting weak pulsars. In this experiment, we use four 0–1 GHz FAST UWB pulsar data for testing. The four pulsar data contain real pulsars, which we use to demonstrate how the PILAE method removes bandpass and narrow-band RFI without subtracting the pulsar signal. The pulsars are J2112+4059, J2113+4644, J0659+1414 and J2006+4101. Pulsar J2112+4059, J0659+1414 and J2006+4101 have strong interference signals, while pulsar J2113+4644 has strong pulsar signals and weak interference signals.

本文使用 FAST 超宽带 (UWB) 接收机数据来测试模型的有效性。FAST 超宽带接收器于 2016 年至 2018 年安装在 FAST 上进行测试。在那段时间里，它被用来以漂移和跟踪的方式搜索脉冲星，并发现了几十个新的脉冲星。UWB 接收机工作在 270 - 1800 MHz 频率范围内，有效系统温度在60-120 K 范围内。我们用它在 200µs 的间隔内对光谱进行了采样。在每个间隔中，采集两个频谱，一个是 0-1 GHz 频率范围内的 4096 个通道，一个是 1-2 GHz 频率范围内的 4096 个通道。数据中并非所有的频段都包含有用的天文数据，但其中一些频段偶尔会受到宽带时域 RFI 和窄带频域 RFI 的污染，降低了它们探测弱脉冲星的效率。

本实验中使用 4 个 0-1 GHz FAST UWB 脉冲星数据进行测试。这四组脉冲星数据包含真实的脉冲星，我们用它们来演示 PILAE 方法如何在不减去脉冲星信号的情况下去除带通和窄带 RFI。脉冲星分别是 J2112+4059、J2113+4644、J0659+1414和J2006+4101。脉冲星 J2112+4059、J0659+1414、J2006+4101 存在强干扰信号，而脉冲星 J2113+4644 存在强脉冲星信号和弱干扰信号。

2  PILAE Hyper Parameter Tuning

We select the data of pulsar J2112+4059 to optimize the hyper parameters of our model, and use the S/N of the single pulse to evaluate the performance. The J2112+4059 original data are shown in Figure 2. The horizontal axis is time and the vertical axis is frequency. The pulsar signal is hard to visualize in Figure 2, because of the existence of strong RFI and varying signal baseline (bandpass). Especially in the low-frequency part, pulsar signal due to the raising baseline. To show the pulsar signal after RFI removal, we apply PILAE to the data in Figure 2, we use 400 neurons in the hidden layer, and λ = 0.1 regularization. After RFI mitigation, the pulsar signal is clearly visible in Figure 3. The pulsar signal in Figure 3 is dispersed by interstellar medium, causing low-frequency signals to arrive later than higher-frequency signals. We can remove this dispersion effect through an operation called de-dispersion. We can fold the de-dispersed data by using the period of the pulsar and summed all the frequencies into a folded pulse profile, and we then calculate the S/N of the profile1 . This S/N is an good indicator of the signal strength and we used it to evaluate our model in subsequent analysis.

选取脉冲星 J2112+4059 的数据对模型的超参数进行优化，并利用单脉冲信噪比来评价模型的性能。J2112+4059 的原始数据如图 2 所示。横轴是时间，纵轴是频率。由于存在强 RFI 和变化的信号基线 (带通)，脉冲星信号在图 2 中很难可视化。特别是在低频部分，脉冲星信号由于基线升高。为了显示去除 RFI 后的脉冲星信号，我们对图 2 中的数据进行了 PILAE 处理，隐藏层使用了 400个神经元，并进行了 λ = 0.1 正则化处理。RFI 减弱后，脉冲星信号在图 3 中清晰可见。图 3 中的脉冲星信号被星际介质分散，导致低频信号比高频信号到达晚。我们可以通过一种叫做去色散的操作来消除这种色散效应。我们可以利用脉冲星的周期折叠去分散的数据，并将所有的频率相加成一个折叠的脉冲剖面，然后计算剖面的信噪比。信噪比是信号强度的一个很好的指标，我们在随后的分析中使用它来评估我们的模型。

To optimize the hyper parameters of our model, we perform two experiments to 1. we experiment different levels of regularization with a fixed-number of hidden layer neurons; and 2. we changed the number of neurons in the hidden layer and find the setting that maximize the resulting pulsar S/N.

In the first experiment, we use J2112+4059 pulsar data to test and optimize for the regularization parameters λ. We set the number of hidden layer neurons to 20, and grid searched λ between 0 and 1. The resulting S/N of the pulsar is listed in Table 1. The experimental results show that the different values of λ have very limited impact to the S/N. Therefore, we choose a medium value of 0.5 for λ in our future experiments.

In the second experiment, we use pulsar J2112+4059, J2113+4644, J0659+1414, and J2006+4101 to fine tune the number of neurons in the hidden layer. We set λ = 0.5, and experimented with a range of numbers between 2 and 400 for the hidden-layer neurons, and calculate the resulting S/Ns after RFI mitigation. Figure 4 shows that for strong pulsars like J2112+4059, J2113+4644, J0659+1414, the optimal number of neurons is possibly around 20. The S/N of relatively weak pulsars like J2006+4101 seems to increase slowly with number of neurons. According to this experiment, we choose to use 20 neurons in the hidden layer for later experiments.

为了优化模型的超参数，我们进行了两次实验：

1. 用固定数目的隐层神经元进行了不同程度的正则化实验；

2. 改变隐藏层的神经元数量，并找到了最大化脉冲星 S/N 的设置。

在第一个实验中，我们利用 J2112+4059 脉冲星数据对正则化参数 λ 进行了测试和优化。我们设置隐层神经元的数目为 20，网格搜索 λ 在 0 到 1 之间。脉冲星的信噪比如表 1 所示。实验结果表明，λ 值的不同对信噪比的影响非常有限。因此，我们在以后的实验中选择了 λ 的中间值 0.5。

第二个实验利用脉冲星 J2112+4059、J2113+4644、J0659+1414、J2006+4101 对隐藏层的神经元数量进行微调。我们设置 λ = 0.5，对隐层神经元进行 2 - 400 范围内的实验，并计算 RFI 消除后得到的 S/Ns。从图 4 可以看出，对于 J2112+4059、J2113+4644、J0659+1414 等强脉冲星，最佳的神经元数量可能在 20 个左右。相对较弱的脉冲星，如 J2006+4101，其信噪比似乎随着神经元数量的增加而缓慢增加。根据这个实验，我们选择在后面的实验中使用隐层中的 20 个神经元。

3.  PILAE Model Performance and Robustness

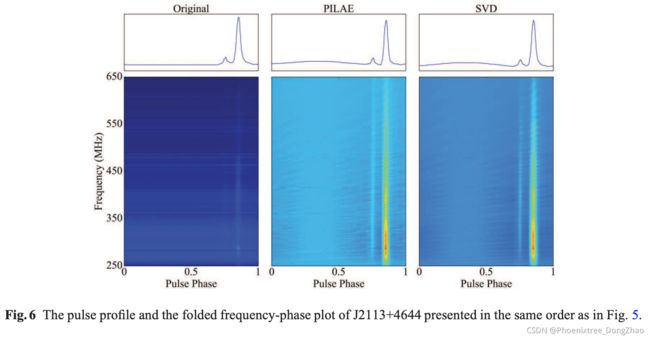
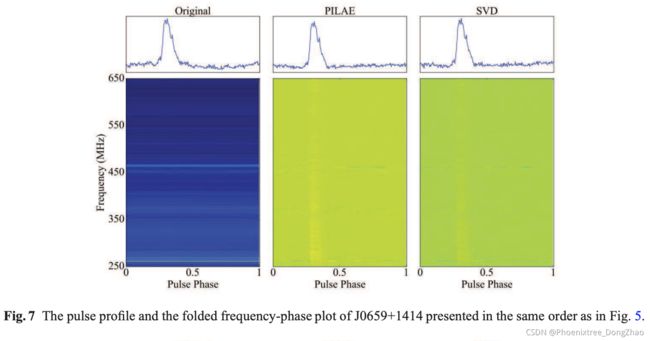
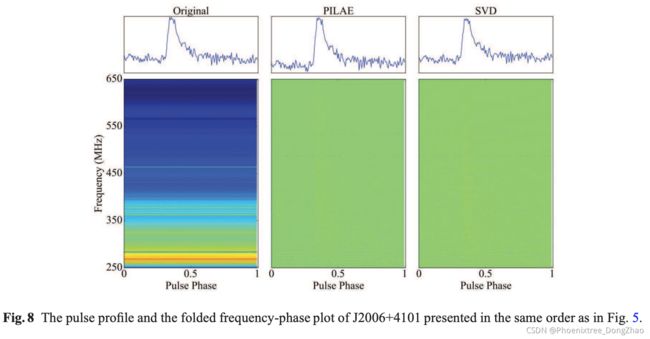
In this section, we use UWB FAST data to test and compare the performance of PILAE and SVD models. We determine the PILAE hyper parameters through the aforementioned experiments and set the number of the hidden layer neurons to 20, and λ to 0.5, and use this model to remove RFI from pulsars J2112+4059, J2113+4644, J0659+1414, and J2006+4101. For the SVD method, we optimize for the best rank of eigenvectors to remove as RFI based on the resulting S/N, and choose 2 of the largest SVD eigenvectors and flagged them as RFI. We present the S/Ns of the pulsar signals before and after applying PILAE and SVD to the data of pulsars J2112+4059, J2113+4644, J0659+1414 and J2006+4101 (Table 2). For PSR J2113+4644, J0659+1414, both models end up improve the S/N of the pulsars. But for PSR J2112+4059, because of the presence of a strong pulsar signal, both PILAE and SVD models seem to have absorbed a small portion of the pulsar signals into its reconstructed RFI and produce reduced S/N. For all four pulsars, the RFI mitigation results of the PILAE method are better than or equal to those of the SVD method. For PSR J2006+4101, we can increase the number of hidden layer neurons in the PIALE method. When the number of hidden layer neurons is set to 200, the S/N of PSR J2006+4101 can reach 25 after RFI removal. We show the pulse profiles and the frequencyphase plot of the four pulsars before and after RFI removal in Figures 5, 6, 7 and 8. The pulse profiles of the strong pulsars J2112+4059 and J2113+4644 show some degree of baseline distortion after RFI treatments, which suggests that PILAE and SVD methods may affect the off pulse profile baseline. The frequency-phase plots of these pulsars show that most of the bright narrow-band RFI features in the original data are no longer visible after the RFI mitigation. However, some weaker narrow-band RFI remains. These remaining RFIs seem to be varying in a short time scale. This suggests that PILAE and SVD-based RFI mitigation methods are best for removing persistent RFIs; while the fast-varying RFIs need to be treated with other techniques.

在本节中使用 UWB FAST 数据来测试和比较 PILAE 和 SVD 模型的性能。通过上述实验确定了 PILAE 超参数，并将隐含层神经元数量设为 20，λ 设为 0.5，利用该模型去除 J2112+4059、J2113+4644、J0659+1414、J2006+4101 脉冲星的 RFI。对于 SVD 方法，根据得到的 S/N 优化出要去除的特征向量的最佳秩为 RFI，并选择 2 个最大的 SVD 特征向量标记为 RFI。本文给出了将 PILAE 和 SVD 应用于脉冲星 J2112+4059、J2113+4644、J0659+1414 和 J2006+4101 数据前后的脉冲星信号的信噪比 (表2)。对于 PSR J2113+4644、J0659+1414，两种模型最终都改善了脉冲星的信噪比。但对于 PSR J2112+4059，由于存在强脉冲星信号，PILAE 和 SVD 模型似乎都吸收了一小部分脉冲星信号到其重建的 RFI 中，导致信噪比降低。对于所有四颗脉冲星，PILAE 方法的 RFI 消除效果均优于或等于 SVD 方法。对于 PSR J2006+4101，可以在 PIALE 方法中增加隐藏层神经元的数量。当隐层神经元数量设置为 200 时，去除 RFI 后 PSR J2006+4101 的信噪比可达 25。在图 5、6、7 和 8 中展示了四颗脉冲星在去除 RFI 前后的脉冲轮廓和频率相位图。强脉冲星 J2112+4059 和 J2113+4644 经过 RFI 处理后的脉冲轮廓出现了一定程度的基线畸变，提示 PILAE 和 SVD 方法可能会对脉冲轮廓基线产生影响。这些脉冲星的频相图显示，大部分原始数据中的明亮窄带 RFI 特征在 RFI 消除后不再可见。然而，一些较弱的窄带射频干扰仍然存在。这些剩余的射频识别似乎在短时间内发生变化。这表明，基于 PILAE 和 SVD 的 RFI 消除方法是去除持久性 RF I的最佳方法；而快速变化的射频识别需要用其他技术来处理。

 

We compared the results of RFI cleaning from the two models and also evaluated the running time of the two methods. FAST pulsar data is a two-dimensional matrix 4096 × 262144. Our method takes a short computing time, it takes ∼0.1 s to remove the RFI from a single set of pulsar data (4096×4096 2D data) using a 24–core computer. A fits data process cost about ∼6 s. SVD method will take about 16 s to finish processing 4096×4096 2D data, it takes ∼17 min to process one fits data. The PILAE method exhibits a faster performance than that exhibited by the SVD method.

本文比较了两种模型的 RFI 消除结果，并对两种方法的运行时间进行了评价。FAST 脉冲星数据是一个二维矩阵 4096 × 262144。本文的方法需要很短的计算时间，使用 24 核计算机从一组脉冲星数据 (4096×4096 2D数据) 中去除 RFI 需要大约 0.1 秒。一个适合的数据处理过程大约需要 6 秒。SVD 方法处理 4096×4096 二维数据需要大约 16 秒，处理一个拟合数据需要大约 17 分钟。PILAE方法比 SVD 方法表现出更快的性能。

Finally, we test whether the randomly initialized PILAE model converges and is robust. The weight of the encoder is randomly initialized to satisfy the Gaussian distribution with mean value 0 and variance 1, the number of hidden layer neurons is set to 20, and the regularization λ is set to 0.5. After removing RFI from J2112+4059 pulsar data, the S/N can be calculated. We perform 10 independent experiments and obtain the mean and standard deviation of the S/N is 62.7(±0.7). In comparison, we use the bootstrap method to estimate the nature random fluctuation in S/N due to sampling. We select one dataset and randomly selected half of its channels to calculate the S/N. The resulting S/N is 58.7(±1.1) in 10 independent experiments. The experimental results show that the error caused by random initialization of the encoder weight is comparable to the nature fluctuation of S/N itself and does not cause substantial extra divergence, indicating that the performance of the PILAE model is robust against random initialization.

最后，测试了随机初始化的 PILAE 模型是否收敛和鲁棒性。对编码器的权值进行随机初始化，使其满足均值为 0、方差为 1 的高斯分布，设隐层神经元数为 20，正则化 λ 设为 0.5。在去除J2112+4059 脉冲星数据的 RFI 后，计算其信噪比。10 次独立实验，得到 S/N 的均值和标准差为62.7(±0.7)。相比之下，使用 bootstrap 方法来估计由于抽样而导致的信噪比的自然随机波动。我们选取一个数据集，随机选取其中一半的信道计算信噪比。10 次独立实验的信噪比为 58.7(±1.1)。实验结果表明，编码器权值的随机初始化所产生的误差与信噪比本身的自然波动相当，不会产生很大的额外发散，说明 PILAE 模型对随机初始化具有较强的鲁棒性。

Discussion and Conclusions 

In this paper, we introduce a new RFI mitigation algorithm – PILAE. This algorithm can remove both persistent narrow-band RFI and the bandpass from pulsar data. Traditional threshold-based filter method often completely removes all data in bad channels or contaminated spectral samples, causes the pulsar signals in those channels and samples to be lost. We demonstrate in Section 3 Table 2 that PILAE could cleanly remove both types of RFI yet retain majority of the pulsar signals. This is a highly desirable feature for pulsar searching as well as for a slew of other exploratory scientific objectives (Li et al. 2019) including radio exoplanets, gravitational wave, and so on. We also demonstrate that our method is slightly better than the state-of-the-art SVD-based RFI removal technique in recovering pulsar signals (Table 2), as well as taking less computing cycles to complete (Sect. 3.3). Although better than threshold-based method in principle, the PILAE method and the SVD method share the same caveat that they sometimes still remove a small potion of the pulsar signal, especially when the pulsar is substantially stronger than the RFIs. In these cases (for example for PSR J2122+4059), the PILAE and SVD methods still could clearly enhance the visibility of the signal to eyes, and they are unlikely to hinder the detection of the pulsar signal because they are already very strong. However, it is not advised to use these methods to precisely measure the pulse profiles and polarizations because they could introduce small distortion to the baseline.

本文介绍了一种新的 RFI 抑制算法—— PILAE。该算法可以去除脉冲星数据中持续的窄带 RFI 和带通。传统的基于阈值的滤波方法往往将坏通道或污染光谱样本中的所有数据完全去除，导致这些通道和样本中的脉冲星信号丢失。本文证明，PILAE 可以清晰地去除两种类型的 RFI，同时保留大部分脉冲星信号。这是脉冲星搜索以及一系列其他探索科学目标 (Li et al. 2019) 的一个非常理想的特征，包括射电系外行星、引力波等。本文还证明，在恢复脉冲星信号方面，我们的方法比最先进的基于 SVD 的 RFI 去除技术略好，并且需要更少的计算周期。

尽管 PILAE 方法和 SVD 方法在原理上优于基于阈值的方法，但它们有一个共同的缺点，那就是它们有时仍然会去除一小部分脉冲星信号，特别是当脉冲星明显强于 RFI 时。在这些情况下 (例如PSR J2122+4059)， PILAE 和 SVD 方法仍然可以清晰地增强信号对人眼的可见性，而且它们不太可能阻碍脉冲星信号的探测，因为它们已经非常强了。然而，不建议使用这些方法来精确测量脉冲轮廓和极化，因为它们可能会对基线造成小的失真。

At present, FAST produces over two hundred terabytes of data per day. During one night of drift-scan, the telescope produces around 10 000 fits files in pulsar search project. Therefore, we need an efficient way to process data in order to keep up with the data stream. The training of PIL is easier than other deep-learning methods because the training process does not require back-propagation. It takes ∼6 s to process one fits data using a 24–core computer without considering I/O time. We can process ∼ 14 000 fits data per day using this method. Therefore, this method can be implemented efficiently and it can meet the requirements of real-time processing of FAST data.

目前，FAST 每天产生超过 200tb 的数据。在一个晚上的漂移扫描中，该望远镜在脉冲星搜索项目中产生了大约 10,000 个适合文件。因此，我们需要一种有效的方法来处理数据，以跟上数据流。PIL 的训练比其他深度学习方法更容易，因为训练过程不需要反向传播。如果不考虑 I/O 时间，用24 核计算机处理一个适合的数据需要大约 6 秒。使用这种方法，我们每天可以处理约 14000 个拟合数据。因此，该方法能够有效地实现，能够满足 FAST 数据实时处理的要求。

We could use this method to quickly clean the data and then process the results by eye or other searching techniques to determine whether or not they contain pulsar signals. In the future, machine learning methods can be used to identify these images directly, which will greatly improve the efficiency of the pulsar search.

我们可以使用这种方法快速清理数据，然后通过眼睛或其他搜索技术处理结果，以确定它们是否包含脉冲星信号。在未来，可以使用机器学习方法直接识别这些图像，这将大大提高脉冲星搜索的效率。

In this work, we find the optimal hyper parameters through grid search. In future work, the hyper parameters could be determined automatically through the method of auto machine leaning (Yao et al. 2018).

在本文中，我们通过网格搜索来寻找最优超参数。在未来的工作中，可以通过自动机器学习的方法自动确定超参数 (Yao et al. 2018)。