leetcode刷题01：二叉树的前序、中序、后序、层次遍历（python实现）

二叉树的前序、中序、后序、层次遍历

本文主要汇总leetcode中涉及到二叉树前、中、后、层次遍历的题目以及对应的思路和解答。

关于普通的前后中层次遍历：

目前我整理的有递归和迭代两种实现方式（前中后遍历）

递归和迭代两种思路都有套路可言，比如递归实现只需要改变一下代码的位置，而迭代涉及到栈的使用，层次遍历主要用到队列

144：二叉树的前序遍历

前序遍历节点顺序为中、左、右即父节点、左子树、右子树

递归实现

其实我之前对前序遍历的递归实现也比较晕，在看了大话数据结构之后，里面讲解的递归实现我感觉比较通俗易懂，理解了之后就知道递归的代码很有套路可言。

思路：

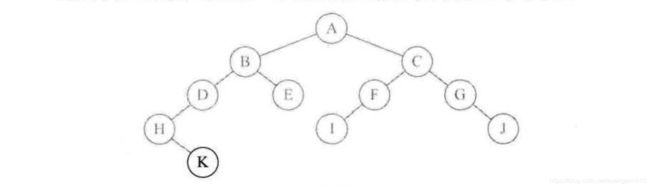
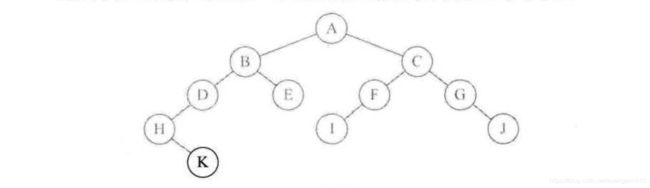
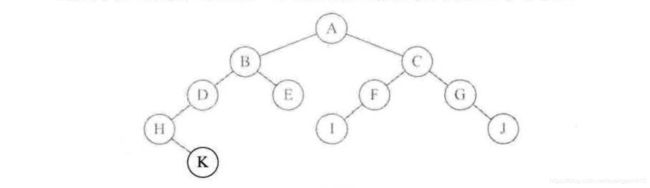
如上树的前序遍历的结果是ABDHKECFIGJ.

1、首先从节点A开始，存储A的值，遍历A的左子树B

2、由于B不为空，所以存储B的值，继续遍历B的左子树D

3、D不为空，存储D的值，遍历D的左子树H

4、H不为空，存储H的值，遍历H的左子树

5、H的左子树为空，返回到上层递归，即对应的4操作，接着遍历H的右子树K

6、K不为空，存储K的值，遍历K的左子树

7、K的左子树为空，返回到6，遍历K的右子树

8、K的右子树为空，返回到3，遍历D的右子树

9、……以此类推

代码实现：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.result = []
    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        
        self.result.append(root.val)
        self.preorderTraversal(root.left)
        self.preorderTraversal(root.right)
        return self.result

迭代实现

前序遍历的迭代遍历用到了栈, 遵循先进后出，所以先存右子树的值，再存左子树的值

入栈顺序中右左，出栈顺序中左右，即前序顺序中左右

思路：

1、定义栈stack以及存放最终结果的result，先把父节点A存进stack，stack = [A]

2、取出stack中的A，stack=[]，将A的值存入result，由于先进后出，所以将A的右子树C存入stack，再存入A的左子树B，此时stack=[C,B]

3、stack不为空，B出栈，stack=[C]，将B的值存入result，result=[A,B],遍历B的左右子树，将右、左子树分别存入stack, 此时stack=[C,E,D]

4、stack不为空，D出栈，stack=[C,E], 将D的值存入result, result=[A,B,D]，遍历D的左右子树，由于D只有左子树，所以stack入栈H，stack=[C,E,H]

5、stack不为空，H出栈, stack=[C,E]，将H的值存储result，result=[A,B,D,H]，遍历H的左右子树，H只有右子树，stack入栈K，stack=[C,E,K]

6、stack不为空，K出栈，stack=[C,E]，将K的值存入result, result=[A,B,D,H,K]，遍历K的左右子树，为空，不入栈

7、stack不为空，E出栈, stack=[C], 将E的值存入result，result=[A,B,D,H,K,E]，遍历E的左右子树,为空，不入栈

8、stack不为空，C出栈，stack=[ ], 将C的值存入result，result=[A,B,D,H,K,E,C]，遍历C的左右子树，有左右子树，分别入栈G，F, 此时stack=[G,F]

9、……以此类推

代码实现：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):

    def preorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        
        stack = [root]
        result = []
        while stack:
            data = stack.pop()
            result.append(data.val)
            if data.right:
                stack.append(data.right)
            if data.left:
                stack.append(data.left)
        return result

94：二叉树的中序遍历

中序遍历的顺序为左、中、右，即左子树、父节点、右子树

递归实现

1、从A节点开始遍历，遍历A的左子树B

2、B不为空、遍历B的左子树D

3、D不为空，遍历D的左子树H

4、H不为空，遍历H的左子树

5、H的左子树为空，回退到上层遍历4

6、存储H的值，遍历H的右子树K

7、K的左子树为空，回退到6，存储K的值，遍历K的右子树

8、K的左右子树均为空，回退6，H的左右子树均遍历完，回退3，遍历D的右子树

9、D的右子树为空，回退到2，遍历B的右子树

10、……以此类推

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.result = []
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []

        self.inorderTraversal(root.left)
        self.result.append(root.val)
        self.inorderTraversal(root.right)
        return self.result

迭代实现

中序遍历的迭代也是使用栈，利用栈的先进后出

入栈顺序左右中，出栈顺序左中右，即中序顺序左中右

1、stack入栈根节点A，stack=[A]，遍历A的左子树B

2、B不为空，入栈B，stack=[A,B]，遍历B的左子树D

3、D不为空，入栈D，stack=[A,B,D]，遍历D的左子树H

4、H不为空，入栈H，stack=[A,B,D,H]，遍历H的左子树

5、H的左子树为空，stack出栈H，stack=[A,B,D], result存储H的值，result=[H]，遍历H的右子树K

6、K不为空，入栈K，stack=[A,B,D,K], 遍历K的左子树

7、K的左子树为空，stack出栈K，stack=[A,B,D], result=[H,K]，接着遍历K的右子树

8、K的右子树为空，出栈D, stack=[A,B], 存储D的值，result=[H,K,D]，遍历D的右子树

9、D的右子树为空，出栈B, stack=[A], 存储B的值，result=[H,K,D,B]，遍历B的右子树E

10、……以此类推

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):

    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []

        stack, result = [], []
        while stack or root:
            if root:
                stack.append(root)
                root = root.left
            else:
                data = stack.pop()
                result.append(data.val)
                root = data.right
        return result

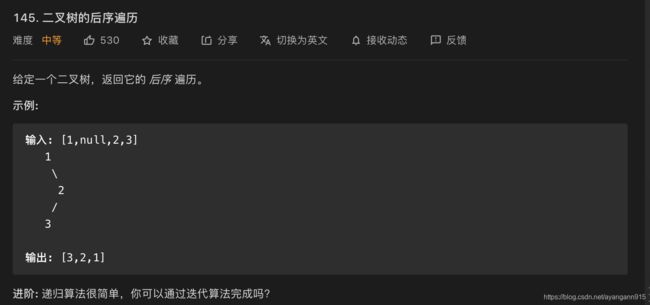
145：二叉树的后序遍历

后序遍历的顺序为左右中，即左子树，右子树，父节点

递归实现

1、遍历A的左子树B

2、遍历B，B不为空、遍历B的左子树D

3、遍历D，D不为空，遍历D的左子树H

4、遍历H，H不为空，遍历H的左子树

5、H的左子树为空，回退到4，遍历H的右子树K

6、遍历K，K不为空，遍历K的左子树

7、K的左子树为空，回退到6，遍历K的右子树

8、K的右子树为空，回退到6，存储K的值，result=[K]

9、回退到4，H的左右子树均遍历完，存储H的值，result=[K,H]

10、回退到3，遍历D的右子树

11、D的右子树为空，回退到3，存储D的值，result=[K,H,D]

12、D遍历完，回退到2，遍历B的右子树E

13、……以此类推

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.result = []

    def postorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        # 递归写法
        if not root:
            return []
    
        self.postorderTraversal(root.left)
        self.postorderTraversal(root.right)
        self.result.append(root.val)
        return self.result

迭代实现

后序遍历的迭代实现和前序遍历有些类似，最后做了一个倒序

代码中入栈顺序是中左右，出栈顺序是中右左，倒序之后是左右中，即后序顺序

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):

    def postorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        if not root:
            return []
        
        stack, result = [root], []
        while stack:
            root = stack.pop()
            result.append(root.val)
            if root.left:
                stack.append(root.left)
            if root.right:
                stack.append(root.right)
        return result[::-1]

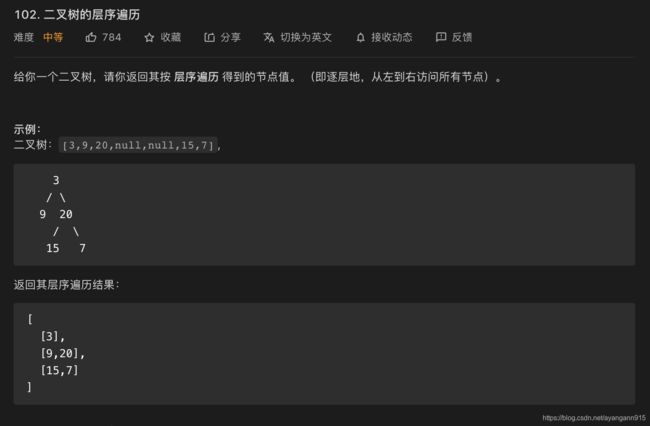
102：二叉树的层序遍历

层序遍历即广度优先，按照从上到下，从左到右的顺序依次取值

层序遍历主要用到了队列，利用其先进先出，同时要保证每一行的数据在一个列表之中

1、队列queue中先存储根节点A的值，queue=[A], result=[]，使用临时列表存储每一行的值

2、queue不为空，队列出值A，temp=[A], result=[[A]], 判断A的左右子树，左子树B，右子树C，分别入队列queue，queue=[B,C]

3、此时队列长度为2，循环两次，分别获取队列中值对应的左右子树值，然后将其入队

4、循环第一次，B出队列，temp=[B], B的左右子树进队列，queue=[C,D,E]

5、循环第二次，C出队列，temp=[B,C]，C的左右子树进队列，queue[D,E,F,G]

6、循环两次之后，result=[[A],[B,C]], temp=[],此时queue的长度为4，接下来再次循环四次

7、……以此类推

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def levelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []

        queue = [root]
        result = []
        while queue:
            temp = []
            size = len(queue)
            for i in range(size):
                data = queue.pop(0)
                temp.append(data.val)
                if data.left:
                    queue.append(data.left)
                if data.right:
                    queue.append(data.right)
            result.append(temp)
        return result

107：二叉树的层次遍历II

这道题和102题目差不多，每次将值插入到index=0的位置即可

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def levelOrderBottom(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        
        queue, res = [root], []
        while queue:
            size = len(queue)
            temp = []
            for i in range(size):
                root = queue.pop(0)
                if root:    
                    temp.append(root.val)
                if root.left:
                   queue.append(root.left)
                if root.right:
                    queue.append(root.right) 
            res.insert(0, temp)
        return res

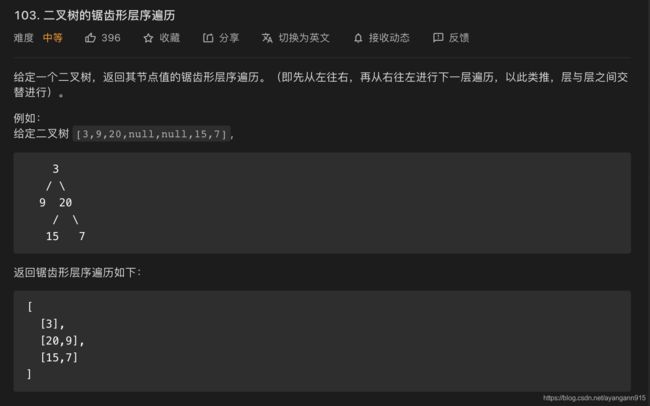
103. 二叉树的锯齿形层序遍历

由测试用例可知，单层从左到右，双层从右到左。

锯齿形层序遍历和层序遍历的逻辑都差不多，只不过在往临时列表中存储数据时，需要考虑将其存在什么位置。

使用is_odd来判断是单层还是双层，第一层是单层

1、第一层是单层，queue=[A], size=1,循环一次, result=[]

2、temp=[], 第一次循环，队列出A，单层，temp=[A]，A 的右子树为C，左子树为B，入队列queue=[C,B], result=[[A]], is_odd=False，循环完毕

3、第二层是双层，is_odd=False, queue=[C,B],size=2,循环2次

4、第一次循环，出队列C，temp=[C], C 的右左子树为G，F，queue=[B,G,F]

5、第二次循环，出队列B，双层append，temp=[C,B], queue=[G,F,E,D]，result=[[A],[C,B]], is_odd=False

6、第三层，is_odd=False, queue=[G,F,E,D]，size=4, 循环4次

7、第一次循环，出队列G，temp=[G], 右子树J，queue=[F,E,D,J]

8、第二次循环，出队列F, 单层insert, temp=[F,G], 左子树I，queue=[E,D,J,I]

9、第三次循环，出队列E，单层insert，temp=[E,F,G], queue=[D,J,I]

10、第四次循环，出队列D，单层insert，temp=[H,E,F,G],queue=[J,I]

11、……以此类推

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def zigzagLevelOrder(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        if not root:
            return []
        
        queue, result = [root], []
        is_odd = True
        while queue:
            size = len(queue)
            temp = []
            for i in range(size):
                root = queue.pop(0)
                if is_odd:
                    temp.insert(0, root.val)
                if not is_odd:
                    temp.append(root.val)
                if root.right:
                    queue.append(root.right)
                if root.left:
                    queue.append(root.left)

            is_odd = not is_odd
            result.append(temp)
        return result