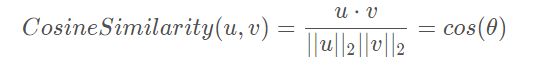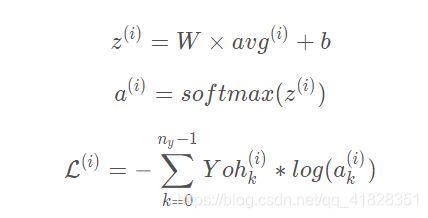词向量的运算与Emoji生成器
本文参考参考,没有对框架内容进行学习,旨在学习思路和方法。
1、词向量运算
之前学习RNN和LSTM的时候,输入的语句都是一个向量,比如恐龙的名字那个例子就是将一个单词中的字母按顺序依次输入,这对于一个单词的预测是可行的。但是对于想让机器学习到一个句子的意思那就不行了,它需要知道每个单词的意思,而且还需要知道单词连起来的意思,这时候输入到网络中的单位就不是字母了,应该是按单词来输入。这时候问题就来了,单词该如何输入到网络之中。有人将很多单词训练成为了词嵌入数据,每个单词对应一个50维的向量。
使用别人造好的轮子载入:可以看到单词hello对应的词向量。word_to_vec_map是单词到词向量的映射字典
words, word_to_vec_map = w2v_utils.read_glove_vecs('data/glove.6B.50d.txt')
print(word_to_vec_map['hello'])
"""
[-0.38497 0.80092 0.064106 -0.28355 -0.026759 -0.34532 -0.64253
-0.11729 -0.33257 0.55243 -0.087813 0.9035 0.47102 0.56657
0.6985 -0.35229 -0.86542 0.90573 0.03576 -0.071705 -0.12327
0.54923 0.47005 0.35572 1.2611 -0.67581 -0.94983 0.68666
0.3871 -1.3492 0.63512 0.46416 -0.48814 0.83827 -0.9246
-0.33722 0.53741 -1.0616 -0.081403 -0.67111 0.30923 -0.3923
-0.55002 -0.68827 0.58049 -0.11626 0.013139 -0.57654 0.048833
0.67204 ]
"""那该如何去对比两个单词的近似程度呢?这里就引入了余弦相似度。越相似,余弦值越接近1,否则越接近0
def cosine_similarity(u, v):
"""
u与v的余弦相似度反映了u与v的相似程度
参数:
u -- 维度为(n,)的词向量
v -- 维度为(n,)的词向量
返回:
cosine_similarity -- 由上面公式定义的u和v之间的余弦相似度。
"""
distance = 0
# 计算u与v的内积
dot = np.dot(u, v)
#计算u的L2范数
norm_u = np.sqrt(np.sum(np.power(u, 2)))
#计算v的L2范数
norm_v = np.sqrt(np.sum(np.power(v, 2)))
# 根据公式1计算余弦相似度
cosine_similarity = np.divide(dot, norm_u * norm_v)
return cosine_similarity
father = word_to_vec_map["father"]
mother = word_to_vec_map["mother"]
ball = word_to_vec_map["ball"]
crocodile = word_to_vec_map["crocodile"]
france = word_to_vec_map["france"]
italy = word_to_vec_map["italy"]
paris = word_to_vec_map["paris"]
rome = word_to_vec_map["rome"]
print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother))
print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile))
print("cosine_similarity(france - paris, rome - italy) = ",cosine_similarity(france - paris, rome - italy))
"""
cosine_similarity(father, mother) = 0.8909038442893615
cosine_similarity(ball, crocodile) = 0.27439246261379424
cosine_similarity(france - paris, rome - italy) = -0.6751479308174202
"""上面是两个词之间的相似程度计算,那词类类比该如何计算。 形如A与B相比就类似于C与____相比一样,这里计算的就是差值之间的余弦相似度。这种类比需要去遍历词库来寻找最大的相似度。
def complete_analogy(word_a, word_b, word_c,word_to_vec_map):
# 把单词转换为小写
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
# 获取对应单词的词向量
e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b], word_to_vec_map[word_c]
# 获取全部的单词
words = word_to_vec_map.keys()
# 将max_cosine_sim初始化为一个比较大的负数
max_cosine_sim = -100
best_word = None
# 遍历整个数据集
for word in words:
# 要避免匹配到输入的数据
if word in [word_a, word_b, word_c]:
continue
# 计算余弦相似度
cosine_sim = cosine_similarity((e_b - e_a), (word_to_vec_map[word] - e_c))
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = word
return best_wordtriads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} <====> {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))
"""
italy -> italian <====> spain -> spanish
india -> delhi <====> japan -> tokyo
man -> woman <====> boy -> girl
small -> smaller <====> large -> larger
"""消除与性别无关的词汇的偏差:有很多词是与性别没有关系的比如reception,但是在实际的比较中却给予了相关性,这就要求消除这种偏差。做法就是将需要计算的词向量向相关轴投影,然后减去该投影就消除了偏差
def neutralize(word, g, word_to_vec_map):
"""
通过将“word”投影到与偏置轴正交的空间上,消除了“word”的偏差。
该函数确保“word”在性别的子空间中的值为0
参数:
word -- 待消除偏差的字符串
g -- 维度为(50,),对应于偏置轴(如性别)
word_to_vec_map -- 字典类型,单词到GloVe向量的映射
返回:
e_debiased -- 消除了偏差的向量。
"""
# 根据word选择对应的词向量
e = word_to_vec_map[word]
# 根据公式2计算e_biascomponent
e_biascomponent = np.divide(np.dot(e, g), np.square(np.linalg.norm(g))) * g
# 根据公式3计算e_debiased
e_debiased = e - e_biascomponent
return e_debiased
e = "receptionist"
print("去偏差前{0}与g的余弦相似度为:{1}".format(e, cosine_similarity(word_to_vec_map["receptionist"], g)))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("去偏差后{0}与g的余弦相似度为:{1}".format(e, cosine_similarity(e_debiased, g)))
"""
e = "receptionist"
print("去偏差前{0}与g的余弦相似度为:{1}".format(e, cosine_similarity(word_to_vec_map["receptionist"], g)))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("去偏差后{0}与g的余弦相似度为:{1}".format(e, cosine_similarity(e_debiased, g)))
"""
2、 表情生成器
所谓表情生成器就是根据我们输入的语句来生成相对应的表情。比如:“Congratulations on the promotion! ? Lets get coffee and talk. ☕️ Love you! ❤️”。
练习中构建的一个简单的分类器,数据集(X,Y),X是127条字符串类型的短句子,Y是对应的(0-4)5个标签。测试集总共有56条数据。
X_train, Y_train = emo_utils.read_csv('data/train_emoji.csv')
X_test, Y_test = emo_utils.read_csv('data/test.csv')
maxLen = len(max(X_train, key=len).split())
index = 3
print(X_train[index], emo_utils.label_to_emoji(Y_train[index]))
"""
Miss you so much ❤️
"""在模型上输入是将所有的单词的向量相加求均值然后作为输入输入到模型当中,然后将输入和权重相乘激活。
def sentence_to_avg(sentence, word_to_vec_map):
"""
将句子转换为单词列表,提取其GloVe向量,然后将其平均。
参数:
sentence -- 字符串类型,从X中获取的样本。
word_to_vec_map -- 字典类型,单词映射到50维的向量的字典
返回:
avg -- 对句子的均值编码,维度为(50,)
"""
# 第一步:分割句子,转换为列表。
words = sentence.lower().split()
# 初始化均值词向量
avg = np.zeros(50,)
# 第二步:对词向量取平均。
for w in words:
avg += word_to_vec_map[w]
avg = np.divide(avg, len(words))
return avg
要注意和权重相乘时是求的内积,所以维度会不匹配。
def model(X, Y, word_to_vec_map, learning_rate=0.01, num_iterations=400):
"""
在numpy中训练词向量模型。
参数:
X -- 输入的字符串类型的数据,维度为(m, 1)。
Y -- 对应的标签,0-7的数组,维度为(m, 1)。
word_to_vec_map -- 字典类型的单词到50维词向量的映射。
learning_rate -- 学习率.
num_iterations -- 迭代次数。
返回:
pred -- 预测的向量,维度为(m, 1)。
W -- 权重参数,维度为(n_y, n_h)。
b -- 偏置参数,维度为(n_y,)
"""
np.random.seed(1)
# 定义训练数量
m = Y.shape[0]
n_y = 5
n_h = 50
# 使用Xavier初始化参数
W = np.random.randn(n_y, n_h) / np.sqrt(n_h)
b = np.zeros((n_y,))
# 将Y转换成独热编码
Y_oh = emo_utils.convert_to_one_hot(Y, C=n_y)
# 优化循环
for t in range(num_iterations):
for i in range(m):
# 获取第i个训练样本的均值
avg = sentence_to_avg(X[i], word_to_vec_map)
# 前向传播
z = np.dot(W, avg) + b
a = emo_utils.softmax(z)
# 计算第i个训练的损失
cost = -np.sum(Y_oh[i]*np.log(a))
# 计算梯度
dz = a - Y_oh[i]
dW = np.dot(dz.reshape(n_y,1), avg.reshape(1, n_h))
db = dz
# 更新参数
W = W - learning_rate * dW
b = b - learning_rate * db
if t % 100 == 0:
print("第{t}轮,损失为{cost}".format(t=t,cost=cost))
pred = emo_utils.predict(X, Y, W, b, word_to_vec_map)
return pred, W, b
pred, W, b = model(X_train, Y_train, word_to_vec_map)
"""
第0轮,损失为1.9520498812810072
Accuracy: 0.3484848484848485
第100轮,损失为0.07971818726014807
Accuracy: 0.9318181818181818
第200轮,损失为0.04456369243681402
Accuracy: 0.9545454545454546
第300轮,损失为0.03432267378786059
Accuracy: 0.9696969696969697
"""X_my_sentences = np.array(["i adore you", "i love you", "funny lol", "lets play with a ball", "food is ready", "you are not happy"])
Y_my_labels = np.array([[0], [0], [2], [1], [4],[3]])
pred = emo_utils.predict(X_my_sentences, Y_my_labels , W, b, word_to_vec_map)
emo_utils.print_predictions(X_my_sentences, pred)
"""
Accuracy: 0.8333333333333334
i adore you ❤️
i love you ❤️
funny lol ?
lets play with a ball ⚾
food is ready ?
you are not happy ❤️
"""LSTM下的表情生成
可以看到上文中的最后一个结果预测是不正确的,这是因为没有做一个上下文的考虑 。对应上面的预测方法,这里是将单词转化成向量矩阵作为序列输入。这里的输入长度是固定的,设定一个最大长度,不足的补0,超过的截取。
def sentences_to_indices(X, word_to_index, max_len):
"""
输入的是X(字符串类型的句子的数组),再转化为对应的句子列表,
输出的是能够让Embedding()函数接受的列表或矩阵(参见图4)。
参数:
X -- 句子数组,维度为(m, 1)
word_to_index -- 字典类型的单词到索引的映射
max_len -- 最大句子的长度,数据集中所有的句子的长度都不会超过它。
返回:
X_indices -- 对应于X中的单词索引数组,维度为(m, max_len)
"""
m = X.shape[0] # 训练集数量
# 使用0初始化X_indices
X_indices = np.zeros((m, max_len))
for i in range(m):
# 将第i个居住转化为小写并按单词分开。
sentences_words = X[i].lower().split()
# 初始化j为0
j = 0
# 遍历这个单词列表
for w in sentences_words:
# 将X_indices的第(i, j)号元素为对应的单词索引
X_indices[i, j] = word_to_index[w]
j += 1
return X_indices
X1 = np.array(["funny lol", "lets play baseball", "food is ready for you"])
X1_indices = sentences_to_indices(X1,word_to_index, max_len = 5)
print("X1 =", X1)
print("X1_indices =", X1_indices)
"""
X1 = ['funny lol' 'lets play baseball' 'food is ready for you']
X1_indices = [[155345. 225122. 0. 0. 0.]
[220930. 286375. 69714. 0. 0.]
[151204. 192973. 302254. 151349. 394475.]]
"""