matlab 沙丁,基于三维空间关于海豚围捕沙丁鱼群的运动规律
1. 引言
1.1. 问题的产生
沙丁鱼以聚成大群的方式来对抗海豚的捕食。由于水下光线很暗,所以在距离较远时,海豚只能使用回声定位方法来判断鱼群的整体位置,难以分辨每个个体。鱼群的行动是有协调性的,在没有外部威胁或障碍物时,鱼群常常会聚成接近球形的形态。而当海豚接触甚至冲进鱼群,鱼群则会进行协同的躲避,所以不易在大鱼群中追踪一个目标。沙丁鱼的这种群体行为降低了其被海豚捕食的概率。
问题一:建立合理的数学模型来描述沙丁鱼群在遇到一条海豚捕食时的运动规律。
问题二:智商较高的海豚会配合行动,以图提高捕食的效率。建立合理的数学模型,研究多条海豚配合捕食时应当采取怎样的合作策略。
2. 问题的分析
2.1. 分析集群中单个鱼游动的特点进行
根据集群的四个运动原则:避免碰撞,速度匹配,中心聚集,惯性因素,并参考程淑红 [1] 等人的基于视觉感知的鱼群运动行为特征模型,对各个方向求取加权,建立个体运动方向的数据模型由此可对每一条鱼的运动状态进行迭代更新。
这四个方向的平均方向作为鱼下一时刻游动的方向。即为下一时刻该鱼的游动方向。用公式表示为:
![]()
其中,
λ
1
+
λ
2
+
λ
3
+
λ
4
=
1 。
由此可以从单条鱼拓展到整个沙丁鱼群,进而分析整个鱼群的运动。
2.2. 分析海豚群体与沙丁鱼群体的速度特点
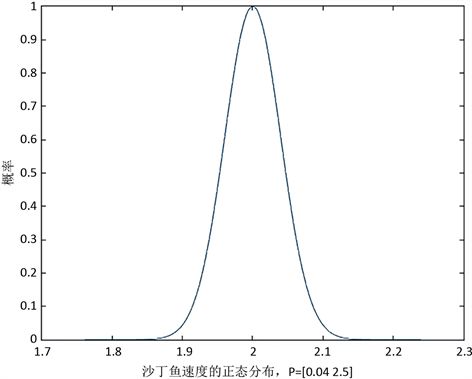
参考周应祺 [2] 等人的鱼类集群行为的研究,我们假设海豚群体的最大速度相同,且符合均值μ为2.5,方差σ为0.04的正态分布,如图1。同时我们假设沙丁鱼群体的最大速度相同,且符合均值μ为2,方差σ为0.04的正态分布,如图2。且海豚群体和沙丁鱼群体各个方向分速度之和不能超过本身速度最大值,如果大于本身速度最大值,则方向取分速度和的方向,大小取速度最大值。
类比于人类平常走路和发生紧急情况时奔跑的关系,假设沙丁鱼最大速度为
v
s
max ,平时速度为
0.3
v
s
max ,躲避同伴拥挤时速度为
0.3
v
s
max ,躲避海豚时速度为
v
s
max 。假设海豚最大速度为
v
h
max ,海豚靠近沙丁鱼时速度为
0.3
v
h
max ,围捕沙丁鱼时速度为
v
h
max 。
2.3. 合理运用粒子群优化算法来表示海豚个体与沙丁鱼群的运动变化, 多只海豚相互配合捕食沙丁鱼的运动情况,并用MATLAB进行仿真检测
粒子群优化(PSO)算法是Kennedy和Eberhart受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。
生物学家Craig Reynolds在1987年提出了一个非常有影响的鸟群聚集模型,在他的仿真中,每一个个体遵循:
Figure 1. Normal distribution of sardine speed
图1. 沙丁鱼速度的正态分布
Figure 2. Normal distribution of dolphin velocity
图2. 海豚速度的正态分布
1) 避免与邻域个体相冲撞;
2) 匹配邻域个体的速度;
3) 飞向鸟群中心,且整个群体飞向目标。
仿真中仅利用上面三条简单的规则,就可以非常接近的模拟出鸟群飞行的现象。
PSO初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己;第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
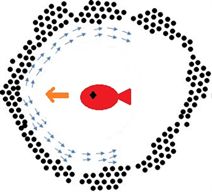
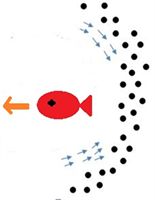
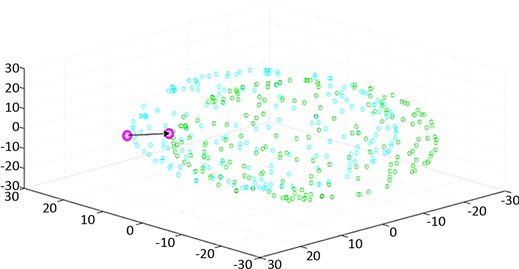
Figure 3. Schematic diagram of the effects of individual dolphins on fish movement: (black spots are sardines)
图3. 海豚个体对鱼群运动影响示意图:(黑点为沙丁鱼)
如图3(a)所示,海豚刚开始被沙丁鱼群感知时,在鱼群前方的鱼感知到危险后开始后退,并向周围发出告警信号。
如图3(b)所示,海豚进入到鱼群中后,沙丁鱼开始整体向远离海豚的方向运动,原来位于前方的鱼大部分撤离到安全区域,绕到了海豚后方的位置,并仍未与鱼群脱离。
如图3(c)所示,海豚离开沙丁鱼群后,鱼群会聚拢,再次形成一个同一整体,并整体向远离海豚的方向运动。
通过这种思路,我们可以简单地模拟出多只海豚配合捕捉沙丁鱼的集群运动。
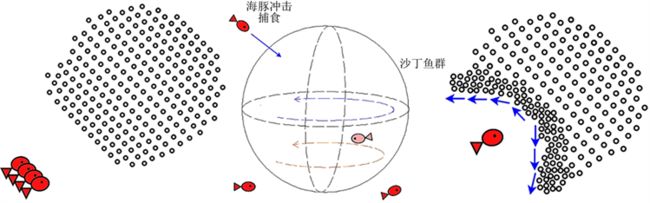
如图4(a)所示,海豚声波定位发现沙丁鱼群,并以最大速度向鱼群运动,直到声波定位失效,开始以自身侧线在一定范围的感知作用内感知到沙丁鱼。
如图4(b)所示,一条海豚在沙丁鱼群上部,防止沙丁鱼从上部逃散,使沙丁鱼群逐渐聚拢,并将沙丁鱼群聚拢到一定程度后冲进鱼群捕食。剩下的海豚在沙丁鱼群下方防止沙丁鱼群逃向海底,并逐渐使沙丁鱼群向中心靠拢。
如图4(c)所示,为沙丁鱼群上部海豚冲进鱼群捕食的俯视图。
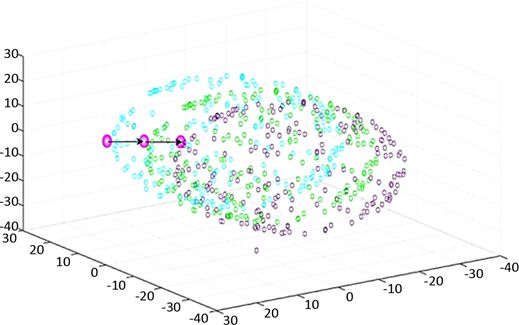
Figure 4. Schematic diagram of the effect of interacting dolphins on fish movement: (black spots are sardines)
图4. 相互配合的海豚对鱼群运动影响示意图:(黑点为沙丁鱼)
海豚种群捕捉沙丁鱼种群时十分讲究排兵布阵,兵分几路,一部分摆出一个口袋型的包围圈,一部分海豚充当“轰赶者”,将猎物向包围圈中驱赶,防止沙丁鱼扩散逃跑。
3. 模型的建立和求解
3.1. 沙丁鱼运动规则
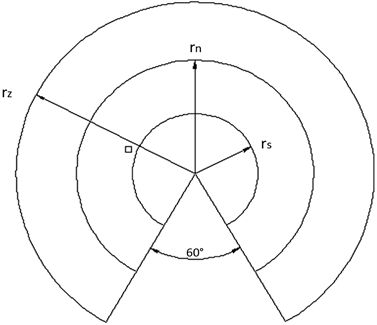
根据鱼体能力范围r的划分来定义鱼体反应方式。根据所查阅资料发现在一些个体数量不多、密度不是很高的群体中,少量个体的游泳方向呈现随机性。在模型中将鱼体视觉能力范围r划分为三个距离,如图5所示。其中
r
s 为单独距离。按避免碰撞原则,邻居鱼j处于本鱼i的排斥区域内,本鱼i将以背离邻居鱼j方向迅速离开;
r
n
−
r
s 为无反应的邻居距离,邻居鱼j处于本鱼i的无反应邻居区域内,本鱼i将以群体平均速度前进,并且在方向上具有较大的随机性;
r
z
−
r
n 为本鱼i的排外距离,当海豚处于该距离内时,本鱼i按照“躲避威胁”的原则会选择逃离并传递危险信号给邻居鱼j。距离
r
z 之外不属于个体的感知范围。
Figure 5. Schematic diagram of the range of fish visual capabilities
图5. 鱼类视觉能力范围示意图
首先要得出单个沙丁鱼的游动方向。为了形象地描述其游动规律,经过查阅资料和观察视频,我们抽象出鱼类产生集群运动的五个游动规则:
1) 避免碰撞:避免和相邻个体发生碰撞,当相邻个体进入独立区域时,该沙丁鱼回向相反方向避让。
2) 速度匹配:匹配邻域个体的速度,与整个群体运动的速度几乎一致。
3) 中心聚集:系统中所有个体向中心聚集。
4) 惯性因素:因为个体鱼的游动惯性而对下一周期的运动方向产生的影响。
5) 威胁源:当海豚靠近沙丁鱼,出现在沙丁鱼感知的排外区域范围内时,沙丁鱼将产生避险意识,避险方向为海豚到沙丁鱼的方向。
因此,本文把这五个方向的平均方向作为鱼下一时刻游动的方向。即为下一时刻该鱼的游动方向。用公式表示为:
V
t
+
1
=
V
1
t
+
V
2
t
+
V
3
t
+
V
4
t
+
V
5
t
其中,
V
t
+
1 为下个周期个体鱼的游动方向,
V
1
t 为周期t中该个体鱼的游动方向,
V
2
t 为周期t当前个体到邻居平均位置的方向,
V
3
t 为邻居的平均方向,
V
4
t 为小于碰撞距离的邻居到当前个体方向的平均值,
V
5
t 为避险方向。考虑到各规则对鱼的影响力不同,我们还需要对各个方向加权,取加权平均值,权重的大小可以根据不同鱼类来确定。
V
t
+
1
=
λ
1
V
1
t
+
λ
2
V
2
t
+
λ
3
V
3
t
+
λ
4
V
4
t
+
λ
5
V
5
t
其中,
λ
1
+
λ
2
+
λ
3
+
λ
4
+
λ
5
=
1 。
每条沙丁鱼下一刻游动的方向都要受这五个因素的影响,将这五个方向的平均作为人工鱼下一刻游动的方向如图6。
Figure 6. The swimming direction of the next sardine
图6. 沙丁鱼下一刻的游动方向
1) 靠近规则的实现:每个个体都有向邻居中心靠拢的特性,邻居中心为观察范围内各个体所在位置的平均值。公式表示为:
V
¯
=
∑
V
i
N
(
i
∈
N
)
V
2
t
=
(
x
¯
−
x
0
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
,
y
¯
−
y
0
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
,
z
¯
−
z
0
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
)
V
¯
(
x
¯
,
y
¯
,
z
¯
) 为邻居的平均值,
P
0
(
x
0
,
y
0
,
z
0
) 为当前个体的位置,
P
i 为当前各个邻居的位置。
2) 对齐规则的实现:沙丁鱼会和它的邻居朝同一个方向游动。公式表示为:
V
3
t
=
∑
V
i
|
N
|
(
i
∈
N
)
V
i 为各个邻居的方向,N为邻居的个数,
V
3
t 为邻居的平均方向。
3) 避免碰撞规则的实现:当个体和它的邻居靠的太近时(距离小于碰撞距离),应自动避开。公式表示为:
V
4
t
=
∑
(
(
x
¯
−
x
0
)
/
|
M
|
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
,
(
y
¯
−
y
0
)
/
|
M
|
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
,
(
z
¯
−
z
0
)
|
M
|
(
x
¯
−
x
0
)
2
+
(
y
¯
−
y
0
)
2
+
(
z
¯
−
z
0
)
2
)
(
i
∈
M
)
V
4
t 为小于碰撞距离的邻居到当前个体方向的平均值,M为邻居中小于碰撞距离的邻居个数。
4) 由于沙丁鱼在运动中有一定的速度,在上一个周期的运动方向对下一周期的运动产生一定的影响。该影响与沙丁鱼的运动速度成正相关,因为假设沙丁鱼速度为常值,此处,惯性影响也假设为常值,用
V
1
t 表示。
5) 结合威胁源的特点,增加了“威胁躲避”对游动方向影响的分析。当海豚靠近沙丁鱼,出现在沙丁鱼的感知范围内时,沙丁鱼将产生避险意识,避险方向为海豚到沙丁鱼的方向,同时向其感知范围内相邻的沙丁鱼发送告警信号,接受到告警信号的沙丁鱼将产生离散意识,离散方向为其感知到的避险沙丁鱼游动方向的平均方向。则此时沙丁鱼的游动方向,公式表示为:
V
5
t
=
arctan
y
0
−
y
5
t
x
0
−
x
5
t
3.2. 模型
3.2.1. 沙丁鱼群运动模型
力是改变物体的运动状态的原因,现我们假设各种作用对群体的影响为一种抽象的力,将内部作用的影响分为三种力:吸引力、排斥力和一致力,而将外部作用分为两种力:诱惑力和危险力。其中诱惑力对于沙丁鱼主要为食物诱惑,题目中没要求暂且不考虑。而威胁力主要为海豚捕食造成的。设定当沙丁鱼群不受外部作用力(只受自身内部作用力影响)时处于平衡态。
1、当鱼群处于平衡态时
Figure 7. Schematic diagram of the internal scope of the population model
图7. 群体模型内部作用范围示意图
如图7所示,三个圆的半径分别为r1,r2,r3。则个体沙丁鱼的排斥区域为
0
−
r
1 ,个体沙丁鱼的协同区域为
r
1
−
r
2 ,个体沙丁鱼的吸引区域为
r
2
−
r
3 ,距离r3之外不属于个体的感知范围。
排斥区域——在这个距离之内的其他个体对此个体有排斥作用,即此个体希望远离排斥区域内的其他个体。
协同区域——在这个范围内的其他个体对此个体总保持协同运动或保持一致运动的趋势。
吸引区域——在此区域的其他个体对此个体有吸引作用,即此个体希望向它们靠近。
2、当鱼群处于非平衡态时(海豚个体对鱼群运动的影响)
1) 建立粒子群
假设在一个D维的目标搜索空间中,有N个粒子组成一个群落,其中第i粒子表示为一个D维的向量:
X
i
=
(
x
i
1
,
x
i
2
,
⋯
,
x
i
D
) ,
i
=
1
,
2
,
3
,
⋯
,
N
第i个粒子的“飞行”速度也是一个D维的向量,记为:
V
i
=
(
v
i
1
,
v
i
2
,
⋯
,
v
i
D
) ,
i
=
1
,
2
,
3
,
⋯
,
N
第i个粒子迄今为止搜索到的最优位置称为个体极值,记为:
p
b
e
s
t
=
(
p
i
1
,
p
i
2
,
⋯
,
p
i
D
) ,
i
=
1
,
2
,
3
,
⋯
,
N
整个粒子群迄今为止搜索到的最优位置为全局极值,记为:
g
b
e
s
t
=
(
p
g
1
,
p
g
2
,
⋯
,
p
g
D
) ,
i
=
1
,
2
,
3
,
⋯
,
N
在找到这两个最优值时,粒子根据如下的公式(2.1)和(2.2)来更新自己的速度和位置
v
i
d
=
w
∗
v
i
d
+
c
1
r
1
(
p
i
d
−
x
i
d
)
+
c
2
r
2
(
p
g
d
−
x
i
d
)
x
i
d
=
x
i
d
+
v
i
d
其中:
c
1 和
c
2 为学习因子,也称加速常数,
r
1 和
r
2 为[0,1]范围内的均匀随机数。式(1)右边由三部分组成,第一部分为惯性或动量部分,反映了粒子的运动习惯,代表粒子有维持自己先前速度的趋势;第二部分为认知部分,反映了粒子对自身历史经验的记忆或回忆,代表粒子有向自身历史最佳位置逼近的趋势;第三部分为社会部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向群体或邻域历史最佳位置逼近的趋势,根据经验,通常
c
1
=
c
2
=
2 。
i
=
1
,
2
,
D 。
v
i
d 是粒子的速度,
v
i
d
∈
[
−
v
max
,
v
max
] ,vmax用来限制粒子的速度。
r
1 和
r
2 是介于[0,1]之间的随机数。
2) 确定算法的流程:
① 初始化粒子群,包括群体规模n,每个粒子的位置
x
i 和速度
v
i ;
② 计算每个粒子的适应度值
F
i
t
[
i
] ;
③ 对每个粒子,用它的适应度值
F
i
t
[
i
] 和个体极值
p
b
e
s
t
(
i
) 比较,如果
F
i
t
[
i
]
>
p
b
e
s
t
[
i
] ,则用
F
i
t
[
i
] 替换掉
p
b
e
s
t
[
i
] ;
④ 对每个粒子,用它的适应度值
F
i
t
[
i
] 和全局极值值
g
b
e
s
t 比较,如果
F
i
t
[
i
]
>
p
b
e
s
t ,则用
F
i
t
[
i
] 替
g
b
e
s
t ;
⑤ 根据公式(1),(2)更新粒子的速度
v
i 和位置
x
i ;
⑥ 如果满足结束条件(误差足够好或到达最大循环次数)退出,否则返回②。
3) 粒子群优先算法的数学表达:
在这一问的处理中,我们考虑到了海豚捕食范围的大小,这样来看,为了避免被捕食,粒子群中的每个沙丁鱼个体都需要改变速度的大小和方向来逃离海豚的捕食范围,但是由于沙丁鱼个体对于危险的感知是有一定范围的,在感知范围之外,仍然按照原来的方式行动。
定义密度最大点为海豚冲向集群时集群已经发现的最佳位置,即全局极值
![]() ,为了让海豚能够捕到猎物,我们设定海豚的最大速度
,为了让海豚能够捕到猎物,我们设定海豚的最大速度
v
max 大于粒子群中沙丁鱼的最大速度
v
max ;对每个个体确立一个行为原则,即在感知范围内,粒子群中沙丁鱼个体都尽量朝远离海豚的方向,那么粒子的方向为远离海豚的方向与周围平均方向的矢量和,大小为最大速度。将上述改进中跟数学有关的内容用数学表达式与示意图如图8:
Figure 8. Dolphin predation range and sardine escape
图8. 海豚捕食范围与沙丁鱼逃逸示意图
{
d
p
→
=
O
′
g
b
e
s
t
¯
v
p
=
v
′
max
(
O
′
O
≤
R
1
+
R
2
) (3)
{
v
i
j
(
t
)
=
w
v
i
j
(
t
−
1
)
+
φ
r
(
p
f
j
(
j
)
,
j
)
−
X
i
j
(
t
−
1
)
(
O
′
O
≤
R
1
+
R
2
)
v
i
j
=
v
max
d
→
(
t
+
Δ
t
)
=
O
′
O
+
d
(
t
)
→
(
O
′
O
≥
R
1
+
R
2
) (4)
1、当
R
1
+
R
2
≥
O
′
O 时
函数表达式(3)表示的是捕食者的运动速度大小和方向,
![]() 是捕食者的中心位置,dp是捕食者的运动方向,
是捕食者的中心位置,dp是捕食者的运动方向,
O
′
g
b
e
s
t
¯ 表示从捕食者中心指向集群全局最佳位置的方向向量。表达式即表示捕食者一旦被发现就开始猛冲捕食。
2、当
R
1
+
R
2
≤
O
′
O 时
函数表达式(4)表示的是集群中个体运动速度大小和方向。O是集群中个体的中心位置,d(t)表示集群中个体的运动方向。其中,
O
′
O
>
R
1
+
R
2 时,集群中个体运动方式与模型一中相同;
O
′
O
≤
R
1
+
R
2 时,则开始以最大速度开始躲避行为。
3.2.2. 相互配合的海豚捕捉沙丁鱼模型(多只海豚对沙丁鱼群的影响)
1、粒子群算法对运动情况的分析
在这种情况下,主要是进行对之前模型的改进,加入新的控制因素来影响粒子群中个体的速度大小或方向。
前面的模型中都是没有信息拥有者的情况,而且每个个体的地位相同。但是往往在一个群体中,某一个或者几个个体拥有更大的信息量,因而会对整个群体的行为产生比较大的影响。假设信息拥有者按照某个固定的方向游动,在整个游动过程中不受其他个体的影响,但信息拥有者的行为会影响其他个体,从而使得系统中其他个体与信息拥有者同步。信息拥有量多的为领导者,它能引导群体活动。例如,在本题目中,海豚中的领导者引导海豚分工合作,一部分形成包围圈,一部分围捕海豚,效率颇高,改进了海豚个体捕鱼的方式,更容易在大自然中生存下来。
海豚在群体中比单独行动时能更多更快地找到食物。如果海豚群中的一个成员找到了食物,其他成员也可以捕食。当海豚中各成员之间通过声呐来感应彼此的距离,当它们集体运动时,搜索沙丁鱼的面积最大。针对海豚群体觅食的特点,下面结合粒子群算法和群体运动模型(即相互配合的海豚捕捉沙丁鱼模型)来实现海豚相互配合围捕沙丁鱼群的行为。
设海豚在3维的目标空间搜索食物,群体规模为n,其中领导者在空间中的位置xk运动速度vk定义为:
x
k
=
(
x
k
1
,
x
k
2
,
x
k
3
)
T
,
k
=
1
,
2
,
3
,
⋯
,
n
v
k
=
(
v
k
1
,
v
k
2
,
v
k
3
)
T
,
k
=
1
,
2
,
3
,
⋯
,
n
领导者在空间中所搜索到的最佳食物位置记为
p
k
=
(
p
k
1
,
p
k
2
,
p
k
3
)
T ,也将其称为
p
b
e
s
t ,在群体中所有信息所有者经历过的最佳位置,即整个粒子群迄今为止搜索到的最优位置记为
p
g
=
(
p
g
1
,
p
g
2
,
p
g
3
)
T ,也称
g
b
e
s
t 。
以搜索食物的最优位置为目标,调整信息拥有者在
t
+
1 时刻的位置
x
k
(
t
+
1
) 和运动方向
为:
![]()
x
k
t
+
1
=
x
k
t
+
v
k
t
+
1
注:1)
k
=
1
,
2
,
⋯
,
n ,w为惯性权重。
2)
c
1 和
c
2 为加速常数。
3)
r
1 和
r
2 为两个在[0,1]范围内服从均匀分布的随机变量。
4) 迭代终止条件根据具体问题选为海豚迄今为止搜索到的最优位置满足的预定最小适应阈值。
5)
c
1 、
![]() 和w的取值会直接影响到算法的最终结果。对与感应能力灵敏的海豚,
和w的取值会直接影响到算法的最终结果。对与感应能力灵敏的海豚,
、
c
2 和w更是海豚围捕沙丁鱼群运动中不可忽略的部分。
2、海豚的相配合捕食策略
1) 如果沙丁鱼群的数量过多,超过海豚群体的围捕能力,那么海豚将先对沙丁鱼群进行分割。海豚群体从竖直方向将沙丁鱼群切割成围捕能力数量之内的部分,切割完成后两部分沙丁鱼群恢复成球状,海豚向着在围捕能力之内的沙丁鱼群进行围捕。
2) 十分讲究排兵布阵,兵分几路,一部分摆出一个口袋型的包围圈,一部分海豚充当“轰赶者”,将猎物向包围圈中驱赶,防止沙丁鱼扩散逃跑。
3) 由于海豚是哺乳动物,需要经常靠近海面进行换气,所以不能长时间潜入海底。若有n条海豚,其中n − 1条在沙丁鱼群下方防止沙丁鱼群逃向海底,并逐渐使沙丁鱼群向中心靠拢,海豚和沙丁鱼从俯视方向看运动方向都是逆时针;其中1条海豚在沙丁鱼群上部,防止沙丁鱼从上部逃散,同样使沙丁鱼群逐渐聚拢。当鱼群半径r逐渐缩小,沙丁种群密度不断增大,并与n成一定关系的时候,上方的海豚开始捕食沙丁鱼,下方的海豚继续围捕,使鱼群继续聚拢。
4) 当上方海豚吃饱之后,下方某一条海豚开始顶替上方海豚的位置,进行换班捕食。下方海豚继续使沙丁鱼逐渐靠拢,使得海豚群体中每一条海豚都能进行捕食。
3.3. 模型求解(MATLAB图像分析和分析方法)
3.3.1. 具体绘制方法
表示方法:为了明显区分不同鱼群,对于沙丁鱼群我们用蓝色表示;对于海豚,我们用红色表示。
3.3.2. 沙丁鱼群运动模型(海豚个体对沙丁鱼群运动影响)
表示方法:为了明显区分不同鱼群,对于沙丁鱼群我们用蓝色表示;对于海豚,我们用红色表示。
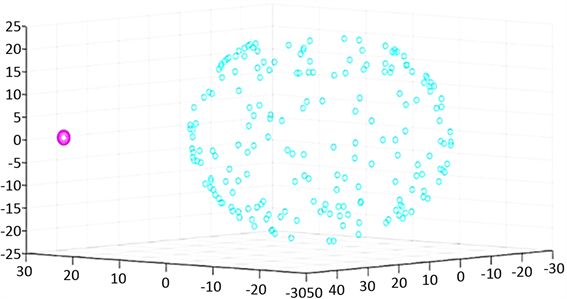
海豚个体对沙丁鱼的运动影响描述:最初,如图9所示,三维图的中心为初始沙丁鱼球形集聚的中心,海豚从远处开始接近。沙丁鱼的点满足点与点之间距离要超过r1,但是不超过r海豚随机出现在离沙丁鱼中心接近2 r的地方;海豚接近沙丁鱼群,如图10所示,海豚声波定位发现沙丁鱼群,并以最大速度向鱼群运动,直到声波定位失效,开始以自身侧线在一定范围的感知作用内感知到沙丁鱼。海豚寻找切入点,如图11所示,通过观看相关视频得知,海豚会先围绕沙丁鱼群,通过感知找到鱼群相对密度比较大的位置开始进行捕食。在三维图上,当海豚可以感知到沙丁鱼,而沙丁鱼感知不到海豚时,紫红点会围绕密集的蓝点旋转,直到找到蓝点密度较大的位置,向次方位运动,直到有沙丁鱼感知到海豚。海豚捕食,如图12所示,运用迭代的思想,感知道海豚的沙丁鱼下一步动作将由海豚的此时的位置决定,而其他的沙丁鱼的动作由此时运动的沙丁鱼决定,海豚的动作由海豚感知范围内的沙丁鱼数量决定,这样相互影响,一步步的迭代形成运动。在运动过程中,我们给海豚以疲劳值来决定是否继续捕食沙丁鱼。海豚离开:如图13所示,同样运用迭代的思想,不过这一次海豚的疲劳值决定不再捕食,海豚将以一个随机的速度离开,而沙丁鱼继续迭代,直到海豚离开所有沙丁鱼的感知范围。
Figure 9. Initialization of sardines and dolphins
图9. 初始化沙丁鱼群和海豚
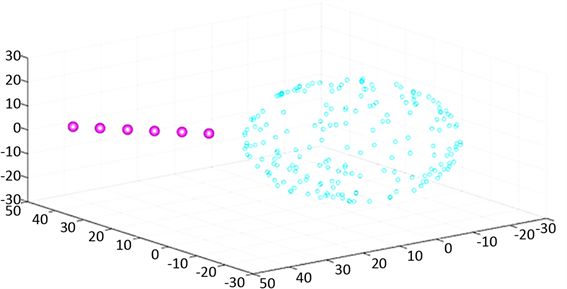
Figure 10. Dolphins begin to approach sardines
图10. 海豚开始接近沙丁鱼
Figure 11. Dolphins looking for entry points
图11. 海豚寻找切入点
Figure 12. The first iteration
图12. 第一次多次迭代
Figure 13. Repeated multiple times
图13. 第二次多次迭代
3.3.3. 相互配合的海豚捕食沙丁鱼模型
1、运动1——海豚接近沙丁鱼群:
海豚声波定位发现沙丁鱼群,并以最大速度向鱼群运动,直到声波定位失效,开始以自身侧线在一定范围的感知作用内感知到沙丁鱼。依照沙丁鱼的躲避习性,将会往海底运动,而海豚也有应对的经验,从沙丁鱼群的下部围捕沙丁鱼,沙丁鱼因为躲避而聚集。
2、运动2——海豚对沙丁鱼群进行切割:
如果沙丁鱼群的数量过多,超过海豚群体的围捕能力,那么海豚将先对沙丁鱼群进行分割。海豚群体从竖直方向将沙丁鱼群切割成围捕能力数量之内的部分,切割完成后两部分沙丁鱼群恢复成球状,海豚向着在围捕能力之内的沙丁鱼群进行围捕。由于海豚是哺乳动物,需要经常靠近海面进行换气,所以不能长时间潜入海底。若有n条海豚,其中n − 1条在沙丁鱼群下方防止沙丁鱼群逃向海底,并逐渐使沙丁鱼群向中心靠拢,海豚和沙丁鱼从俯视方向看运动方向都是逆时针;其中1条海豚在沙丁鱼群上部,防止沙丁鱼从上部逃散,同样使沙丁鱼群逐渐聚拢。当鱼群半径r逐渐缩小,沙丁种群密度不断增大,并与n成一定关系的时候,上方的海豚开始捕食沙丁鱼,下方的海豚继续围捕,使鱼群继续聚拢。
4. 模型的评价
4.1. 模型的优点
1) 充分考虑了实际情况,对个体鱼、鱼群行为运动进行了分析和求解。
2) 灵活运用了Matlab等数学软件,进行最模型仿真。
3) 对研究鱼群行为问题提供了借鉴作用。
4) 参考了粒子群算法和鱼群算法的思想,在Vicsek动物群模型和Bold动物群模型的基础上得出了能表示动物群运动的通用模型。通过调整不同作用力的系数大小就可以表示出动物群的觅食、聚群和躲避天敌等运动。具有创新性和通用性。
5) 用几何向量语言描述鲨鱼和沙丁鱼个体的位置变化情况,将鱼群逃逸这一行为数学化、向量化,语言准确科学。整个求解过程中,惯性权重w、加速因子
c
1 和
c
2 和最大速度
v
max 共同维护粒子对全局和局部搜索能力的平衡。PSO的一个优势就是采用实数编码,不需要像遗传算法一样采用二进制编码(或者采用针对实数的遗传操作)。粒子具有“记忆”的特性,它们通过“自我”学习和向“他人”学习,使其下一代具有针对性的从“先辈”那里继承更多的信息,从而能在较短的时间内找到最优解。粒子群优化算法的信息共享机制是很不同的,在粒子群优化算法中,信息流动是单向的,即只有
g
b
e
s
t 将信息给其他的粒子,这使得整个搜索更新过程跟随当前解。
6) 由海豚个体推广到多只海豚配合,优化性更强。
7) 建立的模型由个体到整体,层层递进,条理清晰,便于理解。
4.2. 模型的缺点
1) 文章将动物群的信息传递机制体现在吸引力、排斥力和一致力三个方面,讨论还不够深入问题一加入惯性运动和非惯性运动,使得模型过于细化。
2) 模型中参数的调整主观性较强。
3) 未对沙丁鱼与海豚的交互空间进行严密的分析。
4) 对于一些问题的研究不够专业。
5) 单单考虑距离的影响进行迭代,忽略了水流,光线等因素的干扰。
6) 由于PSO中粒子向自身历史最佳位置和邻域或群体历史最佳位置聚集,形成粒子种群的快速趋同效应,容易出现陷入局部极值、早熟收敛或停滞现象。同时,PSO的性能也依赖于算法参数。
7) 实验假设比较理想,比如将沙丁鱼和海豚都设置成了点来进行模拟仿真。
8) 实验数据都是经过资料查询进行假设的,与现实中的海豚围捕沙丁鱼群还是有一定的差距。