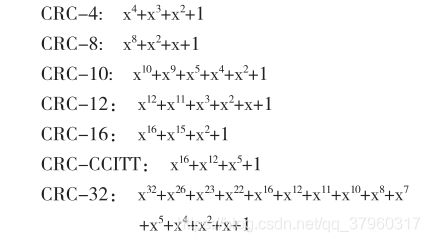CAN总线的CRC校验

1.CRC原理

1.1生成多项式

理解CRC校验，首先需要了解生成多项式的概念，生成多项式也就是发送方和接受方约定的一个除数而已，发送方和接收方都使用这一个相同的除数进行模2运算，计算结果相同则说明传输数据没有问题，而如果计算结果不同可能传输的数据就出现了问题，目的就是为了保证数据传输的可靠性。

上面提到的模二计算本质上就是异或运算，相同的位为0，不同的位为1，也就是不考虑进位、错位的二进制加减法运算，例如：10011011 + 11001010 = 01010001.

常见的生成多项式：

CRC8 = X8 + X5 + X4 +1

CRC16 = X16 + X15 + X5 +1

CRC12 = X12 + X11 + X3 + X2 + 1

CRC32 = X32 + X26 + X23 + X22 + X16 + X12 + X11 + X10 + X8 + X7 + X5 + X4 + X2 + X1 + 1

每一个生成多项式都是与一个代码相对应的，比如CRC8对应的代码就是100110001

1.2通讯校验的过程

假设被处理的报文的多项式为P(X)，收发双方约定的多项式为G(X)，使用P(X)除以G(X)求得余数多项式R(X)，并将余数多项式R(X)附加到被处理报文多项式P(X)后，生成M(X)，按照此计算，M(X)除以G(X)的余数应该是0，然后将M(X)发送给接收方，假设接收方接收的报文为N(X)，除以同样的除数G(X)，余数应该也是零，如果结果为零说明发送和接收序列一致，否则传输出现了问题。

举例说明：

假设待发送的信息为1011001，对应的多项式为X6+X4+X3=1，若选取约定多项式为G(X)=X4+X3+1，其对应的代码为11001，然后使用模二算法求出余数多项式，如下所示：

求余数之前需要将发送消息的生成多项式乘以约定多项式的最高次幂以后做被除数，然后求得的余数为1010，将余数1010附加到发送消息的后边，则发送消息变为10110011010。

接收方接收此数据后，再做除数运算，余数应该为0。

1.3CAN总线中使用的生成多项式

前面讲述了CRC校验的基本规律，而在CAN通讯中使用的CRC算法和一般的算法的区别就是生成多项式不同，计算的方式是相同的。

通过下面一个图可以看出不同的CAN使用的生成多项式的差异

传统CAN使用的是CRC15的算法，这个通过CAN的数据结构也可以看出，CRC段的长度就是15位。CAN FD之所以有两种是因为CAN FD的数据长度是可变的，针对不同的数据长度使用的方法不同，低于16字节的使用的是CRC17，高于16字节的使用的是CRC21。

2.CRC串行实现

根据1.2节的模2运算过程，可以推出CRC16串行实现步骤为：
（1）预制一个16位的存储空间CRC，并赋初始值

（2）将要发送的数据打包成一个Byte数组（将数据分成多个Byte存储）

（3）将第一个数据左移8位并与CRC当前值进行异或，结果放入CRC

（4）判断当前CRC的最高位（MSB）是否为1，若为1，则左移一位，将MSB移出，并在LSB（最低位）补0，将新的数据与简记式Poly进行异或，结果存入CRC；若MSB为0则只进行左移操作。

（5）重复步骤3-4直至8个数据移动完毕，此时CRC中的值就是我们要的校验码。

假设数据为0xAA，多项式为8005（最高位1省略），初始值0x00，输出异或值0x00。下图可以证明上述步骤的实现过程的正确性：

3.CRC并行实现

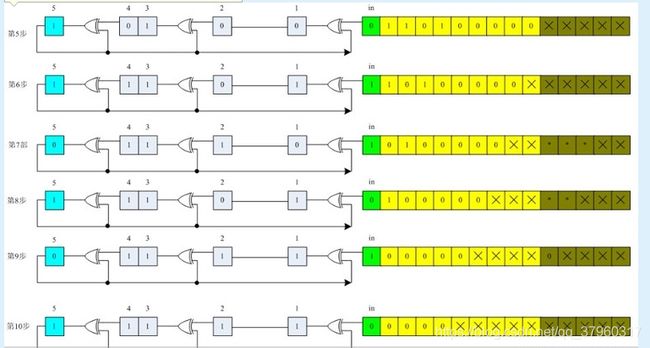
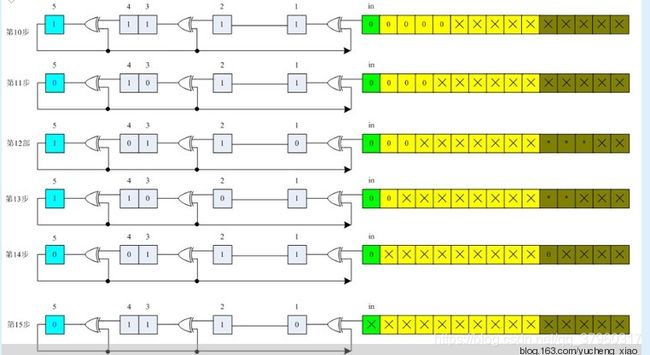
3.1CRC模2运算及LFSR实现

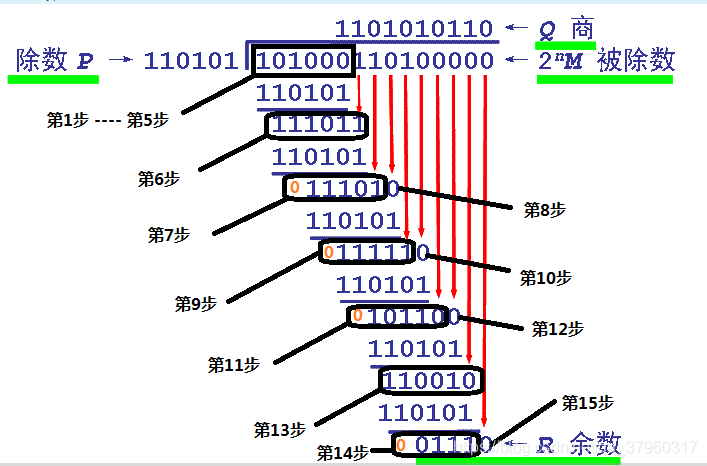
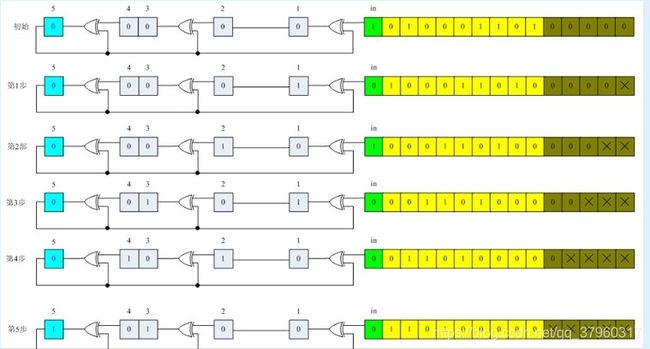
设需要发送的信息为M = 1010001101，产生多项式对应的代码为P = 110101，R＝5。在M后加5个0，然后对P做模2除法运算，得余数r(x)对应的代码：01110。故实际需要发送的数据是101000110101110。
对应多项式为110101 即 x5+ x4+ x2+1。
模2除运算过程如下：

LFSR运算过程如下：

3.2CRC代码实现

如果用时序电路串行实现，则8 bit数据要移位8次，就需要8个clk，效率低下，为了能在一个时钟周期输出结果，必须采用组合电路，当然，这是以空间换时间的方法！

以一种CRC16 为例，说明其实现方式，参数如图所示。

CRC16 的多项式为：

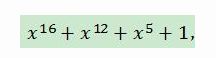
LFSR电路图如下，需要注意的是，数据移入顺序是先高后低。以8bit数据为例，其数据处理顺序是Data[7]->Data[0]，这也是为什么，第一个例程中使用了for(i=7; i>=0; i=i-1)的原因。

两种Verilog实现方式，结果完全一致。

module CRC_GEN(
    input            rst,     /*async reset,active low*/
    input            clk,     /*clock input*/
    input     [7:0]  data_in, /*parallel data input pins */
    input            d_valid, /* data valid,start to generate CRC, active high*/
    output reg[15:0] crc
);

integer i;
reg feedback;
reg [15:0] crc_tmp;
/*
*　　sequential process
*/
always @(posedge clk or negedge rst)
begin
    if(!rst) 
        crc <= 16'b0;          /*触发器中的初始值十分重要 */
    else if(d_valid==1'b0)
        crc <= 16'b0;
    else
        crc <= crc_tmp;
end

/*
*   combination process
*/
always@( data_in or crc)
begin
    crc_tmp = crc;
    for(i=7; i>=0; i=i-1)
    begin
        feedback    = crc_tmp[15] ^ data_in[i];
        crc_tmp[15]  = crc_tmp[14];
        crc_tmp[14]  = crc_tmp[13];
        crc_tmp[13]  = crc_tmp[12];
        crc_tmp[12]  = crc_tmp[11] ^ feedback;
        crc_tmp[11]  = crc_tmp[10] ;
        crc_tmp[10]  = crc_tmp[9];
        crc_tmp[9]   = crc_tmp[8];
        crc_tmp[8]   = crc_tmp[7];
        crc_tmp[7]   = crc_tmp[6];
        crc_tmp[6]   = crc_tmp[5];
        crc_tmp[5]   = crc_tmp[4] ^ feedback;
        crc_tmp[4]   = crc_tmp[3];
        crc_tmp[3]   = crc_tmp[2];
        crc_tmp[2]   = crc_tmp[1];
        crc_tmp[1]   = crc_tmp[0];
        crc_tmp[0]   = feedback;
     end
end

endmodule

module CRC16_D8;

  // polynomial: x^16 + x^15 + x^2 + 1
  // data width: 8
  // convention: the first serial bit is D[7]
  function [15:0] nextCRC16_D8;

    input [7:0] Data;
    input [15:0] crc;
    reg [7:0] d;
    reg [15:0] c;
    reg [15:0] newcrc;
  begin
    d = Data;
    c = crc;

    newcrc[0] = d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[3] ^ d[2] ^ d[1] ^ d[0] ^ c[8] ^ c[9] ^ c[10] ^ c[11] ^ c[12] ^ c[13] ^ c[14] ^ c[15];
    newcrc[1] = d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[3] ^ d[2] ^ d[1] ^ c[9] ^ c[10] ^ c[11] ^ c[12] ^ c[13] ^ c[14] ^ c[15];
    newcrc[2] = d[1] ^ d[0] ^ c[8] ^ c[9];
    newcrc[3] = d[2] ^ d[1] ^ c[9] ^ c[10];
    newcrc[4] = d[3] ^ d[2] ^ c[10] ^ c[11];
    newcrc[5] = d[4] ^ d[3] ^ c[11] ^ c[12];
    newcrc[6] = d[5] ^ d[4] ^ c[12] ^ c[13];
    newcrc[7] = d[6] ^ d[5] ^ c[13] ^ c[14];
    newcrc[8] = d[7] ^ d[6] ^ c[0] ^ c[14] ^ c[15];
    newcrc[9] = d[7] ^ c[1] ^ c[15];
    newcrc[10] = c[2];
    newcrc[11] = c[3];
    newcrc[12] = c[4];
    newcrc[13] = c[5];
    newcrc[14] = c[6];
    newcrc[15] = d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[3] ^ d[2] ^ d[1] ^ d[0] ^ c[7] ^ c[8] ^ c[9] ^ c[10] ^ c[11] ^ c[12] ^ c[13] ^ c[14] ^ c[15];
    nextCRC16_D8 = newcrc;
  end
  endfunction
endmodule

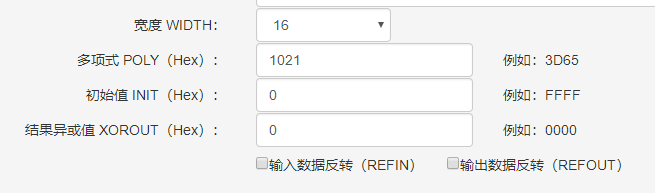
4.CRC生成工具

CRC Genaration Tool）

5.参考文章

1.详解LIN通讯和CAN通讯的校验算法
2.CRC校验原理及实现
3.关于CRC校验实现程序解释（CRC16为例）
4.基于FPGA的CRC校验码生成器）