【扩散模型】3、DDIM | 加速 DDPM 的采样速度

论文：Denoising Diffusion Implicit Models

代码：https://github.com/CompVis/stable-diffusion/blob/main/ldm/models/diffusion/ddim.py

出处：ICLR 2021

时间：2021.10.05

DDIM 贡献：

• 指出 DDPM 中的 $L_{sample}$ 与扩散过程的联合分布具体形式无直接关系，所以训练 $L_{sample}$ 就相当于训练了一系列潜在的扩散模型
• 构造了一种更具有一般性的马尔科夫扩散过程，并且让其满足边缘分布不变，以能够重复利用训练好的 DDPM 模型
• 构造了一种更具有一般性的采样算法
• 提出了 respacing 的技巧来减小采样步骤，在训练 $L_{sample}$ 的时候，和联合分布无关，所以可以跳过一些步骤来采样， DDIM 可以以 5 倍少的步骤获得和 DDPM 一样的采样质量

知乎介绍

公众号介绍

B 站：https://www.bilibili.com/read/cv25126637/

DDPM: https://zhuanlan.zhihu.com/p/638442430

DDIIM : https://www.zhangzhenhu.com/aigc/ddim.html#equation-eq-ddim-226

非马尔科夫：https://zhuanlan.zhihu.com/p/627616358

bilibili：https://www.bilibili.com/video/BV1JY4y1N7dn/?spm_id_from=333.337.search-card.all.click&vd_source=dff5a38233d0daec447c275bf4070791

一、背景

DDPM 没有使用对抗网络且获得了很好的图像生成效果，但由于在逆向去噪时需要进行多次的采样（约 1000 次），才能产生较好的生成结果。

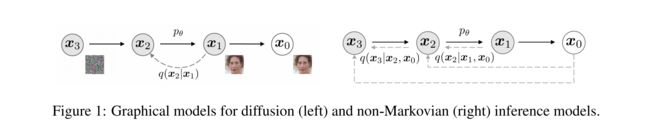
DDPM 的前向加噪过程是马尔科夫过程，也就是当前时刻的状态只和上一时刻的状态有关，DDPM 的反向去噪过程是马尔科夫的逆过程

这和扩散模型的原理有很大的关系，基于扩散模型的生成方式就是逐步从噪声中一步步还原出图片，正向扩散多少步，逆向去噪也需要多少步，和 GAN 相比就很慢，GAN 只需要一次就可以了生成需要的图片

• DDPM：大概需要 20h 才能采样生成 50k 个 32x32 的图片（大概需要 1000h 才能生成 50k 个 256x256 的图片）
• GAN：大概需要 1min

为了提高 DDPM 的采样速度，本文作者提出了 denoising diffusion implicit models (DDIMs)，和 DDPM 的目标函数是一样的，DDIM 将前向过程构造为非马尔科夫过程，那么反向过程也是非马尔科夫过程的逆过程，也正是因为这种非马尔科夫过程的方式，决定了 DDIM 的生成过程能够更确定，能够更快速度生成高质量样本，在计算量和采样质量上更平衡。

DDIM 为什么能加速：

DDIM 能对 DDPM 加速 10x~50x，为什么能加速的原因在于其使用的非马尔科夫过程，因为 DDPM 前向和逆向需要同样的步数的原因在于其使用的马尔科夫过程决定了其只能这么做，DDIM 不使用马尔科夫过程后，就能够跳过一些步骤啦，即跳步采样

DDIM 的特点：DDIM 和 DDPM 很类似，训练的目标函数也是相同的，所以能直接用 DDPM 训练好的模型，修改一下采样过程就能用了

• 反向过程使用非马尔科夫链过程：DDPM 的前向和反向的每一步都是马尔科夫链的过程，也就是当前时刻的结果 $x_{t-1}$ 只依靠前一时刻的值 $x_t$ ，但 DDIM 在反向使用的是非马尔科夫链过程，也就是当前时刻同时依靠 $x_t$ 和 $x_0$ ，能够使用更少的步数来生成图片，提高采样的效率（10~50倍加速）
• 有更好的一致性：只要初始值一样，使用不同步长生成的样本最后的高层特征也是相似度的，生成过程是确定的
• 可以使用插值：由于 DDIM 的生成结果有很好的一致性，所以能获得有意义的语义插值

二、DDIM 如何改进

2.1 DDPM 的原理回顾

DDIM 和 DDPM 有一些符号使用的不同，需要注意

• DDPM 中的 ${\overline{\alpha }}_t$ 在 DDIM 中的表示是 ${\alpha }_t$

给定一个数据分布 $q(x_0)$，能够通过采样产生一系列的样本，生成式模型关心的就是能够学习这个数据分布，学习的方式就是学习一个 $p_{\theta }(x_0)$ 来逼近 $q(x_0)$，当逼近效果足够好的时候，就可以从 $p_{\theta }(x_0)$ 中生成新的样本，这就是生成式模型

在 DDPM 中，其实就是以隐变量模型的形式来对数据分布进行建模，认为：

这里的联合分布就是后半部分的形式，就是一系列马尔科夫过程的乘积，生成式过程需要去模拟前向扩散那个马尔科夫过程的逆过程，这里的 $x_1$ 到 $x_T$ 和 $x_0$ 的大小都是一样的

DDPM 中的目标函数就是使得对数似然最大，是一个变分的模型，优化的是下界

DDPM 中，加噪的过程是使用马尔科夫链这种形式做的，也就是连乘的方式，并且条件分布 q 也是高斯分布，均值和方差如公式 3 所示

所以前向扩散过程是马尔科夫链，那么反向去噪的过程也是马尔科夫链，逼近的是一个逆过程 $q(x_{t-1}|x_t)$

对于前向扩散过程，有一个特殊的性质就是能够把 $q(x_t|x_0)$ 写出来，等价成一个新的正态分布，也是边缘分布

既然有这样的形式，所以 $x_t$ 和 $x_0$ 就能通过引入噪声 $ϵ$ 来表达：

当 ${\alpha }_T$ 设置的接近于 0 时，$q(x_T|x_0)$ 就会趋近于标准高斯分布，所以 $p_{\theta }(x_T):=N(0,I)$，也就是 $p_{\theta }(x_T)$ 的分布是接近于标准高斯分布的，所以就能初始化一个高斯分布，然后就能逐步采样出 $x_0$

DDPM 的目标函数如下，这也是将公式 2 重写的形式，这也是假设学习的高斯分布均值（方差是固定的），就可以写成是预测的噪声和真实噪声的差的平方，${ϵ}_t$ 是真实噪声，DDPM 中的系数 ${\gamma }_t=1$，当 ${\gamma }_t=1$ 时，这其实就是分数模型，也进一步说明了，要想用这种模式来训练模型，前向扩散过程不一定非要是马尔科夫过程，只要边缘分布满足公式 4 就可以了。

在 DDPM 中，为了让 $p_{\theta }(x_T)$ 更趋向于标准高斯分布 $N(0,I)$，也为了让加噪的过程和逆过程都是高斯分布，所以把 T 设置的比较大（1000），也是为了让生成过程近似为一个高斯分布，但是这个采样过程很耗时。

DDPM 损失函数的特点：

• 由于噪声是来自于 $q(x_t|x_0)$ 的采样，所以损失函数只由 $q(x_t|x_0)$ 决定，也证明了该损失函数是一个分数匹配的形式
• 也就是损失函数只依赖于边缘分布，不直接依赖于联合分布，就是说联合分布以什么样的形式出现并不会影响模型训练

所以，是不是存在非马尔科夫过程也能实现这种加噪方式，只需要保证 $q(x_t|x_0)$ 和 DDPM 的相同，而 $q(x_{1:T}|x_0)$ 可以不相同。所以能不能避免使用马尔科夫这种需要一步步反向递推的过程，而是直接使用更一般的形式 $q(x_t|x_{t-1},x_0)$，只要保证 $q(x_t|x_0)$ 不变即可。

所以 DDIM 的作者给出了一种非马尔科夫性质的前向扩散过程，和后验概率分布的表达方式，而该后验分布恰好满足 DDPM 中的边缘分布 $q(x_t|x_0)$ 。

2.2 DDIM 的非马尔科夫前向扩散过程

考虑一种新的分布，引入了一个新的参数 $\sigma$，是一个实数，大于等于 0，是超参数，不需要训练，但可以自定义这个值的大小

前向扩散过程被设计了一种新的方式（公式 6 ），后验分布仍然是高斯分布（公式 7）

基于公式 6 和 7 能证明，在任意时刻的 $q_{\sigma }(x_t|x_0)$ 仍然服从正态分布

证明过程：

总结：

• DDIM 的作者设计了一个非马尔科夫前向扩散过程，并且边缘分布仍然和 DDPM 中一样，就能够继续沿用 DDPM 的目标函数来训练网络

DDPM 和 DDIM 后验概率分布的对比：

• DDIM 多了一个超参数 $\sigma$，会影响后验分布，影响采样过程重参数化过程，因为用神经网络构建的分布是要逼近后验分布的，从这个后验分布中采样得到 t-1 时刻的样本，也就是要先算出这个预测的后验分布的均值和方差，然后使用重参数来计算噪声。超参数取值不同，就会影响重参数的计算，因为超参数不同，均值和方差不同，最后的结构就不同

2.3 非马尔科夫扩散逆过程的采样

接下来就是定义可训练的生成过程 $p_{\theta }(x_{0:T})$，每个 $p_{\theta }^{(t)}(x_{t-1}|x_t)$ 就是为了逼近 $q_{\sigma }(x_{t-1}|x_t,x_0)$，也就是说给定一个噪声样本 $x_t$ 先预测 $x_0$，然后再根据条件分布 $q_{\sigma }(x_{t-1}|x_t,x_0)$ 得到 $x_{t-1}$

DDPM 中是没有预测 $x_0$ 的，是预测的是噪声 $ϵ$

但其实如公式 4 所示，得到了噪声 $ϵ$ 后，能够反推出 $x_0$

所以，通过公式 4 ，将 $ϵ$ 和 $x_t$ 带入，算出 $f_{\theta }$，就是给定 $x_t$ 情况下，去噪观测量，也就是在当前 t 时刻预测出的 $x_0$，如公式 9 所示

根据预测的 $x_0$，就可以利用后验分布来作为逼近的目标，是分段的函数，t>1 时就是 $q_{\sigma }$ 的分布，t=1 时，期望是一个正态分布，如公式 10 所示

一种特殊的采样——DDIM： $\sigma =0$

下面的公式 12 就是本文提出的后验分布的重参数过程，就是从 $x_t$ 生成 $x_{t-1}$ 的过程，均值+标准差*噪音

不同的 $\sigma$ 就会导致均值不一样，标准差不一样，所以采样的结果肯定也不一样，但是目标函数是一样的，或者说模型 ${ϵ}_{\theta }$ 都是一样的，也就是说，对于不同的 $\sigma$，是不需要重新训练模型的， $\sigma$ 只影响采样的结果。

$\sigma$ 取下面的值的时候，就退化成了 DDPM 的生成过程（马尔科夫链的生成过程）

当 $\sigma =0$ 时，就是确定性的采样了，生成过程就是确定性的，因为随机项已经没有了，这个时候就是 DDIM 了

作者还推导了为什么 DDIM 可以直接使用 DDPM 的目标函数来训练：

总结 DDIM：

构建了一个更一般的非马尔科夫的过程，将超参数设置为 0 ，变成一个确定性采样的过程

2.4 加速采样 —— Respacing

上面的 DDIM 本身是一个模型，并没有加速，加速是因为可以在模型上引入一个技巧，且伤害性很小，所以能加速

DDPM 中，前向过程有 T 步，后向过程也要有 T 步，但是 L1（也就是 $L_{sample}$ 的过程其实并不依赖于前向过程，无论是不是马尔科夫链，只要 $q_{\sigma }(x_t|x_0)$ 是固定的就可以了。

所以作者就想加速采样，本来要从 1 ~ T 序列 $x_{1:T}$ 上逐步迭代，现在就从其中找到一个子集 $\{x_{{\tau }_1},x_{{\tau }_2},...,x_{{\tau }_S}\}$，共选择了 S 个作为子集

所以，定义前向过程 $q(x_{{\tau }_i}|x_0)=N(\sqrt{{\alpha }_{{\tau }_i}}{x}_0,(1-{\alpha }_{{\tau }_i})I)$ 匹配上之前定义的边缘分布，这样一来，生成过程就可以直接在子序列上去做。也就是说训练的时候是完整的序列，生成的时候是子序列，只要子序列小，且效果没有很差，所以就能加速。

三、效果