释放数据的潜力：用梯度上升法解锁主成分分析（PCA）的神奇

引言

主成分分析（PCA）是一种常用于降维和特征提取的技术，它有助于发现数据中的主要变化方向。虽然传统的PCA方法通常依赖于特征值分解或奇异值分解等数学技巧，但在本文中，我们将介绍一种不同的方法，即使用梯度上升来求解PCA问题。

---

什么是主成分分析（PCA）？

主成分分析是一种统计技术，旨在找到数据中的主要变化方向，以便将数据投影到新的坐标系中，从而减少维度或提取最重要的特征。通常情况下，PCA的目标是找到一组正交基向量（模长为1的向量），称为主成分，这些向量按照方差递减的顺序排列。这些主成分捕捉了数据中的大部分信息，允许我们以更低维度的方式表示数据。

---

传统PCA vs 梯度上升PCA

传统PCA方法依赖于特征值分解或奇异值分解等数学工具，这些方法在处理大规模数据集时可能效率较低。相比之下，梯度上升是一种优化技术，可用于直接最大化PCA的目标函数，即最大化数据在新坐标系中的方差。

---

PCA的优化目标

在传统PCA中，我们通过解决以下优化问题来找到主成分：

最大化目标函数：

其中，$\mathbf{w}$ 是主成分的权重向量，${\mathbf{x}}_i$ 是数据样本，$n$ 是样本数量。

代码实现

求解第一主成分

在实现之前我们需要做数据的准备工作

import matplotlib.pyplot as plt
import numpy as np
X = np.empty(shape=(100,2))
X[:,0] = np.random.uniform(0,100,size=100) # 生成0-100之间100个随机数
X[:,1] = 0.6*X[:,0]+5 + np.random.normal(0,10,size=100)

绘制后如下图

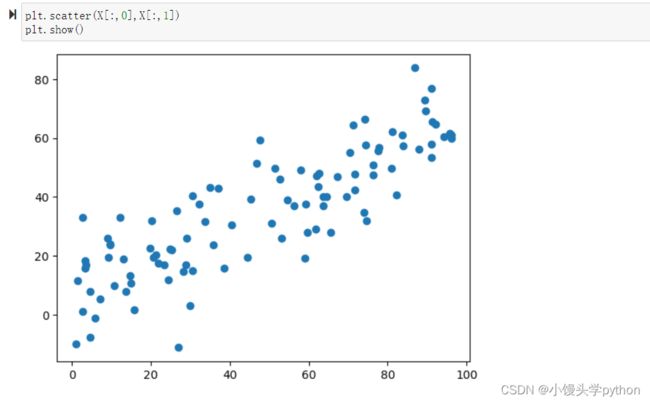
接下来我们需要创建一个函数demean目的是使得矩阵各个维度上的均值都为0

官方解释：这个函数的目的是将数据中的均值信息去除，以便更好地进行后续数据分析或建模，特别是当不同维度的尺度差异较大时，去均值操作可以有助于模型的性能提升。

def demean(X):
    return X-np.mean(X,axis=0)

• 使用 np.mean(X, axis=0) 计算 X 的每个维度（列）上的均值。axis=0 参数指定了沿着列的方向进行均值计算。

接下来需要创建一个效用函数，这里遵循梯度上升（寻找方差最大的效用函数）

def f(X,w): # 求方差最大的效用函数
    return np.sum(X.dot(w)**2)/len(X)

还需要一个求梯度的函数

def df(X,w): # 求梯度
    return X.T.dot(X.dot(w)) * 2. /len(X)

可以依照如下图示

接下来创建一个梯度上升的函数，和梯度下降的函数类似

def gradient_ascent(X,initial_w,eta=0.0001,n_iters=1e4,epsilon=1e-8): # eta取值比较小的原因是w的单位向量
	w = initial_w
    i_iter = 1
    while i_iter<=n_iters:
        last_w = w
        gradient = df(X,w)
        w = w+ gradient*eta
        if abs(f(X,w)-f(X,last_w))<epsilon:
            break
        i_iter+=1
    return w

注意：这里的w每次会发现变化，那就不是单位向量了，所以我们应该在每次函数执行的时候都应该将w设置成单位向量
修改后的梯度上升函数代码如下

def direction(w): # 每次求一个单位方向
    return w/np.linalg.norm(w)

def gradient_ascent(X,initial_w,eta=0.0001,n_iters=1e4,epsilon=1e-8): # eta取值比较小
    w = direction(initial_w)
    i_iter = 1
    while i_iter<=n_iters:
        last_w = w
        gradient = df(X,w)
        w = w+ gradient*eta
        w = direction(w)
        if abs(f(X,w)-f(X,last_w))<epsilon:
            break
        i_iter+=1
    return w

最后我们来测试一下

initial_w = np.random.random(X.shape[1])   # 这里不能取0
X_demean = demean(X)
w = gradient_ascent(X,initial_w)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.plot([0,w[0]*25],[0,w[1]*25],color='r')
plt.show()

运行结果如下

注意：对于PCA问题 不能使用数据标准化来处理数据这个轴就是一个主成分，是我们求出来的第一个主成分，所以叫他第一主成分，接下来我们求解第二主成分

求解第二主成分

在求解之前，我们可以先了解一下

第一主成分和第二主成分是PCA中的两个最重要的成分

联系：

• 都是主成分： 第一主成分和第二主成分都是数据中的主要变化方向，它们是原始数据中的线性组合，以便最大程度地捕捉数据的方差。

• 正交性： 第一主成分和第二主成分是正交的，即它们之间的内积为零。这意味着它们是彼此独立的方向，没有重叠。

• 降维： PCA的目标是将数据从原始高维空间投影到主成分构成的低维空间中。第一主成分通常包含最大的方差，第二主成分包含次大的方差，因此它们通常用于构建一个较低维度的表示来降低数据的维度。

区别：

• 方差： 第一主成分包含数据中的最大方差，而第二主成分包含次大方差。因此，第一主成分捕获了数据中的最大变化，而第二主成分捕获了除第一主成分之外的最大变化。以此类推，后续主成分包含的方差逐渐减小。

• 权重向量： 第一主成分和第二主成分是由不同的权重向量定义的。这些权重向量决定了如何将原始特征组合成主成分。第一主成分的权重向量是使得第一主成分方差最大化的方向，第二主成分的权重向量是使得第二主成分方差最大化的方向。

• 信息： 第一主成分通常包含最多的信息，因为它捕获了数据中的最大变化。第二主成分包含的信息次于第一主成分，但与第一主成分正交。因此，第一主成分和第二主成分合起来可以保留大部分原始数据的信息。

找到第一主成分之后，每一个样本都去 去掉第一主成分上的分量，对于这个结果 继续去求第一主成分，得到的就是第二主成分

这里可以举个例子，前一个得出的是纵轴的分向量，后一个是横轴的分向量

这里可以用下面的语句来表示去掉第一主成分分量以后的样本

X2 = X_demean-X_demean.dot(w).reshape(-1,1)*w

注意：如果特征值就两个，那么第一第二主成分是垂直关系，但是如果特征值多个的话就不一定了。

在sklearn中封装的PCA

这里我们简单演示一下取前两个和一个主成分
首先导入必要的库

from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt

之后准备之前的数据

X = np.empty(shape=(100,2))
X[:,0] = np.random.uniform(0,100,size=100) # 生成0-100之间100个随机数
X[:,1] = 0.6*X[:,0]+5 + np.random.normal(0,10,size=100)

最后进行演示

pca = PCA(n_components=2)
pca.fit(X)
pca.components_

其实我们也可以使用真实数据进行演示，下面我们进行真实数据的案例演示

---

首先做前期的准备

from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data
y = digits.target

这里我们使用KNN算法进行演示

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y)  # 分割数据集和测试集

之后得出降维前的准确率

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
%%time
knn_clf.fit(X_train,y_train)
knn_clf.score(X_test,y_test)

运行结果如下

之后我们进行降维，将64维降维2维

pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction= pca.transform(X_train)
X_test_reduction= pca.transform(X_test)
%%time
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
knn_clf.score(X_test_reduction,y_test)

运行结果如下

• pca.transform方法会将原始特征数据投影到PCA的主成分空间中，得到一个新的特征矩阵，其中每一列代表一个主成分，每一行代表一个训练样本。

通常情况下我们在降维的时候保留原始数据总方差的95%

pca = PCA(0.95) # 降维时保留95%的原始数据总方差
pca.fit(X_train)
X_train_reduction= pca.transform(X_train)
X_test_reduction= pca.transform(X_test)

最后得到的准确率为

所以说降维不要太离谱，否则信息损失太多！！！

挑战与创造都是很痛苦的，但是很充实。