LeetCode 139. 单词拆分（动态规划，DFS和BFS解决）

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

public boolean wordBreak(String s, List<String> dict) {
    boolean[] dp = new boolean[s.length() + 1];
    for (int i = 1; i <= s.length(); i++) {
        //枚举k的值
        for (int k = 0; k <= i; k++) {
            //如果往前截取全部字符串，我们直接判断子串[0,i-1]
            //是否存在于字典wordDict中即可
            if (k == i) {
                if (dict.contains(s.substring(0, i))) {
                    dp[i] = true;
                    continue;
                }
            }
            //递推公式
            dp[i] = dp[i - k] && dict.contains(s.substring(i - k, i));
            //如果dp[i]为true，说明前i个字符串结果拆解可以让他的所有子串
            //都存在于字典wordDict中，直接终止内层循环，不用再计算dp[i]了。
            if (dp[i]) {
                break;
            }
        }
    }
    return dp[s.length()];
}

上面代码有一个判断，就是截取的是前面全部字符串的时候要单独判断，其实当截取全部的时候我们只需要判断这个字符串是否存在于字典wordDict中即可，可以让dp[0]为true，dp[0]表示的是空字符串。这样代码会简洁很多，我们来看下

public boolean wordBreak(String s, List<String> dict) {
    boolean[] dp = new boolean[s.length() + 1];
    dp[0] = true;//边界条件
    for (int i = 1; i <= s.length(); i++) {
        for (int j = 0; j < i; j++) {
            dp[i] = dp[j] && dict.contains(s.substring(j, i));
            if (dp[i]) {
                break;
            }
        }
    }
    return dp[s.length()];
}

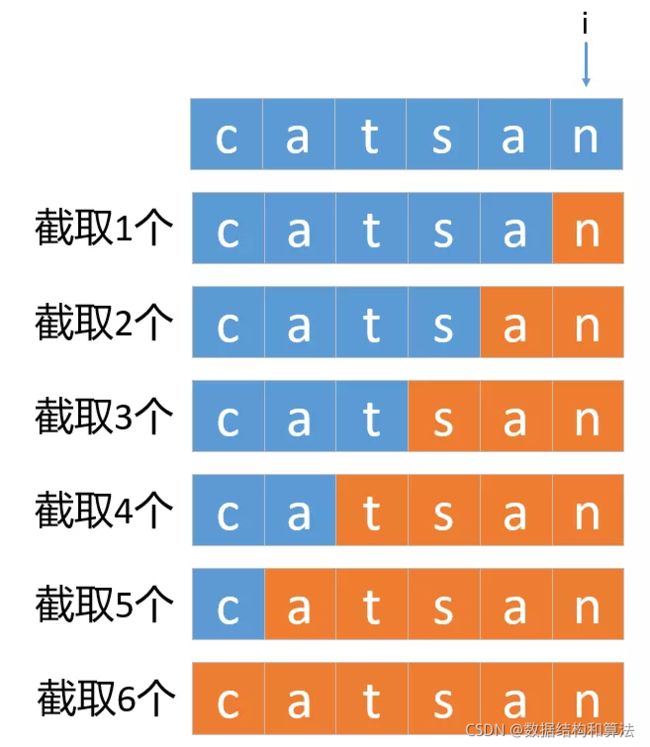
这个和第一种写法不太一样，这个每次截取的方式如下图所示。




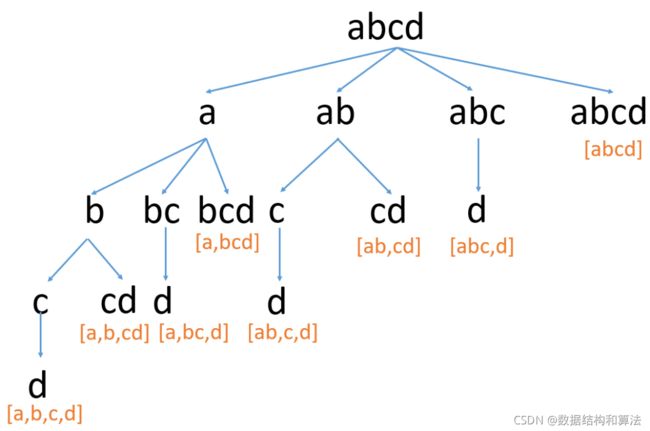
每次截取一个子串，判断他是否存在于字典中，如果不存在于字典中，继续截取更长的子串……如果存在于字典中，然后递归拆分剩下的子串，这是一个递归的过程。上面的执行过程我们可以把它看做是一棵n叉树的DFS遍历，所以大致代码我们可以列出来

public boolean wordBreak(String s, List<String> wordDict) {
    return dfs(s, wordDict);
}

public boolean dfs(String s, List<String> wordDict) {
    if (最终条件，都截取完了，直接返回true)
    return true;
    //开始拆分字符串s
    for (int i = 开始截取的位置; i <= s.length(); i++) {
        //如果截取的子串不在字典中，继续截取更大的子串
        if (!wordDict.contains(截取子串))
            continue;
        //如果截取的子串在字典中，继续剩下的拆分，如果剩下的可以拆分成
        //在字典中出现的单词，直接返回true，如果不能则继续
        //截取更大的子串判断
        if (dfs(s, wordDict))
            return true;
    }
    //如果都不能正确拆分，直接返回false
    return false;
}

上面代码中因为递归必须要有终止条件，通过上面的图我们可以发现，终止条件就是把字符串s中的所有字符都遍历完了，这个时候说明字符串s可以拆分成一些子串，并且这些子串都存在于字典中。我们来看个图

因为是拆分，所以字符串截取的时候不能有重叠，那么[开始截取的位置]实际上就是上次截取位置的下一个，来看下代码。

public boolean wordBreak(String s, List<String> wordDict) {
    return dfs(s, wordDict, 0);
}

//start表示的是从字符串s的哪个位置开始
public boolean dfs(String s, List<String> wordDict, int start) {
    //字符串中的所有字符都遍历完了，也就是到叶子节点了，说明字符串s可以拆分成
    //在字典中出现的单词，直接返回true
    if (start == s.length())
        return true;
    //开始拆分字符串s，
    for (int i = start + 1; i <= s.length(); i++) {
        //如果截取的子串不在字典中，继续截取更大的子串
        if (!wordDict.contains(s.substring(start, i)))
            continue;
        //如果截取的子串在字典中，继续剩下的拆分，如果剩下的可以拆分成
        //在字典中出现的单词，直接返回true，如果不能则继续
        //截取更大的子串判断
        if (dfs(s, wordDict, i))
            return true;
    }
    return false;
}

实际上上面代码运行效率很差，这是因为如果字符串s比较长的话，这里会包含大量的重复计算，我们还用上面的图来看下

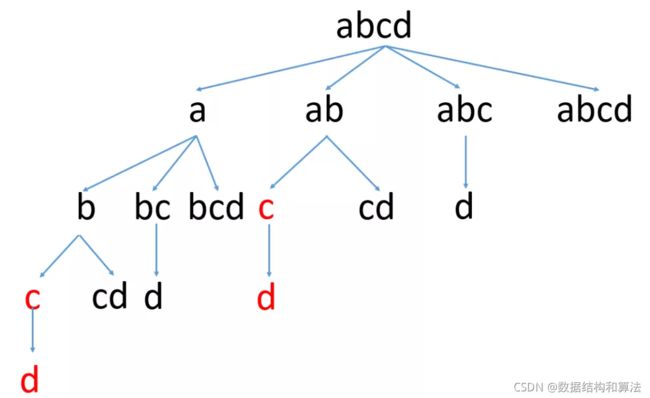
我们看到红色的就是重复计算，这里因为字符串比较短，不是很明显，当字符串比较长的时候，这里的重复计算非常多。我们可以使用一个变量，来记录计算过的位置，如果之前判断过，就不在重复判断，直接跳过即可，代码如下

public boolean wordBreak(String s, List<String> wordDict) {
    return dfs(s, wordDict, new HashSet<>(), 0);
}

//start表示的是从字符串s的哪个位置开始
public boolean dfs(String s, List<String> wordDict, Set<Integer> indexSet, int start) {
    //字符串都拆分完了，返回true
    if (start == s.length())
        return true;
    for (int i = start + 1; i <= s.length(); i++) {
        //如果已经判断过了，就直接跳过，防止重复判断
        if (indexSet.contains(i))
            continue;
        //截取子串，判断是否是在字典中
        if (wordDict.contains(s.substring(start, i))) {
            if (dfs(s, wordDict, indexSet, i))
                return true;
            //标记为已判断过
            indexSet.add(i);
        }
    }
    return false;
}

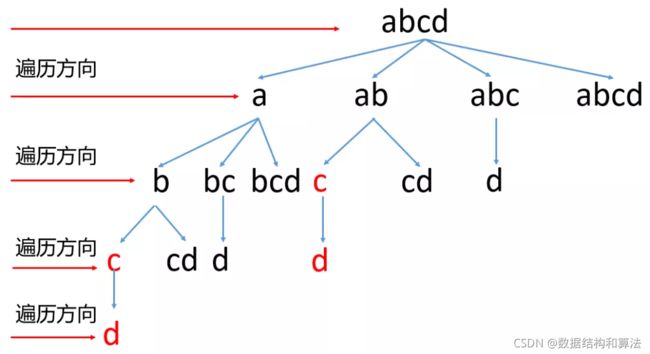
BFS一般不需要递归，只需要使用一个队列记录每一层需要记录的值即可。BFS中在截取的时候，如果截取的子串存在于字典中，我们就要记录截取的位置，到下一层的时候就从这个位置的下一个继续截取，来看下代码。

public boolean wordBreak(String s, List<String> wordDict) {
    //这里为了提高效率，把list转化为set，因为set的查找效率要比list高
    Set<String> setDict = new HashSet<>(wordDict);
    //记录当前层开始遍历字符串s的位置
    Queue<Integer> queue = new LinkedList<>();
    queue.add(0);
    int length = s.length();
    while (!queue.isEmpty()) {
        int index = queue.poll();
        //如果字符串到遍历完了，自己返回true
        if (index == length)
            return true;
        for (int i = index + 1; i <= length; i++) {
            if (setDict.contains(s.substring(index, i))) {
                queue.add(i);
            }
        }
    }
    return false;
}

这种也会出现重复计算的情况，所以这里我们也可以使用一个变量来记录下。

public boolean wordBreak(String s, List<String> wordDict) {
    //这里为了提高效率，把list转化为set，因为set的查找效率要比list高
    Set<String> setDict = new HashSet<>(wordDict);
    //记录当前层开始遍历字符串s的位置
    Queue<Integer> queue = new LinkedList<>();
    queue.add(0);
    int length = s.length();
    //记录访问过的位置，减少重复判断
    boolean[] visited = new boolean[length];
    while (!queue.isEmpty()) {
        int index = queue.poll();
        //如果字符串都遍历完了，直接返回true
        if (index == length)
            return true;
        //如果被访问过，则跳过
        if (visited[index])
            continue;
        //标记为访问过
        visited[index] = true;
        for (int i = index + 1; i <= length; i++) {
            if (setDict.contains(s.substring(index, i))) {
                queue.add(i);
            }
        }
    }
    return false;
}