回归与聚类算法系列④：岭回归

目录

1. 背景

2. 数学模型

3. 特点

4. 应用领域

5. 岭回归与其他正则化方法的比较

6、API

7、代码

8、总结

---

作者介绍：双非本科大三网络工程专业在读，阿里云专家博主，专注于Java领域学习，擅长web应用开发、数据结构和算法，初步涉猎Python人工智能开发。

主页：@逐梦苍穹

回归与聚类算法系列

⭐①：概念简述

⭐②：线性回归

⭐③：欠拟合与过拟合

您的一键三连，是我创作的最大动力

岭回归（Ridge Regression）是线性回归的一种变体，它在专业统计和机器学习领域中应用广泛。岭回归的核心目标是解决线性回归中的过拟合问题，并提高模型的泛化性能。

1. 背景

岭回归最早由统计学家Arthur E. Hoerl和Robert W. Kennard于1970年提出，是为了解决多重共线性（Multicollinearity）问题而诞生的。多重共线性是指在线性回归中，自变量之间存在高度相关性的情况，这会导致模型参数的估计不稳定，降低了模型的解释性能。

2. 数学模型

岭回归与线性回归类似，但在损失函数中引入了L2正则化项，用于惩罚模型参数的大小。

岭回归的数学模型如下所示：

其中：

• yi 是观测数据点（目标变量）。
• xij 是输入特征矩阵的元素，表示第 i 个观测数据点的第 j 个特征。
• β0 和 βj 是模型的参数，需要估计。
• α 是岭回归的正则化参数，也称为正则化强度或惩罚参数。

损失函数的第一部分是最小二乘法的残差平方和，第二部分是L2正则化项。α是超参数，用于控制正则化的强度。较大的α值会导致模型参数趋于收缩，减小过拟合的风险。

3. 特点

• 解决多重共线性：岭回归可以处理自变量之间的高度相关性，使得模型参数估计更稳定。
• 增加模型复杂度：岭回归允许模型更复杂，因为正则化项允许参数取较大的值，但在不引入过拟合的情况下。
• 参数缩减：岭回归的正则化项会使一些参数趋于零，实现了参数缩减（Parameter Shrinkage）。
• 泛化能力提高：通过减小模型的方差，岭回归通常提高了模型在新数据上的泛化能力。

4. 应用领域

• 经济学：用于经济数据建模，以预测经济变量之间的关系。
• 生物统计学：用于基因表达分析和生物信息学领域，以处理高维数据。
• 工程学：用于工程建模和控制系统设计，以改善模型的鲁棒性。
• 金融学：用于资产定价和风险管理，以降低投资组合的风险。

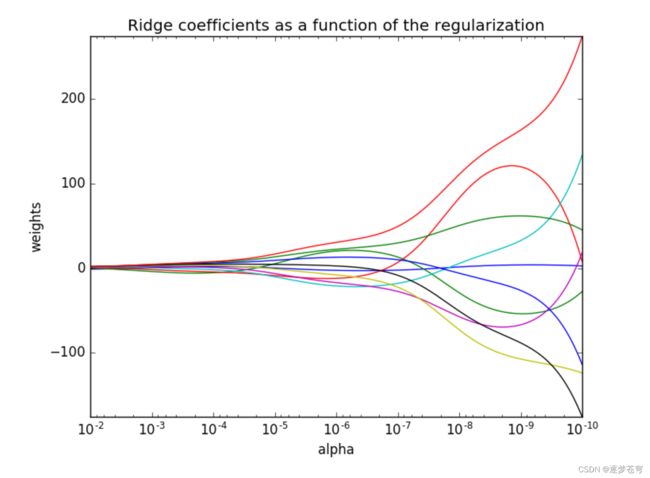
5. 岭回归与其他正则化方法的比较

正则化力度越大，权重系数会越小

正则化力度越小，权重系数会越大

岭回归是一种L2则化方法，与L1正则化方法（如LASSO回归）不同，L1正则化可以导致参数稀疏性。选择哪种方法通常取决于具体问题和数据集的性质。

岭回归、LASSO回归和Elastic Net回归是三种常见的正则化线性回归方法，它们在处理多重共线性和过拟合问题时有不同的特点。下面是这三种方法之间的比较：

1. 岭回归（Ridge Regression）：

• 正则化项： 岭回归使用L2正则化项，即对模型参数的平方和进行惩罚。
• 特点： 岭回归通过约束参数的平方和来控制参数的大小，使得模型参数趋于较小的值，但不会将参数压缩到零。
• 解决的问题： 主要用于解决多重共线性问题和过拟合问题，可以保留所有特征，但对它们的权重进行缩减。
• 稳定性： 对于高度相关的特征，岭回归能够给出相对稳定的参数估计。
• 适用场景： 适用于特征之间存在相关性，但不希望丢弃特征的情况。

2. LASSO回归（Least Absolute Shrinkage and Selection Operator）：

• 正则化项： LASSO回归使用L1正则化项，即对模型参数的绝对值之和进行惩罚。
• 特点： LASSO回归倾向于将不重要的特征的参数压缩到零，从而实现特征选择（Feature Selection）。
• 解决的问题： 同样用于解决多重共线性和过拟合问题，但通常会导致一些特征的系数变为零，从而实现特征选择。
• 稳定性： 在存在高度相关的特征时，LASSO回归可能会随机选择其中一个特征。
• 适用场景： 适用于希望进行特征选择的情况，可以减少模型的复杂度。

3. Elastic Net回归：

• 正则化项： Elastic Net回归结合了L1正则化项和L2正则化项，同时对模型参数的绝对值和平方和进行惩罚。
• 特点： Elastic Net回归综合了岭回归和LASSO回归的优点，可以在解决多重共线性和过拟合问题的同时进行特征选择。
• 解决的问题： 适用于综合考虑多重共线性和特征选择的问题。
• 稳定性： 在存在高度相关的特征时，Elastic Net回归相对稳定，并可以选择一组相关性较高的特征。
• 适用场景： 适用于需要综合考虑多个因素的情况，既希望减少特征数又需要保留相关性高的特征。

选择合适的正则化方法通常取决于具体问题和数据集的性质。如果特征之间存在高度相关性，但不希望进行特征选择，岭回归可能是一个良好的选择。如果需要进行特征选择，LASSO回归或Elastic Net回归可能更合适。不同方法之间的超参数需要进行调优，以获得最佳模型性能。

6、API

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)

    具有l2正则化的线性回归

    alpha:正则化力度，也叫 λ

        λ取值：0~1 1~10

    solver:会根据数据自动选择优化方法

        sag:如果数据集、特征都比较大，选择该随机梯度下降优化

    normalize:数据是否进行标准化

        normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据

    Ridge.coef_:回归权重

    Ridge.intercept_:回归偏置

All last four solvers support both dense and sparse data. However,

only 'sag' supports sparse input when `fit_intercept` is True.

这段话解释了关于使用不同优化方法时对稠密（dense）和稀疏（sparse）数据以及fit_intercept参数的支持情况。

首先，这里提到的四种优化方法是用于岭回归模型的优化方法。它们分别是：

1. auto: 这个选项会根据数据的大小和特征数自动选择最适合的优化方法。
2. sag: 随机平均梯度下降（Stochastic Average Gradient Descent）方法，通常用于处理大型数据集和特征数较多的情况。
3. 其他两种方法未在这段话中详细说明。

然后，这段话指出，这四种优化方法都支持处理稠密和稀疏数据。稠密数据是指数据集中的大多数元素都是非零的，而稀疏数据是指数据集中的大多数元素都是零的。这些优化方法可以适用于两种类型的数据。

有一个例外情况：当设置fit_intercept=True时，只有sag方法支持处理稀疏数据。这是因为当fit_intercept为True时，模型需要估计偏置（intercept），而sag方法是唯一支持在这种情况下使用稀疏输入数据的方法。其他方法在这种情况下可能会导致错误或不稳定的行为。

因此，如果你的数据是稀疏的，并且你需要拟合一个带有偏置的岭回归模型，那么最好选择sag优化方法。如果你使用其他优化方法，并且希望处理稀疏数据，建议在调用岭回归之前使用preprocessing.StandardScaler等方法手动将数据标准化。

Ridge方法相当于SGDRegressor(penalty='l2', loss="squared_loss")。

只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

具有l2正则化的线性回归，可以进行交叉验证

coef_:回归系数

class _BaseRidgeCV(LinearModel):

    def __init__(self, alphas=(0.1, 1.0, 10.0),

                 fit_intercept=True, normalize=False, scoring=None,

                 cv=None, gcv_mode=None,

                 store_cv_values=False):

7、代码

# -*- coding: utf-8 -*-
# @Author:︶ㄣ释然
# @Time: 2023/9/6 10:37
import warnings

import joblib
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

'''
sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
    具有l2正则化的线性回归
    alpha:正则化力度，也叫 λ
        λ取值：0~1 1~10
    solver:会根据数据自动选择优化方法
        sag:如果数据集、特征都比较大，选择该随机梯度下降优化
    normalize:数据是否进行标准化
        normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
    Ridge.coef_:回归权重
    Ridge.intercept_:回归偏置
'''
def ridge():
    """
    岭回归对波士顿房价进行预测
    :return:
    """
    # 1）获取数据
    boston = load_boston()
    print("特征数量：\n", boston.data.shape)

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)

    # 3）标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）预估器
    estimator = Ridge(alpha=0.5, max_iter=10000)
    estimator.fit(x_train, y_train)

    # 保存模型
    joblib.dump(estimator, "my_ridge.pkl")
    # 加载模型
    # estimator = joblib.load("my_ridge.pkl")

    # 5）得出模型
    print("岭回归-权重系数为：\n", estimator.coef_)
    print("岭回归-偏置为：\n", estimator.intercept_)

    # 6）模型评估
    y_predict = estimator.predict(x_test)
    print("预测房价：\n", y_predict)
    error = mean_squared_error(y_test, y_predict)
    print("岭回归-均方误差为：\n", error)


if __name__ == '__main__':
    warnings.filterwarnings("ignore")
    ridge()

8、总结

总之，岭回归是一种强大的工具，用于改善线性回归模型的性能，并处理多重共线性问题。它在各种领域中都有着广泛的应用，特别是在需要处理高维数据或自变量相关性较强的情况下，岭回归可以提供可靠的模型估计。