《probabilistic robotics》学习笔记——卡尔曼滤波

机器人系列文章目录

第一章 ubuntu16.04系统及相关软件安装
第二章 Linux操作系统入门笔记
第三章 ROS系统架构及程序编写过程
第四章 《probabilistic robotics》学习笔记

---

---

chpt1 绪论

probabilistic robotics核心是estimating state from sensor data。用概率理论的运算去明确地表示机器人感知和行为的不确定性。即，不再只依赖可能出现情况的单一的“最好推测best guess”，而是用概率算法来表示在整个推测空间的概率分布信息。

eg1：Markov localization
eg2：coastal navigation

chpt2 递归状态估计

2.2 概率论概念

全概率公式p16
贝叶斯公式
先验概率（prior probability）：p（x）
后验概率（posterior probability）：p（x|y）
多条件贝叶斯概率
期望
熵（entropy）p18

注：公式参考：https://www.jianshu.com/p/37daf3b83ffc

2.3 机器人环境交互

2.3.1 state
state用于表示环境
pose包含location和orientation
1.位置（x,y,z）
机器人中二维只用到x，y。
坐标系为右手系：朝前的方向为x轴；各轴正方向同样为右手系。

2.欧拉角（roll,pitch,yaw）
翻滚角，俯仰角，偏航角。只用到yaw。
3.Quaternion(四元数)q=w+xi+yj+zk( w 是实数，x,y,z是虚数)=[[w,v]] (v=(x,y,z)是四维空间的矢量，w是标量)底层代码需要。转换为欧拉角时，只有yaw有值。
4.速度：线速度、角速度。只需要两个参数x和theta。

2.3.2 environment interaction
measurement利用传感器获取环境状态
Control actions

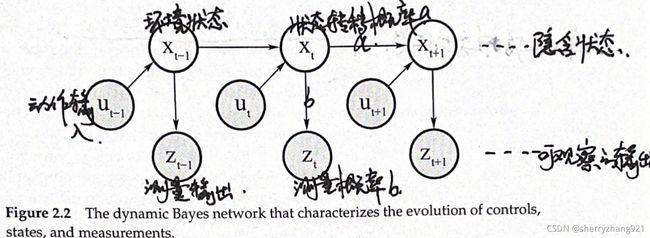
2.3.3 probabilistic generative laws
1.状态转移概率：
Xt只与Xt-1和ut有关：p（xt|xt-1，ut）
2.测量概率：
Zt只与Xt有关：p（zt|xt）

2.3.4 Belief Distribution

反映了机器人有关环境状态的内部信息。由坐标数据推导出位姿。
假设机器人通过条件概率分布表示belief，belief distribution为每一个可能的假设分配一个概率（概率密度值）。置信度分布是以可以获得的数据为条件的关于状态变量的后验概率，用bel(xt)表示，xt是state variable状态变量。这个后验是时刻t下状态xt的概率分布，以过去所有的变量x1:t和所有过去的控制u1:t为条件：
**bel(xt)=p(xt|z1:t,u1:t）**打喷嚏时避免向着其他的人
默认的置信度是综合了测量zt后得到的，但是在刚刚执行ut之后，综合zt之前计算后验是十分有用的，这样的后验就可以表示为：
bel (xt)=p(xt|z1:t−1,u1:t)
在概率滤波的框架下此概率经常被称为预测（prediction），bel (xt)是基于以前状态的后验，在综合时刻t的测量之前预测了时刻t的状态，由bel (xt)计算bel(xt)称为修正(correction)或测量更新（measurement update）

2.4 贝叶斯滤波算法

用于估计环境和机器人状态。
给出所有过去的传感器测量和控制数据，计算xt状态的后验，即bel。

推导过程：略
推导假设世界是马尔科夫的，即状态是完整的

具体实现条件：
1.初始置信initial belief：p（x0）
2.测量概率measurement probability：p（zt|xt）
3.状态转移概率state transition probability：p（xt|ut，xt-1）

2.4.4 马尔科夫假设
Markov assumption or complete state assumption（状态完备假设）
过去和未来的数据独立
一般经验法则：定义状态xt时要excise care（以便unmodeled state variables有接近随机的影响）

chpt3 高斯滤波器

是一类递归状态的估计。是贝叶斯滤波器在连续空间中的实现。
基本思想：belief置信由多元正态分布表示。
其中高斯函数单峰unimodal；高斯分布的均值和协方差表示称为矩参数moments parameterization

3.2 卡尔曼滤波器

线性高斯
用于连续状态的belief计算，由矩参数表示。
若如下三个性质不变，且满足贝叶斯滤波器的马尔科夫假设，则后验为高斯：
状态转移概率是带有随机高斯噪声的参数的线性函数；测量概率与带有高斯噪声的自变量呈线性关系；初始置信度是正态分布的。
KF 表示均值为μ_t、方差为 sigma_t的在时刻 t 的置信度 bel(x,) 。 KF 的输入就是 t - 1 时刻的置信度,其均值和
方差分别用μ_t-1 和 sigma_t-1 表示。为了更新这些参数, KF 需要控制向量 u_t和测量向量 z_t。输出的是时刻 t 的置信度,均值为μ_t、方差为 sigma_t.
以下版权：https://blog.csdn.net/weixin_44580210/article/details/90417331
A ：状态转移系数矩阵，n×n
B ：可选的控制输入的增益矩阵
R ：过程激励噪声的协方差矩阵
C ：量测系数矩阵，m×n
Q ：测量噪声协方差矩阵

3.3 扩展的卡尔曼滤波

非线性高斯系统
放宽了一个假设：线性化假设。这里假设状态转移概率和测量概率分别由非线性函数控制。
为线性化：一阶泰勒展开，从状态转移方程和测量方程中线性化得到两个雅可比矩阵：G_t,H_t

3.4 无迹卡尔曼滤波

线性化的另一种方法：通过使用加权统计线性回归过程实现随机线性化。
即无迹变换（unscented transform）：主要通过n个在先验分布中采集的点（我们把它们叫sigma points）的线性回归来线性化随机变量的非线性函数。
对比：由于我们考虑的是随机变量的扩展，所以这种UKF线性化要比泰勒级数线性化（EKF所使用的策略）更准确；UKF能有效地克服EKF估计精度低、稳定性差的问题，因为不用忽略高阶项，所以对于非线性分布统计量的计算精度高，能有效地克服EKF估计精度低、稳定性差的问题。
————————————————
版权文链接：https://blog.csdn.net/weixin_42905141/article/details/99710297

算法：分为预测和更新，见上文后半部分。

3.5 信息滤波器The Information Filter

信息滤波使用 信息矩阵和信息矢量 进行迭代，它是kalman滤波的信息格式，利用矩阵的稀疏性优化效率