卡尔曼滤波

$声明：本笔记仅仅为本人学习卡尔曼滤波时所总结，仅供交流学习，侵删。$

1. 定义输入

输入：一个符合高斯分布的已知状态量$x_{k-1}$，且该高斯分布的协方差矩阵为${\mathbf{P}}_{\mathbf{k}-1}$

2. 输入状态量到中间预测状态量

接下来，我们需要根据已知状态量来预测下一个步长的状态$x_k$，我们需要状态转移矩阵${\mathbf{F}}_{\mathbf{k}}$和控制矩阵${\mathbf{B}}_{\mathbf{k}}$来预测我们的下一个状态$x_k$，并且需要规定我们的控制向量$u_k$，相关的表达式如下：
$$x_k={\mathbf{F}}_{\mathbf{k}}{\mathbf{x}}_{\mathbf{k}-1}+{\mathbf{B}}_{\mathbf{k}}{\mathbf{u}}_{\mathbf{k}}\text{\hspace{1em}(1)}$$
因为我们对每个点都进行了状态转移的预测，因此协方差矩阵也需要跟着转换，结果为：
$${\mathbf{P}}_{\mathbf{k}}={\mathbf{F}}_{\mathbf{k}}{\mathbf{P}}_{\mathbf{k}-1}{\mathbf{F}}_{\mathbf{k}}^{\mathbf{T}}\text{\hspace{1em}(2)}$$
证明如下：已知协方差矩阵$\text{Var}[\mathbf{x}]=\text{Cov}[\mathbf{x},\mathbf{x}]=\mathbf{\Sigma }$，那么我们可以得到：
一个已知前提：$E\left[Fx\right]=FE[x]$,证明参考协方差矩阵的简单介绍，因此：
$$\begin{array}{rl}\text{Var}[\mathbf{Fx}]& =\text{Cov}[\text{F}x,\text{F}x]\\ & =\text{E}\{(Fx-E[Fx])(Fx-E[Fx]{)}^T\}\\ & =\text{E}\{(Fx-FE[x])(Fx-FE[x]{)}^T\}\\ & =\text{E}\{F(x-E[x])(x-E[x]{)}^T{F}^T\}\\ & =F\text{E}\{(x-E[x])(x-E[x]{)}^T\}{F}^T\\ & =F\Sigma F^T\end{array}\text{\hspace{1em}(3)}$$

3. 考虑外部动力和噪声

$x_{k-1}$中的每个点移动到一个符合协方差的${\text{Q}}_k$高斯分布里（也就是蓝色的高斯分布移动到紫色高斯分布的位置），或者说，把这些不确定的外部因素描述为协方差为的高斯噪声${\text{Q}}_k$，具体根据预测的传感器噪声来定（比如imu或者轮速计）：

对${\text{Q}}_k$ 简单叠加，可以拿到扩展的协方差，这样就得到了预测步骤的完整表达式：
$$\begin{array}{rl}& x_k={\mathbf{F}}_{\mathbf{k}}{\mathbf{x}}_{\mathbf{k}-1}+{\mathbf{B}}_{\mathbf{k}}{\mathbf{u}}_{\mathbf{k}}\\ & {\mathbf{P}}_{\mathbf{k}}={\mathbf{F}}_{\mathbf{k}}{\mathbf{P}}_{\mathbf{k}-1}{\mathbf{F}}_{\mathbf{k}}^{\mathbf{T}}+{\text{Q}}_{\mathbf{k}}\end{array}\text{\hspace{1em}(4)}$$

4. 高维高斯分布叠加

上述表达就是关于数学模型的预测方法，但是完成这些是不够的，因为我们知道预测得到的是一个高斯分布，且仅仅只是经过我们一次预测得到的结果，如果我们将更多已知的信息加入到数学模型中，那么我们将得到更加准确的或者说更加符合实际的结果，因此我们结合许多应用卡尔曼滤波的项目中具有大量传感器获取的测量值的情况，并且这些测量值因为有着精度和环境噪声等的影响，我们将它们也当做是符合高斯分布的数学模型，而两个高斯分布我们可以通俗地理解成以下图形：

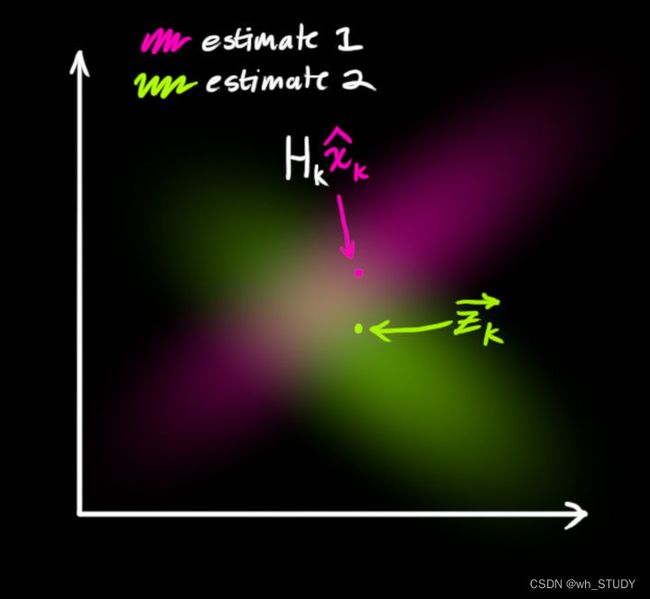
为了得到更加准确的结果，我们认为两个高斯分布重叠的部分比它们原来两个中的任何一个高斯分布都更加符合实际（最优卡尔曼增益相关证明参考卡尔曼滤波（Kalman Filter）原理与公式推导），因此如何融合两个高斯分布呢？

我们从简单的一维高斯分布来看：
$$\begin{array}{rl}& N(x,{\mu }_0,{\sigma }_0)\ast N(x,{\mu }_1,{\sigma }_1)\\ & =\frac{1}{{\sigma }_0\sqrt{2\pi }}{e}^{-\frac{(x-{\mu }_0{)}^2}{2{\sigma }_0^2}}\cdot \frac{1}{{\sigma }_1\sqrt{2\pi }}{e}^{-\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}}\\ & =\frac{1}{\sqrt{2\pi }}\frac{1}{\sqrt{2\pi }{\sigma }_0{\sigma }_1}{e}^{-\frac{({\sigma }_0^2+{\sigma }_1^2)x^2-2({\mu }_0{\sigma }_1^2+{\mu }_1{\sigma }_0^2)x+{\sigma }_1^2{\mu }_0^2+{\sigma }_0^2{\mu }_1^2}{2({\sigma }_0{\sigma }_1{)}^2}}\\ & =\frac{1}{\sqrt{2\pi }}\frac{1}{\sqrt{2\pi }{\sigma }_0{\sigma }_1}{e}^{-\frac{{\left(x-\frac{{\mu }_0{\sigma }_1^2+{\mu }_1{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}\right)}^2}{2{\left(\frac{{\sigma }_0{\sigma }_1}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}\right)}^2}+\underset{常数\lambda =\frac{({\mu }_0-{\mu }_1{)}^2}{2({\sigma }_0^2+{\sigma }_1^2)}}{\frac{\frac{{\sigma }_1^2{\mu }_0^2+{\sigma }_0^2{\mu }_1^2}{{\sigma }_0^2+{\sigma }_1^2}-{\left(\frac{{\mu }_0{\sigma }_1^2+{\mu }_1{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}\right)}^2}{2{\left(\frac{{\sigma }_0{\sigma }_1}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}\right)}^2}}}\\ & =C\frac{1}{\sqrt{2\pi }\frac{{\sigma }_0{\sigma }_1}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}}{e}^{-\frac{{\left(x-\frac{{\mu }_0{\sigma }_1^2+{\mu }_1{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}\right)}^2}{2{\left(\frac{{\sigma }_0{\sigma }_1}{\sqrt{{\sigma }_0^2+{\sigma }_1^2}}\right)}^2}}\\ & 其中，C代表常数项，从而有\\ & {\mu }^{\prime }=\frac{{\mu }_0{\sigma }_1^2+{\mu }_1{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}={\mu }_0+({\mu }_1-{\mu }_0)\frac{{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}\\ & {\sigma }^{\prime 2}=\frac{{\sigma }_0^2{\sigma }_1^2}{{\sigma }_0^2+{\sigma }_1^2}={\sigma }_0^2-{\sigma }_0^2\frac{{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}\end{array}\text{\hspace{1em}(5)}$$
令$k=\frac{{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}$,则：
$$\begin{array}{rl}& {\mu }^{\prime }={\mu }_0+k({\mu }_1-{\mu }_0)\\ & {\sigma }^{\prime 2}={\sigma }_0^2-k{\sigma }_0^2\end{array}\text{\hspace{1em}(6)}$$
如果是一个多维矩阵呢？我们将(6)表示为矩阵形式。$\Sigma$表示协方差矩阵， $\mu$表示平均向量：
$$K={\Sigma }_0{\left({\Sigma }_0+{\Sigma }_1\right)}^{-1}\text{\hspace{1em}(7)}$$

$$\begin{array}{rl}& {\mu }^{\prime }={\mu }_0+K\left({\mu }_1-{\mu }_0\right)\\ & {\Sigma }^{\prime }={\Sigma }_0-K{\Sigma }_0\end{array}\text{\hspace{1em}(8)}$$

5. 从状态域转换为观测域

有了以上的基础，我们还需要将预测值转化为与测量值同维度的形式，即预测值在测量维度上的表达可以通过相信变换矩阵$H_k$相当于状态域通过$H_k$转换到观测域。

${\mu }_{measured}=H_k\ast x_k$

${\Sigma }_{measured}=H_k{\text{P}}_k{H}_k^T$

进而，我们知道：

观测域上的预测值：$\left({\mu }_0,{\Sigma }_0\right)=\left(H_k{x}_k,H_k{\text{P}}_k{H}_k^T\right)$

实际的测量值：$\left({\mu }_1,{\Sigma }_1\right)=\left(z_k^{\prime },R_k\right)$

6. 生成新的状态作为下次迭代的输入

将上述两个多维高斯分布代入(8)中，得到它们的重叠区域：
$$\begin{gathered} H_k{x}_k^{\prime }=H_k+K\left(z_k-H_k{x}_k\right) \\ {H}_k{\text{P}}_k^{\prime }{H}_k^T=H_k{\text{P}}_k{H}_k^T-K{H}_k{\text{P}}_k{H}_k^T\text{\hspace{1em}(9)} \end{gathered}$$
从(7)中我们可以得到卡尔曼增益为：
$$K=H_k{\text{P}}_k{H}_k^T{\left(H_k{\text{P}}_k{H}_k^T+R_k\right)}^{-1}\text{\hspace{1em}(10)}$$
但是上述式子(9)左侧表示的并不是我们需要的状态估计值$x_k^{\prime }$，因此在(9)的第一个式子左右两边各左乘一个$H_k^{-1}$,第二个式子左右两边先左乘一个$H_k^{-1}$然后右乘一个${H_k^T}^{-1}$（可调换顺序），这样我们将会得到如下结果：
$$\begin{gathered} x_k^{\prime }=x_k+K^{\prime }\left(z_k-H_k{x}_k\right) \\ {\text{P}}_k^{\prime }={\text{P}}_k-K^{\prime }{H}_k{\text{P}}_k=\left(E-K^{\prime }{H}_k\right){\text{P}}_k\text{\hspace{1em}(11)} \end{gathered}$$

$$K^{\prime }={\text{P}}_k{H}_k^T{\left(H_k{\text{P}}_k{H}_k^T+R_k\right)}^{-1}\text{\hspace{1em}(12)}$$

7. 整体流程

所有输入量、中间变量、输出量的关系以及输出量的迭代在下图中被表达出来：

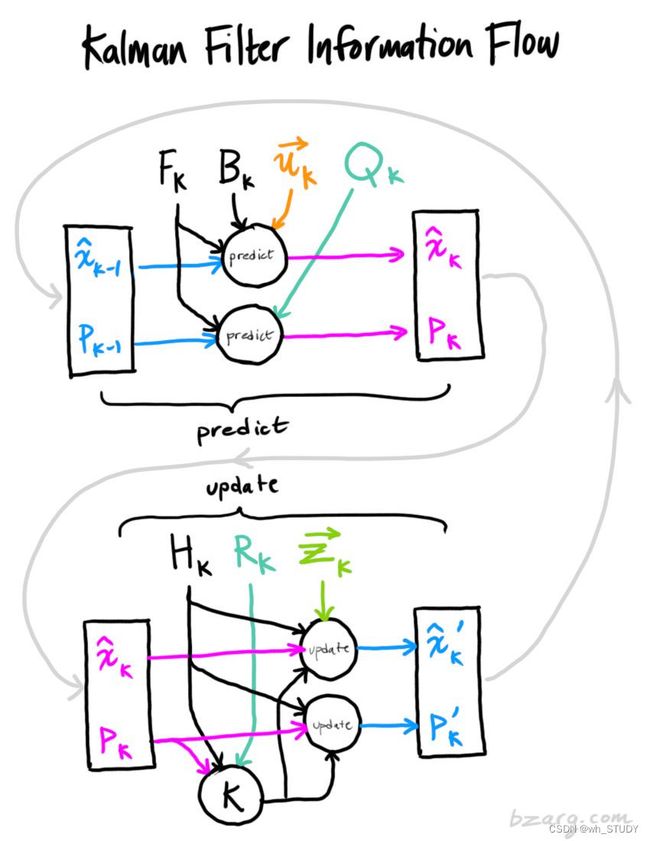
一个简化的流程被表达为：

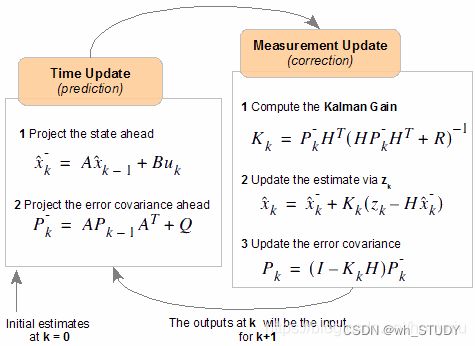
参考资料：

1.卡尔曼滤波更加详细资料