C语言实现单链表
文章目录
- 前言
- 链表
-
- 单链表
- 节点的创建
- 单链表的读取
- 单链表节点的插入
- 单链表节点的删除
- 单链表整表的创建
- 单链表整表的删除
- 单链表结构和顺序表结构的优缺点
前言
单链表可以说是数据结构的基础,学懂了单链表对后面学的栈,队列都有帮助,甚至学好了单链表,后续的树结构学的也会轻松一点,所以链表这里一定要刷题,看书,看视频。
链表
顺序表的缺陷:
1、空间不够,需要扩容。扩容(尤其是异地扩容)是有一定代价的。其次还可能存在一定空间浪费。
2、头部或者中部插入删除,需要挪动数据,效率低下。
根据上述两个缺陷我们就提出了解决方案:
1、按需申请释放
2、不要挪动数据
所以人们就创造了线性表的链式存储结构,又称其为链表:
概念:链表是一种物理存储结构上可能是非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表
中的指针链接次序实现的 。
链表是由一个又一个节点组成的,而节点又包含了两部分,分别是数据域和指针域。
数据域顾名思义就是存放数据的,而指针域的作用是确定下一个节点空间在计算机中的位置,因为链表的空间在计算机中可能是非连续的,所以每一个指针域就要确定下一个节点的位置。就好像你上了大学或工作以后可能不和家长住在一起,而你的父母可能在你走后出去旅游甚至搬家,这个时候你就需要一部手机和他们联系来确定他们所在的位置,否则在你放假想回家的时候会找不到家的位置。
单链表
已知有n个节点链接成一个链表,而每个节点中只包含了一个指针域,这样的链表我们称其为单链表。
人们对其结构描述如下图:

这里就是一个个节点组成了单链表,这里可以看到在逻辑结构上链表是连续的,但实际在计算机存储中不一定是连续的。
首先链表的第一个节点叫做头结点,这个节点的数据域不需要存储任何数据,头结点的作用是指向第一个有效节点,因为链表在计算机中开辟的空间可能不连续,所以需要一个指针去确定链表开辟的空间地址。
假设你全家就是一个链表,你爸是第一个有效节点,你妈是第二个有效节点,而你是第三个有效节点,而这时候有人(头结点)要找你,但是他没有你的地址,但是他有你爸的地址,那么他会先找到你爸,但你爸也没有你的地址,就会对这个人(头结点)说我只有我老婆的地址,你去问问我老婆吧,这时候头结点就会去访问第二个有效节点,也就是你的妈妈,而你的妈妈正好有你的地址,就把你的地址告诉了头结点,这时候就可以找到你了。如下图所示:
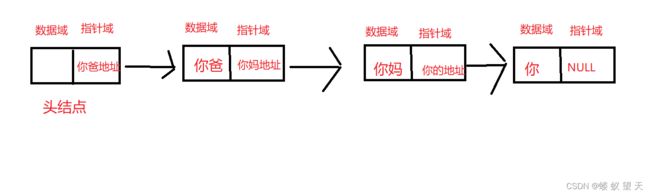
这里可以看出,若一个链表的头结点的指针域指向了空,那么这就是一个空链表,若链表的一个非头结点的指针域指向了空,那么这个节点就是尾结点。
节点的创建
这里节点的数据域就先以整形来举例。
typedef struct Node
{
int data;//数据域,用来存放数据
struct Node* next;//指针域,用来存放下个节点的地址
}Node ,*LinkList;
Node等价于struct Node,而LinkList则等价于struct Node *,在学数据结构的时候我们会经常用typedef来重命名,这样便于代码的简洁性。
单链表的读取
int GetElem(LinkList L, int x, int* e)
{
int j;
LinkList p;//声明一个节点p
p = L->next;//让p指向单链表的第一个有效节点,因为L是头结点,而头结点的指针域存放了第一个有效节点的地址
j = 1;//j作为计数器
while (p && j < x)//若p为空或者j比x大了,那么退出循环
{
p = p->next;//让p指向下一个节点
j++;
}
if (!p || j > x)//第x个数据不存在
{
printf("数据不存在");
return 0;
}
*e = p->data;//x个数据存在
return 1;
}
这里要说的就是首先让p指向了第一个有效节点,因为头节点的指针域存放了第一个有效节点的地址,所以直接让p指针指向L->next就好。
下一个要说的就是让p不断指向下一个节点,因为开头已经让p等价于第一个有效节点了,所以直接让p等于p->next就好,
如下图所示:
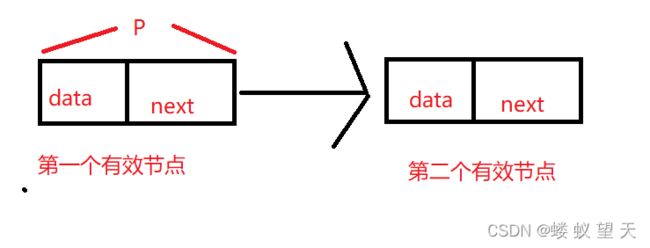
p现在就是第一个有效节点,p->next就有第二个有效节点的地址,所以p=p->next就可以让p等价于第二个有效节点。
单链表节点的插入
其实链表相对于顺序表的优势也在这里,链表插入一个数据的时间复杂度要比顺序表好太多。
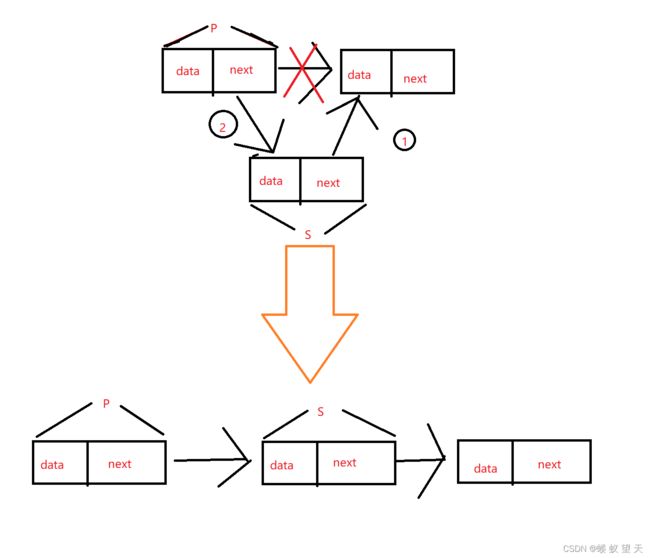
如上图所示,将一个数据插入链表,首先要创建一个节点,之后把数据放在节点的数据域中,第一步将新创建的节点的指针域指向后一位节点,第二步让前一位节点的指针域指向新创建的节点,最后构成一个新的链表。
代码执行如下图:
int ListInsert(LinkList* L, int i, int e)//i代表要将新的节点插入第i个节点后面
{
int j;
LinkList p, s;
p = *L;
j = 1;
while (p && j < i)//寻找第i个节点
{
p = p->next;
j++;
}
if (!p || j > i)//第i个元素不存在
{
return 0;
}
s = (LinkList)malloc(sizeof(Node));//创造一个新的节点
s->data = e;//将新的数据赋值给新节点的数据域
s->next = p->next;//新节点指向插入位置的后一个节点
p->next = s;//第i个节点指向新的节点
return 1;
}
这里有一个知识点注意,我们最开始用typedef对struct Node * 重命名为LinList,而这里我们函数的形参却是LinkList *L,也就是说我们的形参是一个二级指针,那形参设为一级指针行不行?答案肯定是不行的。这里我们就要引出一个经典的例子了:

如上图所示,这个例子大家肯定不陌生,几乎所有人在学C语言指针的时候都会看到这个例子,要通过函数去交换连个整数的值,那么就要就交换这个整数的地址,而同样,我们在数据结构中操作的链表的节点本身就是一个结构体指针,所以我们要去对这个链表做出改变就要从他们的地址入手,我们知道,从整数的地址入手要用到整形指针,而对结构体指针的地址入手,就要用到结构体指针的指针,也就是二级指针(没学好指针的小伙伴一定要赶紧补,C语言数据结构这里就是指针指来指去)。这里如果形参使用一级指针,很容易出bug,而这一句代码p = *L;也是把L的地址给了p,因为L是二级指针,对其一层解引用就是拿到了它的地址,这样p就可以对链表的本体进行操作了。后续对链表的操作,函数的形参几乎都要用到二级指针。
还要说一下这两句代码:
s->next = p->next;//新节点指向插入位置的后一个节点
p->next = s;//第i个节点指向新的节点
这两句代码的顺序是不能颠倒的,若先p->next=s;那么就会失去插入位置后一个节点的的地址,那么链表到了新的节点这里就断掉了。
单链表节点的删除
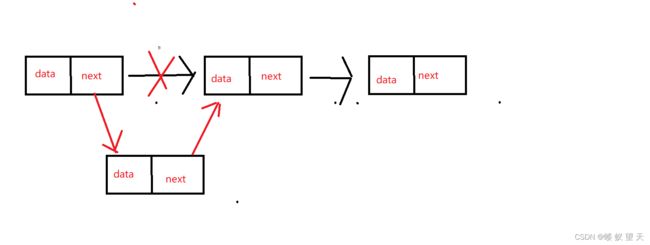
这里也是链表相比于顺序表的一个优势,顺序表若删除一个元素是比较复杂的(尾元素除外),但链表删除节点就很简单。其操作也要比节点的插入简单很多。

如上图所示我们只需要让p的指针域指向q的下一个节点,然后用free释放q就可以了。
代码实现如下:
int ListDelete(LinkList* L, int i, int* e)//删除链表中第i个节点,用e返回第i个节点的数据
{
int j;
LinkList p, q;
p = *L;
j = 1;
while (p->next && j < i)//遍历寻找第i个节点
{
p = p->next;
j++;
}
if (!(p->next) || j > i)//第i个节点不存在
return 0;
q = p->next;//将第i个节点给q
p->next = p->next->next;//让第i个节点的前一个节点指向第i个节点的后一个节点
*e = q->data;//将第i个节点的数据给e
free(q);//让系统回收第i个节点,并释放其空间
return 1;
}
单链表整表的创建
这里我们就直接上代码了:
void CreateListHead(LinkList* L, int n)
{
LinkList p;
int i;
srand(time(0));//初始化随机数种子
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
for (i = 0; i < n; i++)
{
p = (LinkList)malloc(sizeof(Node));//声称新节点
p->data = rand() % 100 + 1;//随机生成100以内的数字
p->next = (*L)->next;
(*L)->next = p;//插入到表头
}
}
这里我们用的创建链表的方法是头插法
如上图所示,每一次都将新的节点插入到头结点之后。
另外还以一种尾插法来创建一整个链表:尾插法
void CreateListTail(LinkList* L, int n)
{
LinkList p, r;
int i;
srand(time(0));
*L = (LinkList)malloc(sizeof(Node));//L代表链表的头结点
r = *L;//r负责指向尾部
for (i = 0; i < n; i++)
{
p = (LinkList)malloc(sizeof(Node));//创造节点
p->data = rand() % 100 + 1;//生成随机数
r->next = p;//将表尾终端的指针指向新节点
r - p;//将当前新节点定义为表尾终端节点
}
r->next = NULL;//表示链表结束
}
单链表整表的删除
单链表整表的的删除就需要对每一个节点进行free。
int ClearList(LinkList* L)
{
LinkList p, q;
p = (*L)->next;//p指向第一个有效节点
while (p)//是否到了链表结尾
{
q = p->next;
free(p);//不断释放空间
p = q;
}
(*L)->next = NULL;//头结点指针域为NULL
return 1;
}
这就是对整条链表的删除。
单链表结构和顺序表结构的优缺点
在存储分配方式上:
顺序存储结构用一段连续存储单元依次存储线性表的数据元素
单链表采用链式存储结构,用一组任意存储单元存放线性表的元素
在空间性能上:
顺序存储结构需要预分配存储空间,分大了会浪费内存,分小了容易发生溢出。
单链表不需要分配存储空间,只要有就可以分配,元素个数也不受限制。
在时间性能上:
顺序表为O(1)
单链表O(n)
插入和删除
顺序表O(n)
单链表O(1)
综上所述:
若需要频繁的查找,很少进行插入和删除操作,适合采用顺序表。
当要存储元素个数变化较大或者根本不知道有多大时,适合采用链表。
最后制作不易,期待你的三连,若有错误,欢迎私信指出。
