一元函数微分学
文章目录
- 一 单调与极值
-
- 1.1 单调性
- 1.2 极值点
- 1.3 判断步骤
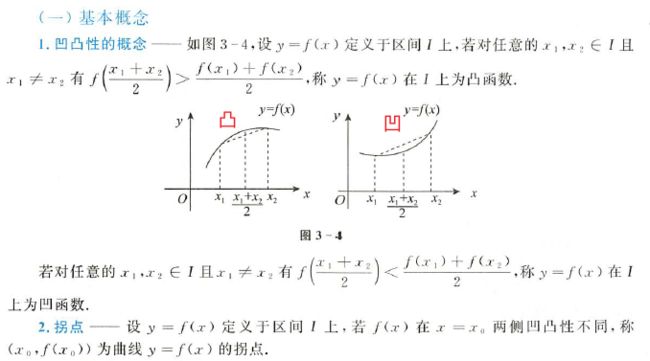
- 二 凹凸性
-
- 2.1 定义
- 2.2 判别法
- 三 渐近线
-
- 3.1 水平渐近线
- 3.2 铅直渐近线
- 3.3 斜渐近线
- 3.4 求法
- 四 弧微分与曲率
- 五 基础例题
-
- 点比较
- 渐近线
- 根与零点
- 不等式证明
一 单调与极值
1.1 单调性
y = f(x) 在D上有定义。x1,x2∈D且x1
- 严格增函数:f(x1) < f(x2)
- 严格减函数:f(x1) > f(x2)
单调性判别法
注解 (增加不一定可导,不可导则导数不存在)
1.2 极值点
定义
x0为f(x)的极大值点:x = x0 处左右去心邻域函数值
x0为f(x)的极小值点:x = x0 处左右去心邻域函数值 >f(x0)
结论1
- f(x)在x=a处取极值,则该点导数为0 或 不存在,反之不对
- f(x)可导且在x=a处取极值则f’(a)=0
- 极值是定义在邻域上的,因此端点不能说极值
- 若连续函数在[a,b]上有唯一极值点,则必为最值(结合图像)
1.3 判断步骤
费马引理:如果函数f(x)在x处可导,且在x处取得极值,那么f’(x0) = 0
步骤:(注意泰勒公式的使用条件f(k)(x)=0)
(命题点) 确定定义域D—求出f’x,求出f(x)的驻点和不可导点—利用判别法判断这些点是否为极值点—利用奇偶性辅助判断—或利用数形结合看图形
驻点:一阶导数=0 (极值点处导数=0,但导数=0处不一定是极值点;即极值点处为驻点或不可导点[尖点],但驻点不一定是极值点)
第一充分条件(有时f’是否变号不好判断)
设 f ( x 0 ) = 0 f\left(x_{0}\right)=0 f(x0)=0 (或 f ( x ) {f(x)} f(x) 在 x 0 x_{0} x0 处连续),且在 x 0 x_{0} x0 的某去心邻域 U ( x 0 , δ ) U\left(x_{0}, \delta\right) U(x0,δ)内可导
(1) 若 x ∈ ( x 0 − δ , x 0 ) x \in\left(x_{0}-\delta, x_{0}\right) x∈(x0−δ,x0)时, f ′ ( x ) > 0 f^{\prime}(x)>0 f′(x)>0,而 x ∈ ( x 0 , x 0 + δ ) x \in\left(x_{0}, x_{0}+\delta\right) x∈(x0,x0+δ)时, f ′ ( x ) < 0 f^{\prime}(x)<0 f′(x)<0,则 f ( x ) {f(x)} f(x)在 x 0 x_{0} x0处取得极大值;
(2) 若 x ∈ ( x 0 − δ , x 0 ) x \in\left(x_{0}-\delta, x_{0}\right) x∈(x0−δ,x0)时, f ′ ( x ) < 0 f^{\prime}(x)<0 f′(x)<0,而 x ∈ ( x 0 , x 0 + δ ) x \in\left(x_{0}, x_{0}+\delta\right) x∈(x0,x0+δ)时, f ′ ( x ) > 0 f^{\prime}(x)>0 f′(x)>0,则 f ( x ) {f(x)} f(x)在$ x_{0} 处取得极小值 ; ( 3 ) 若 处取得极小值; (3) 若 处取得极小值;(3)若 x \in \dot{U} \left(x_{0}, \delta\right) $ 时, f ′ ( x ) f^{\prime}(x) f′(x) 不变号,则 f ( x ) {f(x)} f(x)在 x 0 x_{0} x0 处没有极值
第二充分条件
设 f ( x ) {f(x)} f(x)在 x 0 x_{0} x0处二阶可导,且 f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) ≠ 0 f^{\prime}\left(x_{0}\right)=0, f^{\prime \prime}\left(x_{0}\right) \neq0 f′(x0)=0,f′′(x0)=0,则
(1) 当 f ′ ′ ( x 0 ) < 0 , f ( x ) f^{\prime \prime}\left(x_{0}\right)<0, {f(x)} f′′(x0)<0,f(x)在 x 0 x_{0} x0处取极大值.
(2) 当 f ′ ′ ( x 0 ) > 0 , f ( x ) f^{\prime \prime}\left(x_{0}\right)>0, {f(x)} f′′(x0)>0,f(x)在 x 0 x_{0} x0处取极小值.
泰勒公式判别法
设 f ( x ) {f(x)} f(x)在 x 0 x_{0} x0处 n ( n ≥ 2 ) n(n \geq2) n(n≥2)阶可导,且 f ′ ( x 0 ) = f ′ ′ ( x 0 ) = ⋯ = f ( n − 1 ) ( x 0 ) = 0 f^{\prime}\left(x_{0}\right)=f^{\prime \prime}\left(x_{0}\right)=\cdots=f^{(n-1)}\left(x_{0}\right)=0 f′(x0)=f′′(x0)=⋯=f(n−1)(x0)=0,但 f ( n ) ( x 0 ) ≠ 0 f^{(n)}\left(x_{0}\right) \neq0 f(n)(x0)=0,则
(1)当$ n 为偶数时 为偶数时 为偶数时{f(x)} 在 在 在x_{0}$处取得极值.其中当 f ( n ) ( x 0 ) > 0 f^{(n)}\left(x_{0}\right)>0 f(n)(x0)>0时取极小值,当 f ( n ) ( x 0 ) < 0 f^{(n)}\left(x_{0}\right)<0 f(n)(x0)<0 时取极大值
(2)当 n n n为奇数时 f ( x ) {f(x)} f(x)在 x 0 x_{0} x0处无极值
第二充分条件举例
lim x → x 0 + f ′ ( x 0 ) − f ′ ( x ) x − x 0 = f ′ ′ ( x 0 ) > 0 → f ′ ( x 0 ) > f ′ ( x ) 当 x → x 0 + lim x → x 0 − f ′ ( x 0 ) − f ′ ( x ) x − x 0 = f ′ ′ ( x 0 ) > 0 → f ′ ( x 0 ) < f ′ ( x ) 当 x → x 0 − ∵ 当 x → x 0 + 时 , f ′ ( x ) > 0 ; 当 x → x 0 − 时 , f ′ ( x ) < 0 ∴ f ( x 0 ) 为极小值 \begin{aligned} & \lim_{x \rightarrow x_0^+}\frac{f'(x_0)-f'(x)}{x-x_0} = f''(x_0) >0 \rightarrow f'(x_0)>f'(x) 当x \rightarrow x_0^+\\ & \lim_{x \rightarrow x_0^-}\frac{f'(x_0)-f'(x)}{x-x_0} = f''(x_0) >0 \rightarrow f'(x_0)
不可导点的四种情况
- 没有定义的点。 例如分母为0
- 不连续点/间断点
- 连续点但图像不光滑,尖点
- 斜率无限大点。例如垂直x轴
点可导的充要条件 左右导数存在且相等
【例题】2014数一
二 凹凸性
引理
根据图像,当二阶导数>0(增加得越来越快/减少得越来越慢),微分dy小于变化量Δy (单调减时dy负得多,单调增时dy正得少)
根据泰勒展开后还有一个关于二阶导数的高阶无穷小大于(小于)0也可以得出如下结论
f ′ ′ ( x ) > 0 → f ( x ) ≥ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 当且仅当 x = x 0 时等号成立 f ′ ′ ( x ) < 0 → f ( x ) ≤ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 当且仅当 x = x 0 时等号成立 f''(x)>0 \rightarrow f(x) \ge f(x_0)+f'(x_0)(x-x_0) \ 当且仅当x=x_0时等号成立 \\ f''(x)<0 \rightarrow f(x) \le f(x_0)+f'(x_0)(x-x_0) \ 当且仅当x=x_0时等号成立 f′′(x)>0→f(x)≥f(x0)+f′(x0)(x−x0) 当且仅当x=x0时等号成立f′′(x)<0→f(x)≤f(x0)+f′(x0)(x−x0) 当且仅当x=x0时等号成立
证明 (只证明第一个)
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( δ ) 2 ! ( x − x 0 ) 2 ∵ f ′ ′ ( x ) > 0 ∴ f ( x ) ≥ f ( x 0 ) + f ′ ( x ) ( x − x 0 ) 当且仅当 x = x 0 时等号成立 \begin{aligned} & f(x) = f(x_0)+f'(x_0)(x-x_0)+\frac{f''(\delta)}{2!}(x-x_0)^2 \\ & \because f''(x)>0 \\ & \therefore f(x) \ge f(x_0) + f'(x)(x-x_0) \\ & 当且仅当x=x_0时等号成立 \end{aligned} f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(δ)(x−x0)2∵f′′(x)>0∴f(x)≥f(x0)+f′(x)(x−x0)当且仅当x=x0时等号成立
2.1 定义
函数中点 与 函数值中点
拐点是一个坐标点而不单单是x的坐标
拐点表明该点左右两侧的图像凹凸性不同,不能单纯使用二阶导数为0作为判断条件因为还有可能不存在,关键看该点两侧的二阶导数是否异号。
在n阶可导点,极值点一定不是拐点,拐点也一定不是极值点。
在不可导点,我们可以构造出既是拐点又是极值点的函数。换句话说,如果一个点既是极值点,又是拐点,那么这个点一定不可导。
【例题】2015数一
2.2 判别法
思路:找二阶导数=0的点
凹: 二阶导数 > 0。一阶导数变大 => 增加变快/减少变慢 => 曲线有向上的趋势
凸: 二阶导数 < 0。一阶导数变小 = >增加变慢/减少变快 => 曲线有向下的趋势
充分条件
- f(x)三阶可导,若二阶导=0,且三阶导不为0,则是拐点【3阶导不为0则二阶导为0时左右异号】
- f(x)2n+1阶可导,若f(2n)=0,且2n+1阶导不为0,则是拐点
注意上面只是充分条件,当f(3)(x)=0时,不能得出一定不是拐点的结论,转为看2阶导是否异号。
【例题】2011数一
证明 凹 (需要使用到引理)
∵ f ′ ′ ( x ) > 0 ∴ f ( x ) ≥ f ( x 0 ) + f ′ ( x ) ( x − x 0 ) ∵ ∀ x 1 , x 2 ∈ [ a , b ] 且 x 1 ≠ x 2 , 取 x 1 + x 2 2 = x 0 ∴ 1 2 f ( x 1 ) > 1 2 f ( x 0 ) + f ′ ( x 0 ) 1 2 ( x 1 − x 0 ) 同理 1 2 f ( x 2 ) > 1 2 f ( x 0 ) + f ′ ( x 0 ) 1 2 ( x 2 − x 0 ) 两式相加得 1 2 f ( x 1 ) + f ( x 2 ) > f ( x 0 ) = f ( x 1 + x 2 2 ) ∴ f ( x 1 ) + f ( x 2 ) 2 > f ( x 1 + x 2 2 ) 成立 \begin{aligned} & \because f''(x)>0 \\ & \therefore f(x) \ge f(x_0)+f'(x_)(x-x_0) \\ & \because \forall x_1,x_2 \in [a,b] 且x_1 \neq x_2,取\frac{x_1+x_2}{2} = x_0 \\ & \therefore \frac{1}{2}f(x_1)\ > \frac{1}{2}f(x_0) + f'(x_0)\frac{1}{2}(x_1 - x_0) \\ & \ 同理 \frac{1}{2}f(x_2)\ > \frac{1}{2}f(x_0) + f'(x_0)\frac{1}{2}(x_2 - x_0) \\ & \ 两式相加得 \frac{1}{2}f(x_1)+f(x_2) > f(x_0) = f(\frac{x_1+x_2}{2}) \\ & \therefore \frac{f(x_1)+f(x_2)}{2} > f(\frac{x_1+x_2}{2}) \ 成立 \end{aligned} ∵f′′(x)>0∴f(x)≥f(x0)+f′(x)(x−x0)∵∀x1,x2∈[a,b]且x1=x2,取2x1+x2=x0∴21f(x1) >21f(x0)+f′(x0)21(x1−x0) 同理21f(x2) >21f(x0)+f′(x0)21(x2−x0) 两式相加得21f(x1)+f(x2)>f(x0)=f(2x1+x2)∴2f(x1)+f(x2)>f(2x1+x2) 成立
扩展
- 导数的意义 一阶斜率,二阶斜率的变化率,三阶凹凸变换趋势
- 多阶导数的几何意义
- 一阶:正表增,负表减
- 二阶:正,一阶导增,下凹;负,一阶导减,上凸
- 三阶:正,下凹越来越厉害,上凸越来越弱
- 物理意义
- 一阶 速度
- 二阶 加速度
- 三阶 加加速度/急动度/力变率
- 四阶 痉挛度
- 力变率反映人民的舒适程度,加速度/力恒定时候比力变换时候更舒适,人们看见速度感受加速度厌恶急动度
【例题】2014数一
三 渐近线
定义
曲线上一点M沿曲线无限远离原点或无限接近间断点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
可分为垂直渐近线、水平渐近线和斜渐近线。
3.1 水平渐近线
x = 无穷时,若$ \lim_{x \rightarrow ∞}f(x) = A$,称 y = A 为L:y=f(x)的水平渐近线。
函数图像可能没有水平渐近线,但是最多只有两条水平渐近线
3.2 铅直渐近线
不可导点 若 lim x → a f ( x ) = ∞ 或 f ( a ± 0 ) = ∞ 若 \lim_{x \rightarrow a} f(x) = ∞ 或 f(a±0)= ∞ 若limx→af(x)=∞或f(a±0)=∞,则称x = a为曲线y=f(x)的铅直渐近线
出现在函数无定义处,即间断点
若x=a是f(x)的铅直渐近线则x=a是y=f(x)的间断点,反之不一定。
3.3 斜渐近线
无穷点, 若 lim x → ∞ f ( x ) x = a ( ≠ 0 , ∞ ) , lim x → ∞ [ f ( x ) − a x ] = b 若\lim_{x \rightarrow ∞}\frac{f(x)}{x} = a(\neq 0,∞) ,\lim_{x \rightarrow ∞}[f(x) - ax] = b 若limx→∞xf(x)=a(=0,∞),limx→∞[f(x)−ax]=b,称y = ax + b 为y=f(x)的渐近线
选择题时,判断函数能否表达成 ax+b+o(x),可尝试泰勒。
【例题】
3.4 求法
首先我们注意到渐近线非为三种
- 铅直(x 间断点),就求得一个当趋于x的时,在该值处函数Y,趋于无穷则存在铅直渐近线
- 水平(x = ±无穷),就求得一个当x趋于无穷时函数值Y的极限,极限不存在就考虑 f(x)/x 看斜是否存在
- 斜渐近线,先判断比值 f(x)/x 极限k是否存在,若存在则有,再假设直线的截距b代入题中已知一般就能求出来了
然后,先找间断点判铅直,再令x为正负无穷,找水平/斜,注意一侧有水平则必无斜
注意
- 在一侧有水平渐近线则该侧不存在斜渐近线
- 若是偶函数,则斜渐进线也对称
- 水平最多两条,斜最多两条
- 有一些函数一眼可知不存在水平渐进线
【例题】
四 弧微分与曲率
弧微分
弧微分的基本公式: ( d s ) 2 = ( d x ) 2 + ( d y ) 2 (\mathrm{d} s)^{2}=(\mathrm{d} x)^{2}+(\mathrm{d} y)^{2} (ds)2=(dx)2+(dy)2,其中:
(1) 设 L : y = f ( x ) L: y={f(x)} L:y=f(x),则 d s = 1 + f ′ 2 ( x ) d x \mathrm{d} s=\sqrt{1+f^{\prime2}(x)} \mathrm{d} x ds=1+f′2(x)dx;
(2) 设 L : { x = φ ( t ) , y = ψ ( t ) , L:\left\{\begin{array}{l}x=\varphi(t), \\ y=\psi(t),\end{array}\right. L:{x=φ(t),y=ψ(t),则 d s = φ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \mathrm{d} s=\sqrt{\varphi^{\prime2}(t)+\psi^{\prime2}(t)} \mathrm{d} t ds=φ′2(t)+ψ′2(t)dt;
(3) 设 L : r = r ( θ ) L: r=r(\theta) L:r=r(θ),则 d s = r 2 ( θ ) + r ′ 2 ( θ ) d θ \mathrm{d} s=\sqrt{r^{2}(\theta)+r^{\prime2}(\theta)} \mathrm{d} \theta ds=r2(θ)+r′2(θ)dθ.
一些推导
( Δ s ) 2 = ( Δ x ) 2 + ( Δ y ) 2 ( d s ) 2 = ( d x ) 2 + ( d y ) 2 d s = ( d x ) 2 + ( d y ) 2 = 1 + ( d y d x ) 2 = 1 + f ′ 2 ( x ) d x \begin{aligned} & (Δs)^2 = (Δx)^2 + (Δy)^2 \\ & (ds)^2 = (dx)^2 + (dy)^2 \\ & \begin{aligned} ds = &\sqrt{(dx)^2+(dy)^2} \\ = &\sqrt{1 + (\frac{dy}{dx})^2} \\ = &\sqrt{1+f'^2(x)}dx \end{aligned} \end{aligned} (Δs)2=(Δx)2+(Δy)2(ds)2=(dx)2+(dy)2ds===(dx)2+(dy)21+(dxdy)21+f′2(x)dx
设L:r = r(θ)
x = r ( θ ) cos θ , ( d x ) 2 = ( r ′ cos − r sin ) 2 y = r ( θ ) sin θ , ( d y ) 2 = ( r ′ sin + r cos ) 2 d s = d ( x ) 2 + ( d y ) 2 = r 2 ( θ ) + r ′ 2 ( θ ) \begin{aligned} & x = r(\theta)\cos \theta,(dx)^2 = (r'\cos -r\sin)^2 \\ & y = r(\theta)\sin \theta,(dy)^2 = (r'\sin+r\cos)^2 \\ & ds = \sqrt{d(x)^2 + (dy)^2} = \sqrt{r^2(\theta) + r'^2(\theta)} \end{aligned} x=r(θ)cosθ,(dx)2=(r′cos−rsin)2y=r(θ)sinθ,(dy)2=(r′sin+rcos)2ds=d(x)2+(dy)2=r2(θ)+r′2(θ)
曲率
曲率计算公式: k = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 k=\frac{\left|y^{\prime \prime}\right|}{\left(1+y^{\prime2}\right)^{\frac{3}{2}}} k=(1+y′2)23∣y′′∣
曲率半径计算公式: R = 1 k R=\frac{1}{k} R=k1.
五 基础例题
点比较
包括:极值点,驻点(一阶导数=0),拐点(左右两侧凹凸性不同)
- 判大小
拐点
- 判断拐点与凹凸区间
渐近线
根与零点
存在性:零点定理、罗尔定理(F’ = f)
根个数:单调性(区间)、罗尔定理推论、找异号区间(0、±1、±2)
- 构造原函数
- 数形结合问题
不等式证明
难点
常见方法:中值定理,单调性,凹凸性,最值定理
- 中值定理
- 保号性的直接运用