线性代数的本质(十)——矩阵分解
文章目录
- 矩阵分解
-
- LU分解
- QR分解
- 特征值分解
- 奇异值分解
-
- 奇异值分解
- 矩阵的基本子空间
- 奇异值分解的性质
- 矩阵的外积展开式
矩阵分解
矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。
LU分解
设 A A A 是 m × n m\times n m×n 矩阵,若 A A A 可以写成乘积
A = L U A=LU A=LU
其中, L L L 为 m m m 阶下三角方阵,主对角线元素全是1。 U U U 为 A A A 得到一个行阶梯形矩阵。这样一个分解称为LU分解。 L L L 称为单位下三角方阵。
我们先来看看,LU分解的一个应用。当 A = L U A=LU A=LU 时,方程 A x = b A\mathbf x=\mathbf b Ax=b 可写成 L ( U x ) = b L(U\mathbf x)=\mathbf b L(Ux)=b,于是分解为下面两个方程
L y = b U x = y L\mathbf y=\mathbf b \\ U\mathbf x=\mathbf y Ly=bUx=y
因为 L L L 和 U U U 都是三角矩阵,每个方程都比较容易解。
LU 分解算法:本节只讲述仅用行倍加变换求解。可以证明,单位下三角矩阵的乘积和逆也是单位下三角矩阵 。此时,可以用行倍加变换寻找 L L L 和 U U U 。假设存在单位下三角初等矩阵 P 1 , ⋯ , P s P_1,\cdots,P_s P1,⋯,Ps 使
P 1 ⋯ P s A = U P_1\cdots P_sA=U P1⋯PsA=U
于是便得到了 U U U 和 L L L
L = ( P 1 , ⋯ , P s ) − 1 L=(P_1,\cdots,P_s)^{-1} L=(P1,⋯,Ps)−1
QR分解
如果 m × n m\times n m×n 矩阵 A A A 的列向量线性无关,那么 A A A 可以分解为 A = Q R A=QR A=QR,其中 Q Q Q 是一个 m × n m\times n m×n 正交矩阵,其列为 col A \text{col }A col A 的一组标准正交基, R R R 是一个上 n × n n\times n n×n 三角可逆矩阵,且其对角线上的元素全为正数。
证:矩阵 A = ( x 1 , x 2 , ⋯ , x n ) A=(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n) A=(x1,x2,⋯,xn) 的列向量是 col A \text{col }A col A 的一组基,使用施密特正交化方法可以构造一组标准正交基 u 1 , u 2 , ⋯ , u n \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n u1,u2,⋯,un ,取
Q = ( u 1 , u 2 , ⋯ , u n ) Q=(\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n) Q=(u1,u2,⋯,un)
因为在正交化过程中 x k ∈ span { x 1 , ⋯ , x k } = span { u 1 , ⋯ , u k } , k = 1 , 2 , ⋯ , n \mathbf x_k\in\text{span}\{\mathbf x_1,\cdots,\mathbf x_k\}=\text{span}\{\mathbf u_1,\cdots,\mathbf u_k\},\quad k=1,2,\cdots,n xk∈span{x1,⋯,xk}=span{u1,⋯,uk},k=1,2,⋯,n 。所以 x k \mathbf x_k xk 可线性表示为
x k = r 1 k u 1 + ⋯ + r k k u k + 0 ⋅ u k + 1 + ⋯ + 0 ⋅ u n \mathbf x_k=r_{1k}\mathbf u_1+\cdots+r_{kk}\mathbf u_k+0\cdot\mathbf u_{k+1}+\cdots+0\cdot\mathbf u_n xk=r1ku1+⋯+rkkuk+0⋅uk+1+⋯+0⋅un
于是
x k = Q r k \mathbf x_k=Q\mathbf r_k xk=Qrk
其中 r k = ( r 1 k , ⋯ , r k k , 0 , ⋯ , 0 ) T \mathbf r_k=(r_{1k},\cdots,r_{kk},0,\cdots,0)^T rk=(r1k,⋯,rkk,0,⋯,0)T ,且 r k k ⩾ 0 r_{kk}\geqslant 0 rkk⩾0 (在正交化过程中,若 r k k < 0 r_{kk}<0 rkk<0 ,则 r k k r_{kk} rkk 和 u k \mathbf u_k uk 同乘-1)。取 R = ( r 1 , r 2 , ⋯ , r n ) R=(\mathbf r_1,\mathbf r_2,\cdots,\mathbf r_n) R=(r1,r2,⋯,rn) ,则
A = ( Q r 1 , Q r 2 , ⋯ , Q r n ) = Q R A=(Q\mathbf r_1,Q\mathbf r_2,\cdots,Q\mathbf r_n)=QR A=(Qr1,Qr2,⋯,Qrn)=QR
例:求 A = [ 1 0 0 1 1 0 1 1 1 1 1 1 ] A=\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix} A= 111101110011 的一个 QR 分解
解:通过施密特正交化方法我们可以得到 col A \text{col }A col A 的一组标准正交基,将这些向量组成矩阵
Q = [ 1 / 2 − 3 / 12 0 1 / 2 1 / 12 − 2 / 6 1 / 2 1 / 12 1 / 6 1 / 2 1 / 12 1 / 6 ] Q=\begin{bmatrix}1/2&-3/\sqrt{12}&0\\1/2&1/\sqrt{12}&-2/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\end{bmatrix} Q= 1/21/21/21/2−3/121/121/121/120−2/61/61/6
注意到 Q Q Q 是正交矩阵, Q T = Q − 1 Q^T=Q^{-1} QT=Q−1 。所以 R = Q − 1 A = Q T A R=Q^{-1}A=Q^TA R=Q−1A=QTA
R = [ 1 / 2 1 / 2 1 / 2 1 / 2 − 3 / 12 1 / 12 1 / 12 1 / 12 0 − 2 / 6 1 / 6 1 / 6 ] [ 1 0 0 1 1 0 1 1 1 1 1 1 ] = [ 2 3 / 2 1 0 3 / 12 2 / 12 0 0 2 / 6 ] R=\begin{bmatrix}1/2&1/2&1/2&1/2\\ -3/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12} \\ 0&-2/\sqrt{6}&1/\sqrt{6}&1/\sqrt{6} \end{bmatrix} \begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix}= \begin{bmatrix}2&3/2&1\\0&3/\sqrt{12}&2/\sqrt{12}\\0&0&2/\sqrt{6} \end{bmatrix} R= 1/2−3/1201/21/12−2/61/21/121/61/21/121/6 111101110011 = 2003/23/12012/122/6
特征值分解
特征值分解是将矩阵分解成特征值和特征向量形式:
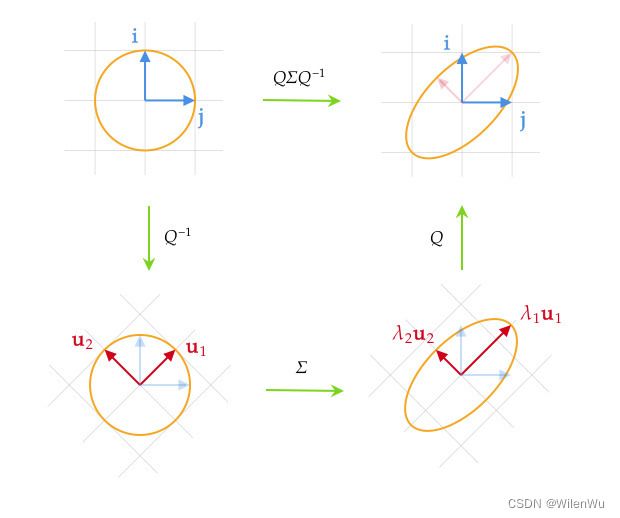
A = Q Σ Q − 1 A=Q\Sigma Q^{-1} A=QΣQ−1
其中, Σ = diag ( λ 1 , λ 2 , ⋯ , λ n ) \Sigma=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n) Σ=diag(λ1,λ2,⋯,λn) 是一个对角阵,其对角线元素是矩阵 A A A 的特征值按降序排列 λ 1 ⩾ λ 2 ⩾ ⋯ ⩾ λ n \lambda_1\geqslant\lambda_2\geqslant\cdots\geqslant\lambda_n λ1⩾λ2⩾⋯⩾λn, Q = ( u 1 , u 2 , … , u n ) Q=(\mathbf u_1,\mathbf u_2,\dots,\mathbf u_n) Q=(u1,u2,…,un) 是特征值对应的特征向量组成的矩阵。
特征值分解后,方阵的幂变得更容易计算
A t = Q Σ t Q − 1 = Q [ λ 1 t ⋱ λ n t ] Q − 1 A^t=Q\Sigma^t Q^{-1}=Q\begin{bmatrix}\lambda_1^t\\&\ddots\\&&\lambda_n^t\end{bmatrix}Q^{-1} At=QΣtQ−1=Q λ1t⋱λnt Q−1
特征值分解可以理解为:先切换基向量,然后伸缩变换,最后再切换回原来的基向量。其中, Σ \Sigma Σ 中的特征向量描述伸缩变换的程度,特征向量描述变换的方向。
特征值分解有一定的局限性,因为它只适用于满秩的方阵。
例:求矩阵 A = [ − 2 1 1 0 2 0 − 4 1 3 ] A=\begin{bmatrix}-2&1&1\\0&2&0\\-4&1&3\end{bmatrix} A= −20−4121103 的特征值分解。
解:矩阵 A A A 的特征多项式为 det ( A − λ I ) = − ( λ − 2 ) 2 ( λ + 1 ) \det(A-\lambda I)=-(\lambda-2)^2(\lambda+1) det(A−λI)=−(λ−2)2(λ+1) 。特征值和特征向量分别为
λ 1 = − 1 : u 1 = [ 1 0 1 ] ; λ 2 = 2 : u 2 = [ 0 1 − 1 ] , u 3 = [ 1 0 4 ] \lambda_1=-1:\mathbf u_1=\begin{bmatrix}1\\0\\1\end{bmatrix};\quad \lambda_2=2:\mathbf u_2=\begin{bmatrix}0\\1\\-1\end{bmatrix}, \mathbf u_3=\begin{bmatrix}1\\0\\4\end{bmatrix} λ1=−1:u1= 101 ;λ2=2:u2= 01−1 ,u3= 104
可通过行变换计算逆矩阵
( Q , I ) = [ 0 1 1 1 0 0 1 0 0 0 1 0 − 1 4 1 0 0 1 ] → [ 1 0 0 0 1 0 0 1 0 − 1 / 3 1 / 3 1 / 3 0 0 1 4 / 3 − 1 / 3 − 1 / 3 ] = ( I , Q − 1 ) (Q,I)=\begin{bmatrix}\begin{array}{ccc:ccc} 0&1&1&1&0&0\\1&0&0&0&1&0\\-1&4&1&0&0&1 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:ccc} 1&0&0&0&1&0\\0&1&0&-1/3&1/3&1/3\\0&0&1&4/3&-1/3&-1/3 \end{array}\end{bmatrix}=(I,Q^{-1}) (Q,I)= 01−1104101100010001 → 1000100010−1/34/311/3−1/301/3−1/3 =(I,Q−1)
所以
A = [ 0 1 1 1 0 0 − 1 4 1 ] [ 2 0 0 0 2 0 0 0 − 1 ] [ 0 1 0 − 1 / 3 1 / 3 1 / 3 4 / 3 − 1 / 3 − 1 / 3 ] A=\begin{bmatrix}0&1&1\\1&0&0\\-1&4&1\end{bmatrix} \begin{bmatrix}2&0&0\\0&2&0\\0&0&-1\end{bmatrix} \begin{bmatrix}0&1&0\\-1/3&1/3&1/3\\4/3&-1/3&-1/3\end{bmatrix} A= 01−1104101 20002000−1 0−1/34/311/3−1/301/3−1/3
奇异值分解
奇异值分解
奇异值分解(Singular Value Decomposition, SVD)是线性代数中一种重要的矩阵分解,在生物信息学、信号处理、金融学、统计学等领域有重要应用。
SVD 可以理解为同一线性变换 T : R n ↦ R m T:\R^n\mapsto\R^m T:Rn↦Rm 在不同基下的矩阵表示。假设 Grant 选用标准基,对应的矩阵为 A m × n A_{m\times n} Am×n 。类似于特征值分解, Jennifer 通过选择合适的基向量,对应的矩阵变为简单的长方形对角矩阵 Σ m × n \Sigma_{m\times n} Σm×n,即只有伸缩变换。
假定 Jennifer 使用矩阵 V n = ( v 1 , ⋯ , v n ) V_n=(\mathbf v_1,\cdots,\mathbf v_n) Vn=(v1,⋯,vn) 的列向量作为 R n R^n Rn 的基,使用矩阵 U n = ( u 1 , ⋯ , u m ) U_n=(\mathbf u_1,\cdots,\mathbf u_m) Un=(u1,⋯,um)的列向量作为 R m R^m Rm 的基 。那么,对于 Jennifer 视角下的向量 x ∈ R n \mathbf x\in R^n x∈Rn
- 同样的向量,用 Grant 的坐标系表示为 V x V\mathbf x Vx
- 用 Grant 的语言描述变换后的向量 A V x AV\mathbf x AVx
- 将变换后的结果变回 Jennifer 的坐标系 U − 1 A V x U^{-1}AV\mathbf x U−1AVx
于是,我们得到同一个线性变换 T T T 在 Jennifer 的坐标系下对应的矩阵 Σ = U − 1 A V \Sigma=U^{-1}AV Σ=U−1AV ,也可理解为矩阵 A A A 分解为 A m × n = U m Σ m × n V n − 1 A_{m\times n}=U_m\Sigma_{m\times n}V^{-1}_n Am×n=UmΣm×nVn−1 。
接下来,自然是探讨上述矩阵分解的适用条件。
注意到
A T A = ( U Σ V − 1 ) T ( U Σ V − 1 ) = V − T Σ T U T U Σ V − 1 A^TA=(U\Sigma V^{-1})^T(U\Sigma V^{-1})=V^{-T}\Sigma^TU^TU\Sigma V^{-1} ATA=(UΣV−1)T(UΣV−1)=V−TΣTUTUΣV−1
不妨取 U , V U,V U,V 为单位正交基,即 U , V U,V U,V 为正交矩阵 U T U = I , V T V = I U^TU=I,V^TV=I UTU=I,VTV=I ,则
A T A = V Σ T Σ V T A^TA=V\Sigma^T\Sigma V^T ATA=VΣTΣVT
于是,可知 V V V 的列向量为 A T A A^TA ATA 的特征向量, Σ T Σ \Sigma^T\Sigma ΣTΣ 为 n n n 阶对角阵,其对角元素为 A T A A^TA ATA 的特征值。事实上 A T A A^TA ATA 为对称阵,必定存在正交矩阵 V V V 相似对角化。
同理
A A T = U Σ Σ T U T AA^T=U\Sigma\Sigma^T U^T AAT=UΣΣTUT
可知 U U U 的列向量为 A A T AA^T AAT 的特征向量, Σ Σ T \Sigma\Sigma^T ΣΣT 为 m m m 阶对角阵,其对角元素为 A A T AA^T AAT 的特征值。矩阵 A T A A^TA ATA 为对称阵,必定存在正交矩阵 U U U 相似对角化。
目前 U , V U,V U,V 我们都求出来了,只剩下求出长方形对角矩阵 Σ \Sigma Σ 。根据 Sylvester降幂公式, A T A A^TA ATA 和 A A T AA^T AAT 有相同的非零特征值。
令 Σ = [ Λ r O O O ] \Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix} Σ=[ΛrOOO] ,其中 Λ r = diag ( σ 1 , ⋯ , σ r ) \Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r) Λr=diag(σ1,⋯,σr) 。则
Σ T Σ = [ Λ r 2 O O O ] n , Σ Σ T = [ Λ r 2 O O O ] m \Sigma^T\Sigma=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_n,\quad \Sigma\Sigma^T=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_m ΣTΣ=[Λr2OOO]n,ΣΣT=[Λr2OOO]m
其中 Λ r 2 = diag ( σ 1 2 , ⋯ , σ r 2 ) \Lambda_r^2=\text{diag}(\sigma_1^2,\cdots,\sigma_r^2) Λr2=diag(σ12,⋯,σr2) 。因此,矩阵 Σ \Sigma Σ 的对角元素是 A T A A^TA ATA 和 A A T AA^T AAT 的特征值 λ j \lambda_j λj 的平方根
σ j = λ j \sigma_j=\sqrt{\lambda_j} σj=λj
综上,任意矩阵均可奇异值分解。
定义:SVD是指将秩为 r r r 的 m × n m\times n m×n 矩阵 A A A分解为
A = U Σ V T A=U\Sigma V^T A=UΣVT
其中 U U U 为 m m m 阶正交阵, V V V 为 n n n 阶正交阵, Σ \Sigma Σ 为 m × n m\times n m×n 维长方形对角矩阵,对角元素称为矩阵 A A A 的奇异值,一般按降序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 ,这样 Σ \Sigma Σ 就唯一确定了。矩阵 U U U 的列向量称为左奇异向量(left singular vector),矩阵 V V V 的列向量称为右奇异向量(right singular vector)。

例:这里我们用一个简单的矩阵来说明奇异值分解的步骤。求矩阵 A = [ 0 1 1 1 1 0 ] A=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} A= 011110 的奇异值分解
解:首先求出对称阵 A T A A^TA ATA 和 A A T AA^T AAT
A T A = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 2 1 1 2 ] A A T = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 1 1 0 1 2 1 0 1 1 ] A^TA=\begin{bmatrix}0&1&1\\1&1&0\end{bmatrix} \begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix}= \begin{bmatrix}2&1\\1&2\end{bmatrix} \\ AA^T=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} \begin{bmatrix}0&1&1\\1&1&0\end{bmatrix}= \begin{bmatrix}1&1&0\\1&2&1\\0&1&1\end{bmatrix} ATA=[011110] 011110 =[2112]AAT= 011110 [011110]= 110121011
然后求出 A T A A^TA ATA 的特征值和特征向量
λ 1 = 3 : v 1 = [ 1 / 2 1 / 2 ] ; λ 2 = 1 : v 2 = [ − 1 / 2 1 / 2 ] \lambda_1=3:\mathbf v_1=\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix};\quad \lambda_2=1:\mathbf v_2=\begin{bmatrix}-1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix} λ1=3:v1=[1/21/2];λ2=1:v2=[−1/21/2]
求出 A A T AA^T AAT 的特征值和特征向量
λ 1 = 3 : u 1 = [ 1 / 6 2 / 6 1 / 6 ] ; λ 2 = 1 : u 2 = [ 1 / 2 0 − 1 / 2 ] ; λ 3 = 0 : u 3 = [ 1 / 3 − 1 / 3 1 / 3 ] ; \lambda_1=3:\mathbf u_1=\begin{bmatrix}1/\sqrt{6}\\2/\sqrt{6}\\1/\sqrt{6}\end{bmatrix};\quad \lambda_2=1:\mathbf u_2=\begin{bmatrix}1/\sqrt{2}\\0\\-1/\sqrt{2}\end{bmatrix};\quad \lambda_3=0:\mathbf u_3=\begin{bmatrix}1/\sqrt{3}\\-1/\sqrt{3}\\1/\sqrt{3}\end{bmatrix}; λ1=3:u1= 1/62/61/6 ;λ2=1:u2= 1/20−1/2 ;λ3=0:u3= 1/3−1/31/3 ;
其次可以利用 σ i = λ i \sigma_i=\sqrt{\lambda_i} σi=λi 求出奇异值 3 , 1 \sqrt{3},1 3,1
最终得到 A A A的奇异值分解
A = U Σ V T = [ 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ] [ 3 0 0 1 0 0 ] [ 1 / 2 1 / 2 − 1 / 2 1 / 2 ] A=U\Sigma V^T=\begin{bmatrix}1/\sqrt{6}&1/\sqrt{2}&1/\sqrt{3}\\2/\sqrt{6}&0&-1/\sqrt{3}\\1/\sqrt{6}&-1/\sqrt{2}&1/\sqrt{3}\end{bmatrix} \begin{bmatrix}\sqrt{3}&0\\0&1\\0&0\end{bmatrix} \begin{bmatrix}1/\sqrt{2}&1/\sqrt{2}\\-1/\sqrt{2}&1/\sqrt{2}\end{bmatrix} A=UΣVT= 1/62/61/61/20−1/21/3−1/31/3 300010 [1/2−1/21/21/2]
矩阵的基本子空间
设矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT ,有 r r r 个不为零的奇异值,则可以得到矩阵 A A A 的四个基本子空间:
- 正交阵 U U U 的前 r r r 列是 col A \text{col }A col A 的一组单位正交基
- 正交阵 U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基
- 正交阵 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基
- 正交阵 V V V 的后 n − r n-r n−r 列是 ker A \ker A kerA 的一组单位正交基
A ( v 1 , ⋯ , v r ⏟ col A T , v r + 1 ⋯ v n ⏟ ker A ) = ( u 1 , ⋯ , u r ⏟ col A , u r + 1 ⋯ u m ⏟ ker A T ) [ σ 1 ⋱ σ r O ] ⏟ Σ m × n A(\underbrace{\mathbf v_1,\cdots,\mathbf v_r}_{\text{col }A^T},\underbrace{\mathbf v_{r+1}\cdots\mathbf v_n}_{\ker A})= (\underbrace{\mathbf u_1,\cdots,\mathbf u_r}_{\text{col }A},\underbrace{\mathbf u_{r+1}\cdots\mathbf u_m}_{\ker A^T}) \underbrace{\begin{bmatrix}\sigma_1\\&\ddots\\&&\sigma_r\\&&&O \end{bmatrix}}_{\Sigma_{m\times n}} A(col AT v1,⋯,vr,kerA vr+1⋯vn)=(col A u1,⋯,ur,kerAT ur+1⋯um)Σm×n σ1⋱σrO
证:易知 A V = U Σ AV=U\Sigma AV=UΣ ,即
{ A v i = σ i u i , 1 ⩽ i ⩽ r A v i = 0 , r < i ⩽ n \begin{cases} A\mathbf v_i=\sigma_i\mathbf u_i, &1\leqslant i\leqslant r \\ A\mathbf v_i=0, &r< i\leqslant n \end{cases} {Avi=σiui,Avi=0,1⩽i⩽rr<i⩽n
取 v 1 , ⋯ , v n \mathbf v_1,\cdots,\mathbf v_n v1,⋯,vn 为 R n \R^n Rn 的单位正交基,对于 ∀ x ∈ R n \forall\mathbf x\in \R^n ∀x∈Rn ,可以写出 x = c 1 v 1 + ⋯ + c n v n \mathbf x=c_1\mathbf v_1+\cdots+c_n\mathbf v_n x=c1v1+⋯+cnvn,于是
A x = c 1 A v 1 + ⋯ + c r A v r + c r + 1 A v r + 1 + ⋯ + c n v n = c 1 σ 1 u 1 + ⋯ + c r σ 1 u r + 0 + ⋯ + 0 \begin{aligned} A\mathbf x&=c_1A\mathbf v_1+\cdots+c_rA\mathbf v_r+c_{r+1}A\mathbf v_{r+1}+\cdots+c_n\mathbf v_n \\ &=c_1\sigma_1\mathbf u_1+\cdots+c_r\sigma_1\mathbf u_r+0+\cdots+0 \end{aligned} Ax=c1Av1+⋯+crAvr+cr+1Avr+1+⋯+cnvn=c1σ1u1+⋯+crσ1ur+0+⋯+0
所以 A x ∈ span { u 1 , ⋯ , u r } A\mathbf x\in\text{span}\{\mathbf u_1,\cdots,\mathbf u_r\} Ax∈span{u1,⋯,ur} ,这说明矩阵 U U U 的前 r r r 列是 col A \text{col }A col A 的一组单位正交基,因此 rank A = r \text{rank }A=r rank A=r 。同时可知,对于任意的 x ∈ span { v r + 1 , ⋯ , v n } ⟺ A x = 0 \mathbf x\in\text{span}\{\mathbf v_{r+1},\cdots,\mathbf v_n\}\iff A\mathbf x=0 x∈span{vr+1,⋯,vn}⟺Ax=0 ,于是 V V V 的后 n − r n-r n−r 列是 ker A \ker A kerA 的一组单位正交基。
同样通过 A T U = V Σ A^TU=V\Sigma ATU=VΣ 可说明 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基, U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基。
奇异值分解的性质
设矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT ,秩 rank A = r \text{rank }A=r rank A=r ,分别将 U , Σ , V U,\Sigma,V U,Σ,V 进行分块
U = ( U r , U m − r ) V = ( V r , V n − r ) Σ = [ Λ r O O O ] U=(U_r,U_{m-r}) \\ V=(V_r,V_{n-r}) \\ \Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix} U=(Ur,Um−r)V=(Vr,Vn−r)Σ=[ΛrOOO]
其中 U r = ( u 1 , ⋯ , u r ) U_r=(\mathbf u_1,\cdots,\mathbf u_r) Ur=(u1,⋯,ur) 为 m × r m\times r m×r维矩阵, V r = ( v 1 , ⋯ , v r ) V_r=(\mathbf v_1,\cdots,\mathbf v_r) Vr=(v1,⋯,vr) 为 n × r n\times r n×r维矩阵, Λ r = diag ( σ 1 , ⋯ , σ r ) \Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r) Λr=diag(σ1,⋯,σr) 为 r r r 阶对角阵。应用矩阵乘法的性质,奇异值分解可以简化为
A = U r Λ r V r T A=U_r\Lambda_r V^T_r A=UrΛrVrT
这个分解称为简化奇异值分解。
性质:
- 奇异值分解可理解为将线性变换分解为三个简单的变换:正交变换 V T V^T VT,伸缩变换 Σ \Sigma Σ 和正交变换 U U U 。
- 矩阵 A A A 的奇异值分解中,奇异值是唯一的,但矩阵 U , V U,V U,V 不是唯一的。
- 令 λ \lambda λ 为 A T A A^TA ATA 的一个特征值, v \mathbf v v 是对应的特征向量,则
∥ A v ∥ 2 = v T A T A v = λ v T v = λ ∥ v ∥ \|A\mathbf v\|^2=\mathbf v^TA^TA\mathbf v=\lambda\mathbf v^T\mathbf v=\lambda\|\mathbf v\| ∥Av∥2=vTATAv=λvTv=λ∥v∥ - 易知 A V = U Σ AV=U\Sigma AV=UΣ 或 A T U = V Σ T A^TU=V\Sigma^T ATU=VΣT,则左奇异向量和右奇异向量存在关系
A v j = σ j u j A T u j = σ j v j A\mathbf v_j=\sigma_j\mathbf u_j \\ A^T\mathbf u_j=\sigma_j\mathbf v_j Avj=σjujATuj=σjvj
矩阵的外积展开式
矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT 可展开为若干个秩为1的 m × n m\times n m×n矩阵之和
A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ r u r v r T A=\sigma_1\mathbf u_1\mathbf v_1^T+\sigma_2\mathbf u_2\mathbf v_2^T+\cdots+\sigma_r\mathbf u_r\mathbf v_r^T A=σ1u1v1T+σ2u2v2T+⋯+σrurvrT
上式称为矩阵 A A A 的外积展开式。
在长方形对角矩阵 Σ \Sigma Σ 中奇异值按从大到小的顺序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 。在很多情况下,由于奇异值递减很快,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上。因此,我们可以用前面 k k k 个大的奇异值来近似描述矩阵。
奇异值分解也是一种矩阵近似的方法,这个近似是在矩阵范数意义下的近似。矩阵范数是向量范数的直接推广。
∥ A ∥ 2 = ( ∑ j = 1 n ∑ i = 1 m ∣ a i j ∣ 2 ) 1 / 2 \|A\|_2=(\sum_{j=1}^{n}\sum_{i=1}^{m} |a_{ij}|^2)^{1/2} ∥A∥2=(j=1∑ni=1∑m∣aij∣2)1/2
可以证明
∥ A ∥ 2 2 = tr ( A T A ) = ∑ i = 1 r σ i 2 \|A\|_2^2=\text{tr}(A^TA)= \sum_{i=1}^{r} \sigma_i^2 ∥A∥22=tr(ATA)=i=1∑rσi2
设矩阵
A k = ∑ i = 1 k σ i u i v i T A_k=\sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T Ak=i=1∑kσiuiviT
则 A k A_k Ak 的秩为 k k k ,矩阵 A k A_k Ak 称为 A A A 的截断奇异值分解。并且 A k A_k Ak 是秩为 k k k 时的最优近似,即 A k A_k Ak 为以下最优问题的解
min ∥ A − X ∥ 2 s.t. rank A = k \min\|A-X\|_2 \\ \text{s.t. rank }A=k min∥A−X∥2s.t. rank A=k
上式称为低秩近似(low-rank approximation)。于是奇异值分解可近似为
A ≈ ∑ i = 1 k σ i u i v i T = U m × k Σ k × k V n × k T A\approx \sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T=U_{m\times k}\Sigma_{k\times k}V_{n\times k}^T A≈i=1∑kσiuiviT=Um×kΣk×kVn×kT
其中 k k k 是一个远远小于 m m m和 n n n的数,从计算机内存的角度来说,矩阵左(右)奇异向量和奇异值的存储要远远小于矩阵 A A A的。所以,截断奇异值分解就是在计算精度和时间空间之间做选择。如果 k k k越大,右边的三个矩阵相乘的结果越接近于 A A A。
截断奇异值分解常用于图像压缩,如下图